Практикум по высшей математике_часть 2

Уравнение Бернулли
Дифференциальное уравнение вида
y′+ P(x) y = Q(x) yn , n ≠ 0, n ≠1	(7.23)

называется уравнением Бернулли.

Уравнение Бернулли может быть сведено к линейному дифференциальному уравнению первого порядка. Для этого обе части уравнения (7.23) сначала

делят на yn . После этого вводят новую переменную z( y) = y1−n . В результате указанных преобразований уравнение (7.23) принимает следующий вид:

1 −z′n + P(x)z = Q(x) .

Заметим, что решение уравнения (7.23) можно искать в виде произведения двух функций y = uv , как и в случае решения линейных уравнений (метод

Бернулли) или методом вариации постоянной.

Примеры решения задач

Пример 7.12. Найти частное решение дифференциального уравнения y′− ytgx + y2 cos x = 0 , удовлетворяющее начальному условию y(0) = 13 .

Решение. Заданное дифференциальное уравнение является уравнением Бернулли. Найдем сначала общее решение данного уравнения, для этого разде-

лим обе его части на y2 :

yy2′ − tgyx + cos x = 0 .

Теперь вводим новую переменную z = y1−2 =					1	. Тогда	y = 1z , y′ = −	z′	и
					y			z2
уравнение принимает вид
−	z′	z	2	− ztgx + cos x = 0
	z2
или
z′+ ztgx = cos x .							(7.24)

158

Последнее уравнение есть линейное дифференциальное уравнение. Решаем его, используя метод замены. Пусть z = uv , z =u′v +uv′, тогда уравнение (7.24) перепишем в виде

′	′			′	′	= cos x .
u v +uv +uvtgx			= cos x или u v +u (v + vtgx)
	′	+ vtgx = 0 :
Решаем уравнение v
dv	= −vtgx ,	dv	= −tgxdx ,	∫dv	= −∫tgxdx , ln | v |= ln | cos x | .
dx		v		v
Отсюда v = cos x . Тогда для функции u(x) получаем
u′cos x = cos x ,			du = dx ,	u = x +C .

Следовательно, z = (x +C )cos x . Возвращаемся к исходной переменной:

	yо. р. =	1	=	1	или y(x +C )=	1	.
		z		(x +C )cos x		cos x

Заметим, что y = 0 также является решением исходного уравнения. Используя начальное условие, находим значение константы С:

1		1		1	1		С = 3.
3	=			3	=
		(0 +C )cos0				C

Следовательно, частное решение заданного дифференциального уравне-

ния, удовлетворяющее начальному условию y(0) = 13 , имеет вид:

yч. р. =	1	.
	(x +3)cos x

Пример 7.13. Найти общее решение уравнения xy′+ y = xy2 ln x . Решение. Находим решение данного уравнения Бернулли в виде y = uv ,

не приводя его к линейному уравнению. Тогда
′	′		= x(uv)	2	ln x	′	′	+ v)= x(uv)		2	ln x .
x(u v +uv )+uv						или xu v +u (xv
Находим функцию v(x) :
′		xdv		dv		dx			1
xv + v = 0 ,		dx	= −v ,	v = −		x , ln | v |= −ln | x |,			v = x .

159

Тогда для функции u(x) получаем уравнение u′ = u2v ln x , решая которое, находим

u

′

= u

2 ln x

,

du

= u

2 ln x

,

du

=

ln x

dx ,

x

dx

x

u2

x

du

=

ln x

dx ,

−

1

=

1

,

−

1

=

ln2 x

+C1 .

∫u

2

∫ x

u

∫

ln xd

u

2

x

Отсюда u = −ln2 x2+C , C = 2C1 . Следовательно, общее решение исходно-

го дифференциального уравнения:

y = −1			2		или xy(ln2 x +C )+ 2 = 0
	ln	2	x +C
x
Пример 7.14. Найти общее решение уравнения xy′+ y = 2x2 yy′ln y .
Решение. Так как y′x					1		, то, разделив данное уравнение на y′x , по-
					=
						′
						xy
				′	+ x = 2x			2	y ln y .
лучаем линейное уравнение yx

Решим последнее уравнение методом вариации постоянной. Для этого сначала находим решение соответствующего однородного уравнения:

′

dx

dx

dy

C

C

yx

+ x = 0 ,

y dy

= −x ,

x

= −

y

,

ln | x |= ln

y

,

x =

y .

Теперь, предполагая, что C = C( y) , подставляем найденное решение однородного уравнения в исходное уравнение.

С

′

С

2

′

−2

C

+ С

= 2С

2

y

+ x = 2

y ln y ,

y Сy

ln y ,

y

y

y

y

y

′

2

dC

2

dC

ln y

Сy = 2С

ln y ,

dy y

= 2С

ln y ,

С2

= 2

dy ,

y

dC

ln y

1

2

1

∫С2

= 2∫

y

dy, −

= ln

y +C0 , C( y) = −

.

C

ln2 y +C

0

Так как x = C( y)

, то общее решение исходного уравнения имеет вид

y

xy = −

1

или

xy (ln2 y +C0 )+1 = 0 .

ln

2

y +C

0

160

Задания для самостоятельного решения

7.1. Проверить, удовлетворяют ли дифференциальным уравнениям дан-

ные функции:

1)

x + y′ = 3x ,

y = x2 ;

2)

y′+ y cos x +sin 2x = 0 , y = cos x ;

y′′

+ x

2

2 y

4

′′

′

−2 x

y = x ;

y

+ 4 y

+5y = e sin x .

3)

12

= x

2

,

4)

7.2. Найти общие интегралы или общие решения дифференциальных

уравнений:
1)	xyy′ =1 − x2 ;													2)		xy′− y = 0 ;
3)	xy′− y = y3 ;													4)		ln | cos x | y′− ytgx = 0 ;
5)	(xy2 + x)dx + ( y − x2 y)dy = 0 ;													6)	y − xy′ = a(1 + x2 y′);
7)	ex2 dy +3x2 1 − y2 dx = 0 ;													8)	y2 y′ =1 − 2x ;
9)	tgxsin				2		ydx + cos			2	xctg ydy = 0 ;			10)			′
																	y tgx − y = a ;
11)		x3 y′ = 2 y ;												12)			y2dx −(2xy + 3)dy = 0 ;
		y	′				x + y					x − y					y
13)				+sin			2	=sin			2		;	14)			y′ = ln y ;
15)	(1 + x) ydx + (1 − y)xdy = 0 ;													16)			y′ = ytgx + cos x ;
17)	1 + y2					=1 + x		2	;					18)		(1 + 2x			2	) ydx + (1 + y)xdy = 0 ;
				y′
									1 + y2 sin y − xy)dy ;
19)	(1 + y2 )dx = (													20)			y′ = 52 x+y .

7.3. Найти частное решение дифференциального уравнения, удовлетворяющее начальному условию:

1)	y′sin x = y ln y, y0 = e, x0				= π		;
2) (1 + e2 x ) y2dy −exdx = 0, y						2
					0	= 0, x = 0 ;
							0
3)	y′−	1 + y2		= 0, y0 =1, x0 = 0 ;
		1	+ x2

4) 2 y′ x = y, y0 =1, x0 = 4 ; 5) e−y (1 + y′)=1, y0 =1, x0 =1;

6)	y−3 ln ln xdx + xey2 dy = 0,	y	0	= 0,			x = e ;
							0
7)	y′sin y cos x =sin xcos y,	y0		=	π	,	x0 = 0 .
					4

161

7.4.Найти общие или частные решения дифференциальных уравнений:

	y′−	x − y
1)			= 0 ;
		x − 2 y
2)	xy′− y = x2 + y2 ;
3)	y2 + x2 y = xyy′, y0 =1, x0 =1;

4)y′− x22+xyy2 = 0 ;

5)xy′+ y ln y −1 = 0 ;

x

6)

(xy′− y)arctg

y

= x,

y0 =1, x0 =1;

x

7)

xy′ = y + xsin

y

,

y0

=

π

, x0 =1;

x

2

y

y

xy′cos

8)

= y cos

− x ;

x

x

9)	xdy − ydx = x2 + y					2 dx y = 0,	x =1;
						0	0
		′		y
10)	xy		− y cosln x		= 0 .

7.5. Найти общие решения дифференциальных уравнений, удовлетво-

ряющие условиям:

1)

y′+ y = cos x ;

2)

y′− y = sin x ;

3)

xy′+ y −ex = 0 ;

4)

(1 + x2 ) y′− 2xy = (1 + x2 )2 ;

′

−x2

′

1

y

+ 2xy = xe ;

5)

6)

y

+ 2 y ctgx = sin x ;

y′

2 y

e−x2

xy′+ y − xy

2

ln x = 0 ;

7)

+ x −

x = 0 ;

8)

9)

y′cos x + y sin x =1;

10) (1 + x2 ) y′+ y = arctgx .

7.6. Найти общие или частные решения дифференциальных уравнений,

	удовлетворяющие условиям:
	1)	y′− ytgx + y2 cos x = 0,								y0 =1, x0 = 0 ;
	2)	y′+	y			+ y2		= 0, y0 =		1 , x0 = 0 ;
			x +1
										2
	3)	y′+ y2 = 2x−4 ;
	4) xy′− 4 y − x2							y = 0, y0 =1, x0 =1;
		y′+	2 y			2		y
	5)		x	−					= 0 .
							cos2 x

162

7.7. Найти общие или частные решения дифференциальных уравнений, удовлетворяющие условиям:

1)(x2 +1)y′+ 2xy2 = 0 , y(0) = −1;

2)y′ = 6x 3 y2 , y(1) =8 ;

3)(x +1)3 dy − 2(y − 2)2 dx = 0 , y(0) =3 ;

		π				2
	4) y dx −ctg x dy = 0 ,	y			=		;
			4			2

5)xy′− y = 0, y(−2) = 4 ;

6)xy′+ y = 0, y(−2) = 4 ;

7)yy′+ x = 0, y(−2) = 4 ;

8)y′ = y, y(−2) = 4 ;

9)(x2 +1)y′+ 4xy = 3 , y(0) =1;

10)x y′+ y = 3x2 , y(2)= 3 ;

11)xy′+ y = (x +1)ex , y(1)= e ;

12)y′+ 2xy = sin x e−x2 , y(0) = 2 ;

13)y′+ 2 y cos x = sin 2x e−2sin x , y(0) = 12 ;

14)y′− yctgx = 2xsin x, y(0) = 3 ;

15)xy′+ y = 1 +1x2 , y(1) = 0 ;

16)cos xy′− y = 3x2esin x , y(0) = 5 ;

17)(1 + x2 ) y′+ 2xy = e2 x , y(0) = −2 ;

18)(y + x2 + y2 )dx − xdy = 0 , y 1 = 0 ;

2

	19)	y	′	1 − y2		= 0 ;
				+ 1	− x2

20)xy′cos xy = y cos xy − x, y(1) = 0 ;

21)y 2 y′ =1 − 2x ;

22)xy′ = y(ln y −ln x), y(1)= e2 ;

23)y′+ 2xy = xe−x2 ;

24)(1 − x)t2 xt′ + x2 = −tx2 ;

25) 2(y′+ xy)=(1 + x)e−x y2 , y(0)= 2 .

163

ТЕМА 2

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА

В общем случае дифференциальные уравнения второго порядка имеют

вид

F(x, y, y′, y′′) = 0 .

Дифференциальное уравнение второго порядка, разрешенное относительно старшей производной, соответственно имеет вид

y	′′	′	(7.25)
		= f (x, y, y ) .

Общее решение дифференциального уравнения второго порядка содержит две произвольные постоянное C1 и C2 :

y =ϕ(x,C1,C2 ) .

При заданных начальных условиях
y(x0 ) = y0 , y′(x0 ) = y0′	(7.26)

постоянные C1 и C2 можно выбрать так, что функция y =ϕ(x,C1,C2 ) будет удовлетворять начальным условиям.

Дифференциальные уравнения второго порядка, допускающие понижение порядка

1) Уравнение вида
y′′ = f (x) ,	(7.27)

где f (x) – заданная непрерывная функция, решается последовательным интег-

рированием правой части.

2) Пусть дифференциальное уравнение (7.25) не содержит в явной форме искомой функции y , т.е. имеет вид

F(x, y′, y′′) = 0 .

Тогда, используя замену y′ = z y′′ = z′, получаем дифференциальное уравнение первого порядка

164

′	(7.27)
F(x, z, z ) = 0 .

Если найдено общее решение z = z(x,C) дифференциального уравнения(7.27),

томожетбытьнайденоиобщеерешениедифференциальногоуравнения(7.25):

y′ = z(x,C) y = ∫z(x,C)dx +C1 .

3)Уравнение вида

x= f ( y′′)

решается с помощью подстановки y′′ = z .

	4) Уравнение
			′	′′
			F( y, y , y ) = 0 ,
не содержащее в				явной		форме переменной x , подстановкой y′ = p ,
y′′ =	dp	dp
	dx	= p dy	приводится к виду
						= 0 .
			F y, p, p dp
				dy

Примеры решения задач

Пример 7.15. Найти общее решение дифференциального уравнения y′′ = x +sin x .

Решение. Последовательно интегрируем обе части уравнения:

∫y′′dx = ∫(x +sin x)dx y′ = x2 −cos x +C1

2

	∫	′	∫	x2
		y dx =
					2
						−cos x +C1 dx.

Из последнего равенства находим общее решение исходного дифференциального уравнения

165

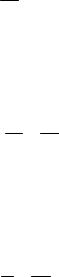
y = x3 −sin x +C1x +C2 , 6

где C1, C2 – произвольные постоянные.

Пример 7.16. Найти общее решение дифференциального уравнения y′′+ yx′ − x12 = 0 .

Решение. Заданное уравнение не содержит в явном виде переменной y , решение находим, используя подстановку y′ = z . Тогда y′′ = z′ и уравнение принимает вид:

z′+ xz − x12 = 0 .

Получено линейное дифференциальное уравнение первого порядка. Решаем его используя замену z = uv :

′

′

+

1

uv =

1

′

′

+

v

=

1

2

2 .

u v +uv

x

x

u v +u v

x

x

Отсюда

′		v		′	1
	+ x		= 0				(7.28)
v				и u v = x2 .

Решаем первое уравнение из (7.28):

	dv	= −	v	dv	= − dx	ln | v |= ln	1	v =	1 .
	dx		x				x
				v	x				x

Решаем второе уравнение из (7.28), полагая v = 1x :

u′

=

1

du

= 1 du = dx

u = ln | x | +C .

x

x2

dx

x

x

z =

ln | x |

C

y

′

ln | x |

C

Следовательно,

+ x

или

=

+ x . Дифференцируя обе

x

x

части последнего равенства, находим общее решение исходного уравнения:

∫

′

∫

ln | x |

C

ln2 | x |

y dx =

+

dx y =

+C ln | x | +C1 .

2

x

x

166

Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами

Дифференциальное уравнение называется линейным, если искомая переменная и ее производная входят в уравнение в первой степени, т.е.

y′′+ p(x) y′+ q(x) y = f (x) .

(7.29)

Если p(x) ≡ p и q(x) ≡ q – постоянные, то уравнение называется линей-

ным дифференциальным уравнением с постоянными коэффициентами.

Функция f (x) называется правой частью уравнения (7.29). Если f (x) ≠ 0 , то уравнение (7.29) называется линейным неоднородным уравнением

или уравнением с правой частью. Если f (x) ≡ 0 , то уравнение (7.29) называется

линейным однородным уравнением или уравнением без правой части.

Если y1 (x) и y2 (x) – два частных решение линейного однородного диф-

ференциального уравнения второго порядка
y′′+ py′+ qy = 0 ,	(7.30)

то y1(x) + y2 (x) – также является решением этого уравнения.

Если y1 (x) – решение уравнения (7.30) и C – произвольная постоянная, то Cy1(x) также есть решение уравнения (7.30).

Если y1 (x) и y2 (x) – два линейно независимых решения дифференциального уравнения (7.30), то

yo.o. = C1 y1(x) +C2 y2 (x) ,	(7.31)
где C1 и C2 – произвольные постоянные, есть общее решение	yo.o. уравнения
(7.30).

Таким образом, для того, чтобы найти общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами (7.30), достаточно найти два частных линейно независимых решения этого уравнения.

Частные решения ищут в виде y = ekx , где k – искомая постоянная. Для

определения постоянной k для однородного уравнения (7.30) составляют ха-

рактеристическое уравнение

k2 + pk + q = 0 .

(7.32)

Рассмотрим зависимость между решением характеристического уравнения и общим решением дифференциального уравнения (7.30).

1) Корни k1, k2 характеристического уравнения (7.32) действительны и

различны (дискриминант D квадратного уравнения (7.32) больше нуля, k1 ≠ k2 ). Тогда общее решение дифференциального уравнения (7.30) имеет вид:

167