Практикум по высшей математике_часть 2

6a +1,8782b =134,	a =18,8,
1,8782a +1,1921b = 53,3148	b =16,4.

Тогда искомая функциональная зависимость имеет вид:

			y =18,8 +16,4 .
				x
		Пример 5.26. Предполагая, что рост производительности труда y описы-
вается показательной кривой							y =bat			(см. табл. 5.8), оценить с помощью МНК
параметры a и b .
														Таблица 5.8. Исходные данные
				t				1			2			3	4	5		6	7
		производительность, y						12,1			13,5		18,0		22,2	22,3		23,6	24,8
		Решение. Рассчитываем вспомогательные величины (см. табл. 5.9).
													Таблица 5.9. Основные расчеты
		i		t				t2					y		z = ln y			t ln y =t z
	1			1			1					12,1			2,493205			2,493205
	2			2			4					13,5			2,60269			5,205379
	3			3			9					18			2,890372			8,671115
	4			4			16					22,2			3,100092			12,40037
	5			5			25					22,3			3,104587			15,52293
	6			6			36					23,6			3,161247			18,96748
	7			7			49					24,8			3,210844			22,47591
		Σ		28			140						–		20,56304			85,73639
		Составляем систему нормальных уравнений (5.20)
			140B + 28A =85,74,							B = 0,12,
			28B + 7 A = 20,56,							A = 2,44.
		Отсюда ln b = 0,12, следовательно, b = e0,12												=1,13. Аналогично, ln a = 2,44 ,
следовательно,				a = e2,44 =11,47 . Тогда, искомая функциональная зависимость:

y =11,47 1,13t .

Уравнение показывает, что средний рост производительности труда составляет 13% ежегодно.

Задания для самостоятельного решения

50

В задачах 5.90-5.96, используя метод наименьших квадратов, получить линейную зависимости по следующим данным:

5.90.					4
	X	1	2	3		5	6
	Y	5	7	10	9	13	15
	5.91.				19
	X	16	17	18		20	21
	Y	28	15	6	1	0	3
	5.92.				1,2
	X	0,6	0,8	1		1,4	1,6
	Y	3,2	1,8	1,1	0,3	-0,2	-2,2
	5.93.				17
	X	12	14	15		19	23
	Y	-10	-15	-19	-21	-23	-25
	5.94.				8
	X	-1	4	7		10	12
	Y	-2	-7	-12	-25	-88	-150
	5.95.				1
	X	0,5	0,8	0,95		1,5	2
	Y	-2	-1,8	-1,5	-1,1	-0,8	-0,5
	5.96.
	X	11	15	20	25	27	30
	Y	25	10	5	-4	-10	-20

5.97. Средняя годовая численность рабочих на некотором предприятии характеризуется следующими условными данными:

Годы	1	2	3	4	5	6	7
Численность рабочих	1100	1453	1899	2295	2483	2558	2747

Предполагая, что рост численности рабочих и служащих происходил по показательной кривой y =bax , найти параметры a и b этой зависимости, пользуясь методом наименьших квадратов.

5.98. Результаты наблюдений за среднемесячным объемом продаж представлены в следующей таблице:

t	объем продаж, y	t	объем продаж, y
1	26559	7	21054
2	20986	8	24873
3	27645	9	38356
4	16947	10	65691
5	14150	11	81770
6	22705	12	93538

51

Установить вид функциональной зависимости и, используя метод наименьших квадратов, найти параметры этой зависимости.

5.99. Данные о выпуске продукции y (млн. грн.) на некотором предпри-

ятии представлены в следующей таблице:
								5
	Годы	1	2	3		4			6	7	8
	y	9,5	9,7	10,1		10,5		10,4	11,4	11,8	12,0
	Найти уравнение, характеризующее объем выпускаемой продукции.
	5.100.Зависимость между себестоимостью							y (грн.) одного экземпляра

книги и ее тиража x (тыс. экз.) представлены в таблице:

x	1	2	3	5	10	20	30	50	100	200
y	10,15	5,25	4,08	2,85	2,11	1,62	1,41	1,30	1,21	1,15

Определить вид зависимости между себестоимостью книги и ее тиражом. Используя метод наименьших квадратов, найти параметры установленной зависимости.

Понятие задачи математического программирования

Задача математического программирования (планирования) заключается в вычисление экстремального (максимального или минимального) значения функции f (x1, x2 ,..., xk ) многих переменных при наличии ограничений

g(x1, x2 ,..., xk ) ≤ 0 , представленных в виде неравенств.

Определенная таким образом задача называется задачей оптимизации и имеет следующий вид.

Найти max(min) функции f (x1, x2 ,..., xk ) :

f (x1, x2 ,..., xk ) → max(min)	(5.13)
при условиях
g1(x1, x2 ,..., xk ) ≥ 0,
g2 (x1, x2 ,..., xk ) ≥ 0,	(5.14)
gm (x1, x2 ,..., xk ) ≥ 0,
x1 ≥ 0, x2 ≥ 0,..., xk ≥ 0 .	(5.15)
Функцию f (x1, x2 ,..., xk ) называют целевой функцией,	неравенства вида

(5.14) – специальными ограничениями (балансовыми условиями), неравенства (5.15) – общими ограничениями (граничными условиями) задачи математическо-

го программирования (ЗМП).

Точка (x1, x2 ,..., xk ) , удовлетворяющая общим и специальным ограничени-

ям, называется допустимым решением ЗМП.

52

Множество всех допустимых решений ЗМП называется допустимым множеством этой задачи.

Точка (x10 , x20 ,..., xk0 ) называется оптимальным решением ЗМП, если она является допустимым решением и на этой точке целевая функция f (x1, x2 ,..., xk )

достигает глобального максимума (глобального минимума).

В экономической теории ЗМП часто сводится к задаче на условный экстремум. Кроме того, на практике часто встречаются задачи, в которых функции f (x1, x2 ,..., xk ) и gi (x1, x2 ,..., xk ), i =1,2,..., m являются линейными. Тогда говорят

озадаче линейного программирования.

Вкачестве примера рассмотрим задачу о распределении ресурсов (задача

опроизводственной программе). Предприятие имеет в своем распоряжении определенное количество ресурсов R1, R2 ,..., Rm : рабочую силу, деньги, сырье,

оборудование, производственные ресурсы, площади и т.д. Указанные ресурсы ограничены соответственно величинами b1,b2 ,...,bm . Предприятие выпускает k

видов товаров T1,T2 ,...,Tk . Пусть aij – число единиц ресурса Ri , i =1,2,..., m , необходимое для производства единицы товара Tj , j =1,2,...,k . Доход, получае-

мый предприятием от единицы каждого вида товаров, соответственно равен c1,c2 ,...,ck . Пусть xi – объем выпуска продукции i -го вида. Тогда эта задача

формализуется следующим образом:

c1x1 + c2 x2 +... + ck xk → max ,

a11x1 + a12 x2 +... + a1k xk ≤ b1, a21x1 + a22 x2 +... + a2k xk ≤ b2 ,

am x1 + am2 x2 +... + amk xk ≤ bm , x1 ≥ 0, x2 ≥ 0,..., xk ≥ 0.

Графический метод решения задач линейного программирования

В случае двух переменных задачу линейного программирования можно решить графическим методом.

Пусть целевая функция двух переменных имеет вид

z(x1, x2 ) = c1x1 + c2 x2 ,

(5.16)

балансовые условия:

53

a11x1 + a12 x2 ≤ b1,
a21x1 + a22 x2	≤ b2	,	(5.17)

am x1 + am2 x2 ≤ bm ,

где aij > 0, (i =1,m, j =1,2) и c1, c2 > 0 , а граничные условия

x1 ≥ 0, x2 ≥ 0.

(5.18)

Необходимо найти такие значения переменных x1 и x2 , чтобы выполня-

лись условия (5.17) – (5.18) и целевая функция (5.16) принимала наибольшее (наименьшее) значение.

При решении задачи линейного программирования графическим методом используется понятие линии уровня. При этом не сложно показать, что в случае линейной функции z(x1, x2 ) = c1x1 + c2 x2 все линии уровня являются прямыми,

перпендикулярными общему вектору нормали c = (c1,c2 ) = grad z .

Алгоритм графического метода

1)Построить множество всех допустимых значений, удовлетворяющих условиям (5.17).

2)Если множество допустимых значений пустое ( X = ), то задача не имеет решения.

3)Если множество допустимых значений не пустое ( X ≠ ), то необхо-

димо построить прямые уровня z(x1, x2 ) =α при монотонном изменение α от −∞ до +∞. При увеличение α прямая z(x1, x2 ) =α смещается параллельно в

направлении вектора c .

4) Если A – первая точка встречи прямой уровня с областью X , то min z = z( A) . Если A – последняя точка пересечения линии уровня с областью

X , то max z = z( A) . Если не существует первой точки пересечения линии уровня и области X , то min z = −∞, и задача на минимум не имеет решения. Если не существует последней точки пересечения, то max z = +∞, и задача на макси-

мум не имеет решения.

5) Если целевая функция достигает своего наибольшего (наименьшего) значениявдвухугловыхточках A и B , торешениемзадачиявляетсяотрезок AB и

zopt = z(A)= z(B),

x1 =αx1A +(1−α)x1B , x2 =αx2A +(1−α)x2B , 0 ≤α ≤1.

Примеры решения задач

54

Пример 5.27. Найти значения x1 и x2 ( x1 ≥ 0, x2 ≥ 0 ), для которых целевая функция z = x1 + 2x2 принимает наибольшее и наименьшее значения при ограничениях

−2x1 −3x2 ≤ −6,	(1)
−x1 + x2 ≤ 2,	(2)
2x1 + x2 ≤ 5.	(3)

Решение. Строим область допустимых решений. Для этого на числовой плоскости строим прямые 2x1 +3x2 = 6 , −x1 + x2 = 2 , 2x1 + x2 = 5 . Затем определяем множество точек, удовлетворяющих ограничениям. Область допустимых решений – заштрихованный треугольник на рис. 5.11. Строим вектор c и линии уровня, проходящие перпендикулярно вектору c . Перемещая линию уровня в направление вектора c , находим последнюю точку (точка A ) пересечения прямой уровня и допустимого множества X . Аналогично перемещая линию уровня в направление, противоположном вектору c , находим первую точку (точка B ) пересечения прямой уровня и допустимого множества X (рис. 5.11).

x2
6
5		(3)			(2)
4			A
3
2	B
1		c	C	(1)
0								x1
		1	2	3	4	5
0							6
-1
-2

Рис. 5.11. Область допустимых решений

Таким образом, точка A является точкой максимума, точка B – точка минимума.

Определяем координаты точек A и B .

Чтобы найти координаты точки A – точки пересечения прямых (2) и (3), надо найти решение системы уравнений

−x + x = 2,		x =1,
	1 2	1
2x1 + x2 = 5,		x2 = 3.

Тогда A = A(1;3) и zmax = z(A)=1+ 2 3 = 7 .

Аналогично находим координаты точки B , как точки пересечения пря-

мых (1) и (2)

55

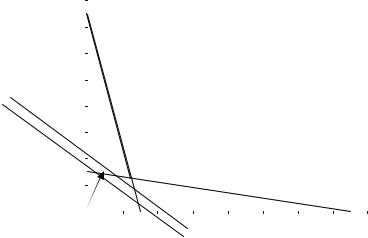
2x +3x = 6,			x = 0,
	1	2	1
−x1 + x2 = 2,			x2 = 2.

Тогда B = B(0;2) и zmin = z(B)= 0 + 2 2 = 4 .

Пример 5.28. В рацион питания больного включены два продукта питания A и B , содержащие белки и углеводы. Весовая единица продукта A содержит 5 единиц белка и 1 единицу углевода, весовая единица продукта одну и пять единиц соответственно. Больной ежедневно должен получать минимум 15 единиц белка и 15 единиц углевода. При каком рационе затраты будут минимальными, если цена продукта A составляет одну денежную единицу, а цена продукта B – 3 денежные единицы?

Решение. Предположим, что в ежедневный рацион питания больного включены x1 весовых единиц продукта A и x2 весовые единицы продукта B .

Тогда ежедневные затраты составят z = x2 +3x2 денежные единицы. При этом переменные x1 и x2 должны удовлетворять условиям

x1 +5x2 ≥15, 5x1 + x2 ≥15, x1 ≥ 0, x2 ≥ 0.

Строим область допустимых значений, вектор c и линии уровня (рис. 5.12).

x	16			(2)
	2
	14
	12
	10
	8
	6				A
	4
	2			c							(1)
	0											x1
				2	4	6	8	10	12	14
	0										16

Рис. 5.12. Область допустимых решений

Целевая функция z = x2 +3x2 принимает минимальное значение в точке A(2,5;2,5) . Таким образом, в ежедневный рацион больного необходимо вклю-

чить по 2,5 весовых единиц продуктов A и B . При этом затраты составят zmin = 2,5 +3 2,5 =10 денежных единиц.

Заметим, что в рассматриваемом примере задача на максимум целевой функции не имеет решения.

56

Задания для самостоятельного решения

5.101. Решить задачу линейного программирования, используя графический метод:

1) Z = x1 + x2 → max				2) Z = −2x1 − x2 → min
x + 2x			≤10,	x + 2x	≤8,
	1	2		1	2
2x1 + x2 ≤8.				x1 +3x2 ≥ 9,
x	≥ 0; x		≥ 0;	6x1 +5x2 ≥ 30, x1, x2 ≥ 0
1	2

5.102. Для изготовления нового лекарства фармацевтическая фирма используетдваингредиента A1 и A2 . Вкаждойупаковкеэтоголекарствадолжнобыть не менее 40 мг. витамина C и 30 мг. витамина B . Известно, что ингредиент A1 содержит 5 мг. витамина B , ингредиент A2 – 3 мг. Кроме того, известно, что ингредиенты содержат по 5 мг. витамина C . Определить количество ингредиентов A1 и A2 , при котором затраты производства будут минимальными, если порция каждого ингредиентастоит0,1 экюи1,15 экюсоответственно.

5.103. Фабрика производит два вида красок: первый – для наружных, а второй – для внутренних работ. Для производства красок используются ингредиенты A и B . Максимальные суточные запасы этих ингредиентов составляют 6 и 8 т. соответственно. Известнырасходы A и B на1 тсоответствующихкрасок

Ингредиенты	Расход ингредиентов		Запас,
	Краска 1 – го вида	Краска 2 – го вида	т./сутки
A	1	2	6
B	2	1	8

Изучение рынка сбыта показало, что суточный спрос на краску 2-го вида никогда не превышает спроса на краску 1-го вида более чем на 1 т. Кроме того, установлено, что спрос на краску 2-го вида никогда не превышает 2 т. в сутки. Оптовые цены одной тонны красок равны: 3 тыс. грн. для краски 1-го вида; 2 тыс. грн. для краски 2-го вида. Составить план производства красок, при котором будет достигнута максимальная прибыль.

5.104. Суточный рацион человека должен содержать не менее 120 условных единиц (усл. ед.) белков, не менее 70 усл. ед. жиров и не менее 10 усл. ед. витаминов. Содержание их в каждой единице продуктов A и B равно соответственно (0,2; 0,075; 0) и (0,1; 0,1; 0,1) усл. ед. Стоимость 1 ед. продукта A – 2 у.е., B – 3 у.е. Определить минимальную стоимость набора из продуктов A и B , обеспечивающего необходимое количество питательных веществ.

5.105. Заказ по производству 32 изделий вида A и 4 изделий вида B выполняют две бригады. Производительность первой бригады по производству изделий A и B составляетсоответственно4 и2 изделиявчас, фондрабочеговремениэтойбригады 9,5 ч. Производительность второй бригады – соответственно 1 и 3 изделия в час, а ее фонд рабочего времени – 4 ч. Затраты, связанные с производством единицы изделия, дляпервойбригадыравнысоответственно9 и20 грн., длявторойбригады– 15 и 30 грн. Найти оптимальный объем выпуска изделий, обеспечивающий минимальныезатратынавыполнениезаказа.

57

Задания для индивидуальной работы № 11

Задание 11.1. Найти полный дифференциал для функций z = f (x, y) (см.

табл. 11.1).

														Таблица 11.1
Номер		z = f (x, y)								Номер			z = f (x, y)
варианта										варианта
1		z = sin (y2 x + xy)								16	z = ctg (			x3 + 2 y2 )
2		z = ex2 y−y2								17	z =(3xy3 − 2x)17
3		z = 2xy−x2								18	z = tg (x2 y −3xy3 )
4		z = −3cos(x2 y3 − 2xy)								19	z = 4 2x2 y − y3
													Окончание табл. 11.1
5		z = tg (2xy − x2 )								20	z = ctg (xy3 −9x)
6			3			3		1		21	z =			4
								3							2
		z =(5y − 2x y)											(2x3 −3xy)
7		z = ctg (x2 y3 −7xy)								22	z = ln (x2 y3 + x )
8		z = −		1						23	z =		−1
					− x3								7 x3 y	−3y2
		3 5xy
9		z = 5 2 y2 −3xy								24	z = 3sin (x2 +3xy3 )
10		z = 7 cos(x4 −3xy3 )								25	z =10xy3 −y2
11		z = ln (x2 − y3 )								26	z = 2sin (y − x2 y)
12		z = cos(x3 y +5xy2 )								27	z = 7x2 y−y3
13		z = 3 2xy2 − x5								28	z = tg ( x2 y + 2x2 )
14		z = ln (x4 − 2xy + xy2 )								29	z =(7 y3 −2x4 y)17
15		z = 52 x−x2 y−3 y								30	z = e2 x2 y−3x
Задание 11.2. Для функции z = f (x, y) найти частные производные второ-
го порядка (табл. 11.2).
														Таблица 11.2
Номер		z = f (x, y)								Номер			z = f (x, y)
варианта										варианта
58

1		z = x2 y −2xy +3xy3	16			z = x3 −2xy2 +3xy3
2		z = 2x3 y −3xy2 +3y3	17			z = 4xy −2xy2 +5y3
3		z = x2 y + 2xy +3y −2x	18			z = x4 + 2x2 y +3y3 −2xy
4		z = x5 y −3xy2 +3y	19			z = x3 y + 2xy +3y2 +5
5		z = x3 + 2x2 y +5y −7x	20			z = x3 + 2xy2 +3y2 −15
6		z = x3 y +6xy2 +8y −12	21			z = xy2 −3xy +17 y −5x
7		z = x7 + 2x2 y −5y −2x2	22			z = xy −4xy2 −5y2 +3x
8		z = x −3x2 y +5y2 + 2y	23			z = x3 y −7xy2 −17 y +3x
9		z = x4 +9x2 y −17 y +19	24			z = xy3 −5x2 y +7x −4
10		z = xy2 −3x2 y +7x −5	25			z =3x5 −2x2 y +3y3 +17
11		z = xy2 −5xy +3y3 + 23	26			z = 7x5 y −6xy2 +3y3 −17
12		z =3x7 + 2x4 y +3y2 −19	27			z = −3x2 + 2xy2 −7 y3 +12
						Окончание табл. 11.2
13		z = 2x3 y −8xy2 +11y −2	28			z =5x3 −7xy2 +3х−5у
14		z =17xy2 −5xy +3х+7 у	29			z =15x2 −7xy +12x
15		z =3x4 y + 2xy +3y +17	30			z = x7 −2x2 y +3хy3 +8у−1
Задание 11.3. Найти частные производные первого порядка ∂z и							∂z
(табл. 11.3).						∂x	∂y
						Таблица 11.3
Номер		f (x, y, z)= 0		Номер		f (x, y, z)= 0
варианта				варианта
1		x2 y +3y2 +5z3 −6xz = 0		16		5x2 +7xy2 + z2 + yz = 0
2		2x2 y + 4y2 +5z3 −5xz = 0		17		5x2 +6xy2 + z2 + 2 yz = 0
3		3x2 y +5y2 +5z3 −4xz = 0		18		5x2 +5xy2 + z2 +3yz = 0
4		4x2 y +6y2 +5z3 −3xz = 0		19		5x2 + 4xy2 + z2 + 4yz = 0
5		5x2 y +7 y2 +5z3 −2xz = 0		20		5x2 +3xy2 + z2 +5yz = 0
6		3xy2 +6y2 +7z2 + xy = 0		21		5x2 +7x2 y2 + z2 + xz = 0
7		3xy2 +5y2 +7z2 + 2xy = 0		22		4x2 +7x2 y2 + z2 + 2xz = 0
8		3xy2 + 4y2 +7z2 +3xy = 0		23		3x2 +7x2 y2 + z2 +3xz = 0
9		3xy2 +3y2 +7z2 + 4xy = 0		24		2x2 +7x2 y2 + z2 + 4xz = 0
10		3xy2 + 2y2 +7z2 +5xy = 0		25		x2 +7x2 y2 + z2 +5xz = 0
11		2x2 +3y2 +5z2 +5xy = 0		26		2x2 y −5y3 + z2 +6xy = 0

59