Практикум по высшей математике_часть 2

z′x	=350 −4x − 2 y = 0,	2x + y =175,	x = 60,
	= 450 −6 y − 2x = 0,
z′y		x +3y = 225	y =55.

Проверяем достаточное условие экстремума:

′′	,	′′	′′
A = zxx = −4		B = zxy = −2,	C = zyy = −6 ,

D = AC − B2 = 24 − 4 = 20 > 0 .

Так как D >0 и A < 0 , то в точке (60, 55) функция прибыли фирмы имеет

максимум.

Оптимальный объем выпуска продукции x + y =115 , максимальная прибыль фирмы

zmax = z(60,55) =

= −2 (60)2 − 2 60 55 −3 (55)2 +350 60 + 450 55 −10 = 22865 .

При этом на первом рынке реализуется 60 усл. ед. продукции (или 52% от общего объема производства), на втором рынке реализуется 55 усл. ед. продукции (или 48% от общего объема производства).

Задания для самостоятельного решения

5.63. Найти экстремум функции:

1)	z = 2x3 + xy +0,5y2 + y ;	2)		z = x3 +3xy +3y2 +9y ;
3)	z = x3 + 2xy + 2y2 + 4y ;	4)	z = 2x2 +3y2 −2xy −16x −8y ;
5)	z = 4(x − y) − x2 − y2 ;	6)	z = x2 + xy + y2 + x − y +1;
7)	z = −x2 − y2 + xy + 20x +15y ;	8)	z = −2x2 − y2 + 20x +10 y ;
9)	z = x2 + 2x + y + y2 ;	10)		z = x2 −12x + y2 −27 y ;
11)	z = x2 +( y −1)2 ;	12)		z = −10x2 − 1 y2 + xy +18x ;
	z = x3 + y3 −3xy ;			4
13)		14)		z = y x − y2 − x +6 y ;
15)	z = x4 + y4 −2x2 + 4xy −2y2 ;	16)		z = −x2 −3y2 − xy + 28x +80 y ;
17)	z = 2x3 + y3 −6x −12y +5;	18)		z = x2 y2 + x2 + y2 ;
					x
19)	z =1 − x2 + y2 ;	20)		z = e		(x + y2 ) .
					2

5.64. Найти наименьшее и наибольшее значение функции z = x2 − y2 в круге x2 + y2 ≤ 4 .

40

5.65.Найти наименьшее и наибольшее значение функции z = xy в круге

x2 + y2 ≤9.

5.66.Найти наименьшее и наибольшее значение функции z = xy + x + y в квадрате, ограниченном прямыми x = 0, x = 2, y =1, y =3 .

5.67. Найти	наименьшее	и	наибольшее	значение	функции
z = x2 +3y2 + x − y	в треугольнике,		ограниченном	прямыми	x =1,	y =1,
x + y =1.
5.68. Найти	наименьшее и наибольшее значение функции
z = x2 y(4 − x − y) в	треугольнике,	ограниченном		прямыми x =0,		y = 0 ,
x + y = 6 .
5.69. Найти	наименьшее	и	наибольшее	значение	функции
z = x2 − xy + y2 −4x	в замкнутой области, ограниченной прямыми x =0,					y = 0 ,
2x +3y =12 .

5.70.Найти экстремум функции f (x, y) = x2 + y2 , если x + y = 2 .

5.71.Найти экстремум функции f (x, y) = 2x2 + y2 −6x +16 , если x + y = 3 .

5.72.Найти экстремум функции f (x, y) =3y2 −4x2 +66x −70y +100 , если

x+ y = 20 .

5.73.Найти экстремум функции f (x, y) = x3 + y3 , если x + y = 2 .

5.74. Найти

экстремум

функции f (x, y) = −x2 −3y2 +6x + 4y + 4 ,

если

x + y =1.

5.75. Найти

экстремум

функции

f (x, y) = x2 + y2 − xy + x + y ,

если

x + y = −3 .

5.76. Используя

метод

Лагранжа,

найти

экстремум

функции

f (x, y) = −x2 −2y2 + 2xy +100, если x + 2 y =10 .

5.77. Используя

метод

Лагранжа,

найти

экстремум

функции

f (x, y) =3x2 + 4y2 + 2xy +6 , если x + y = 5 .

5.78. Используя

метод

Лагранжа,

найти

экстремум

функции

f (x, y) =

1

+

1

, если x + y = 2 .

x2

y2

5.79. Используя

метод

Лагранжа,

найти

экстремум

функции

f (x, y) = −x2 − y2 +16x +14 y , если x + y = 5 .

5.80. Используя

метод

Лагранжа,

найти

экстремум

функции

f (x, y) = 1 +

1

, если

1

+

1

=

1 .

x2

x

y

y2

4

5.81. Используя

метод

Лагранжа,

найти

экстремум

функции

f (x, y) = −x2 −2 y2 +10x + 20y , если x + y =115 .

41

5.82. Используя метод Лагранжа, найти экстремум функции

f(x, y) = 2x + y , если x2 + y2 =1.

5.83.Используя метод Лагранжа, найти экстремум функции f (x, y) = xy

при условии, что x2 + y2 = 2 .

5.84. На расширение производства было решено выделить 200 000 грн. Известно, что если на новое оборудование затратить x тыс. грн., а на заработную плату новых работников – y тыс. грн., то прирост объема производства

составит Q = 0,001x0,6 y0,4 . Как распределить выделенные денежные средства

так, чтобы прирост был максимальным?

5.85. На предприятие используется два типа технологического оборудования A и B . Выпуск единицы продукции требует 24 часа работы оборудования A и B в любой их комбинации. Прибыль от единицы продукции задается функцией вида

PR = 70x + 22 y −2x2 − y2 ,

где x – время работы оборудования A (в часах), y – время работы оборудова-

ния B .

Найти оптимальное время работы оборудования каждого типа, позволяющее получить максимальную прибыль. Определить максимальную прибыль от единицы продукции.

5.86. Функция полных издержек двухпродуктовой фирмы задана уравнением C = x2 + 4y2 +100 , где x и y – объемы выпуска товаров первого и второго вида соответственно. Цены на эти товары равны p1 = 40 и p2 = 64 . Опреде-

лить, при каких издержках достигается максимум прибыли.

5.87. Зависимость урожайности подсолнечника от затрат x (грн/га) на удобрения и затрат y (грн.) на семена имеет вид z = 3 x + 2 y . Прибыль от реализации продукции выражается функцией p = C1 y − x − y −C2 , где C1 – выручка от реализации 1 ц. подсолнечника и C2 – постоянные затраты, не зависящие от x и y . Найти значения затрат на удобрения и затрат на семена (на один

гектар) при которых прибыль была бы максимальной.

5.88. На производстве работают две группы рабочих: механики и электрики. Продуктивность P (в час) всех рабочих может быть выражена функцией

P = −3x2 −4y2 +90x +80y , где x – общее число механиков, y – электриков.

Известно, что механик получает 2 у.е. в час, электрик – 3 у.е. в час. Определить наибольшую продуктивность, а также необходимое для этого число рабочих, если общая зарплата (за час работы) равна 60 у.е.

5.89. Для изготовления нового лекарства фармацевтическая фирма использует два ингредиента x и y . Функция затрат на производство одной упа-

ковки лекарств имеет вид: C = 2x2 + y2 + 2xy −16x −2y . В каждой упаковке этого лекарства должно быть 20 граммов витамина B . Известно, что ингредиент x

42

содержит 3г. витамина B , ингредиент y – 5г. Определить количество ингредиентов x и y , при котором затраты производства будут минимальными.

Метод наименьших квадратов

Часто при решении практических задач возникает необходимость установить аналитическую зависимость между двумя величинами, значения которых получены экспериментально. Пусть в результате исследования некоторого экономического процесса (например, дохода производства) получены n значений

x1, x2 ,..., xn независимой переменной x					и n значений y1, y2 ,..., yn зависимой пе-
ременной (функции) y (табл. 5.1).
					Таблица 5.1. Экспериментальные данные
	xi	х1		x2		x3	…	xn
	yi	y1		y2		y3	…	yn

По табличным данным необходимо получить функциональную зависимость между переменными x и y , т.е. найти такую функцию, которая «наи-

лучшим» образом описывает зависимость переменной y от x . Табличные дан-

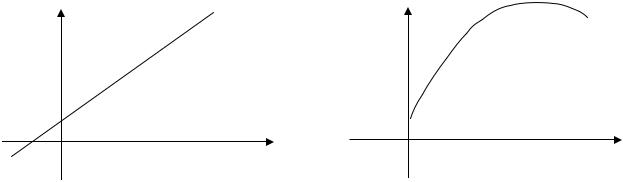
ные можно изобразить в виде точек на плоскости (рис. 5.8). Через полученное «облако» (или «поле») точек наблюдений нужно провести линию, которая среди всех линий будет «ближайшей» к точкам наблюдений. В качестве критерия близости используется минимум суммы квадратов разностей наблюдений зависимой переменной yi и теоретических, рассчитанных по уравнению регрессии

значений yˆi :

S= ∑ei2 = ∑( yi − yˆi )2 → min .

i=1 i=1n n

Поэтому и метод назвали методом наименьших квадратов (МНК).

у			•	у	• •	•	•	•• • •
		•	• •				•	•
	•				• •
		•	•	•
	• •	•	•		•
•	•			•
				••
• • •	•
•			х					х
а) взаимосвязь близка к линейной				б) взаимосвязь описывается
				нелинейной функцией

Рис. 5.8. «Поле» точек наблюдений

43

Вид функции устанавливается или из теоретических соображений или на основании характера расположения на координатной плоскости точек, соответствующих наблюдаемым значениям.

Определение уравнения прямой по эмпирическим данным называется вырав-

ниваниемпопрямой, уравненияпараболы– выравниваниемпопараболеит.д.

Наиболее часто встречаемые функциональные зависимости:

-линейная – y = ax +b ;

-квадратичная – y = ax2 +bx +c ;

-степенная – y = axb ;

-показательная – y = abx ;

-гиперболическая – y = a + bx .

Предположим,

что зависимость между переменными x

и y линейная:

yˆ = ax +b . Тогда

yˆi = axi +b ,

i =1,2,...,n .

Сумму

квадратов

погрешностей

n

n

∑ei2 = ∑( yi − yˆi )2

можно рассматривать как функцию двух переменных S(a,b)

i=1

i=1

n

n

− ˆ

n

2

S(a,b)

=

2

=

∑( yi

2

=

−

(axi

+

.

(5.13)

∑ei

yi )

∑ yi

b)

i=1

i=1

i=1

Таким образом, задача сводится к определению параметров a и b , при которых функция S(a,b) принимает минимальное значение, т.е. к вычислению

экстремума функции двух переменных.

Находим частные производные первого порядка функции S(a,b) и приравниваем их к нулю. Получаем систему уравнений относительно a и b

∂S		= −2	n
			y −(ax +b) x = 0,
	∂a		∑	i	i	i
			i=1
			n
∂S		= −2			−(ax	+b) = 0,
			y
	∂b		∑	i	i
			i=1

или после преобразований

	n	n	n
a∑xi2 +b∑xi = ∑xi yi ,
	i=1	i=1	i=1	(5.14)
	n	n
a∑xi +bn = ∑yi .
	i=1	i=1

44

Система (5.14) называется системой нормальных уравнений. Можно по-

казать, что эта система имеет единственное решение (a′,b′) и в точке (a′,b′) функция S(a,b) имеет минимум.

Предположим, что зависимость между переменными y и x может быть «наилучшим» образом описана с помощью функции y = ax2 +bx +c . Тогда функция S(a,b) имеет вид

n	n	n
S(a,b) = ∑ei2 = ∑( yi − yˆi )2 = ∑ yi −(axi2 +bxi + c)			2 .	(5.15)
i=1	i=1	i=1

Необходимые условия существования экстремума функции S(a,b) , определяемой равенством (5.15), представляют собой систему уравнений

	∂S		n	2	2
			= −2∑
		∂a		yi −(axi	+bxi + c) xi = 0,
			i=1
			n
	∂S			2	+bxi + c) xi = 0,
			= −2∑
		∂b		yi −(axi
			i=1
		∂S	n	2	+bxi + c) = 0.
		∂c	= −2∑= yi −(axi
			i 1

После преобразований последней системы, получаем систему уравнений для оценки параметров квадратичной зависимости:

	n	n	n	n
a∑xi4 +b∑xi3 + с∑xi2 = ∑x2i yi ,
i=1		i=1	i=1	i=1
	n	n	n	n
a∑xi3 +b∑xi2 + с∑xi				= ∑xi yi , .	(5.16)
i=1		i=1	i=1	i=1
	n	n		n
a∑xi2 +b∑xi + nс = ∑yi .
	i=1	i=1	i=1

Рассуждая аналогично, можно получить систему уравнений, позволяющую найти уравнение гиперболы y = a + b x , которая «наилучшим» образом отражает зависимость между переменными y и x , а именно

n

1

n

na +b∑

= ∑yi ,

1

i=1

xi

i=1

y .

(5.17)

n

n

1

n

a∑

+b∑

= ∑

i

.

x

x

2

i=1

i=1

i=1

x

i

i

i

45

Выравнивание с помощью показательной кривой

			Пусть x1, x2 ,..., xn – последовательность значений независимой перемен-
ной	x , а y1, y2 ,..., yn			– последовательность соответствующих значений зависи-
мой переменной y ,				т.е. задана последовательность точек	(x1, y1 ) , (x2 , y2 ) ,…,
(x , y		n	) . Необходимо найти показательную кривую y = abx ,		которая наилучшим
n
образом описывает зависимость между переменными y и x .
			Прологарифмировав обе части равенства y = abx , получаем
			ln y = ln a + xln b .		(5.18)
			Обозначим ln y = z , ln a = A , lnb = B . Тогда (5.18) принимает вид
			z = A + Bx .		(5.19)

Используя (5.14) составляем систему нормальных уравнений для оценки параметров A и B

B∑xi2		+ A∑xi	= ∑xi zi ,
	n	n	n
	i=1	i=1	i=1
	n	n
B∑xi + An = ∑zi ,
	i=1	i=1

где zi =ln yi .

Решение системы уравнений (5.20) позволяет найти значения гда a = eA , b = eB .

(5.20)

A и B . То-

Заметим, что в уравнение (5.18) можно использовать логарифм по произвольному основанию α .

Примеры решения задач

Пример 5.24. В табл. 5.2 представлен доход предприятия за пять лет. Найти с помощью МНК функцию, «наилучшим» образом описывающую зависимость дохода предприятия от времени.

Таблица 5.2. Данные примера 5.24

	Год, t	1						2		3		4		5
	Доход, у	24						27		30		37		42
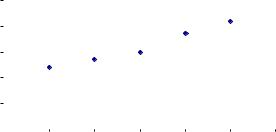
Решение: 1. Пары точек						(ti , yi ), i =1,2,...,5				наносим			на координатную
плоскость (рис. 5.9).
		50
		40
		30
		20
46		10
		0
		0			1	2		3	4	5		6

Рис. 5.9. «Поле» точек наблюдений для примера 5.24 Предположим, что зависимость между переменными y и t линейная, т.е.

y = at +b . Составляем систему нормальных уравнений (5.14). Расчеты прово-

дим с помощью таблицы (см. табл. 5.3)

Таблица 5.3. Расчет линейной модели

i		t			y			ty			t2
1	1			24			24			1
2	2			27			54			4
3	3			30			90			9
4	4			37			148			16
5	5			42			210			25
Σ		15			160			526			55

Тогда система нормальных уравнений принимает вид

55a +15b = 526,		55a +15(32 −3а) = 526,		a = 4,6,
	=160,		−3а,
15a +5b		b = 32		b =18,2.

Следовательно, уравнение искомой прямой: уˆ1 = 4,6t +18,2 . Предположим теперь, что зависимость между переменными y и t может

быть описана с помощью функции y = at2 +bt +c . Расчет также проводим, используя таблицу (см. табл. 5.4).

			Таблица 5.4. Расчет квадратической модели
i	t	y	ty	t2	t3	t4	t2 y
1	1	24	24	1	1	1	24
2	2	27	54	4	8	16	108
3	3	30	90	9	27	81	270
4	4	37	148	16	64	256	592
5	5	42	210	25	125	625	1050
Σ
	15	160	526	55	225	979	2044

Составляем систему нормальных уравнений (5.16).

979а+ 225b +55c = 2044,225a +55b +15c =526,55a +15b +5c =160.

Решаем систему методом Крамера.

47

∆ =	979							225	55		= 5 5							979					225					55		= 700,
	225							55	15									45					11					3
	55							15		5								11					3					1
∆1 =			2044					225		55					=5 5 2										1022			45	11					= 400,
			526					55		15															263			11	3
			160					15		5															80			3	1
∆2 =							979	2044		55					= 2 5					979						1022			11			=820,
							225	526		15										225						263			3
							55	160		5										55							80		1
∆3 =						979		225		2044							=5 2					979					45		1022							=15540 .
						225		55		526												225					11		263
						55		15		160													55					3	80

Отсюда

x	=	∆1	=	400 ≈	0,5714 ,	x	=	∆2	=	820	≈1,1714 ,
1		∆		700		2		∆		700
x	=	∆3	=	15540	≈ 22,2 .
3		∆		700

Следовательно, наилучшим образом подобранная парабола имеет вид

yˆ2 = 0,5714t2 + 1,1714t + 22,2.

Определим, какая из полученных линий лучше соответствует исследуемой зависимости. Для этого рассчитаем ошибки по каждой модели (см.

табл.5.5).

Таблица 5.5. Сравнение результатов

i	x	yˆ1	(yˆ − у)2	yˆ2		( yˆ	− у)2
			1		2
1	1	22,8	1,44	23,9428	0,003272
2	2	27,4	0,16	26,8284	0,029447
3	3	32	4	30,8568	0,734106
4	4	36,6	0,16	36,028	0,944784
5	5	41,2	0,64	42,342	0,116964
Σ	–	–	6,4	–		1,828573

48

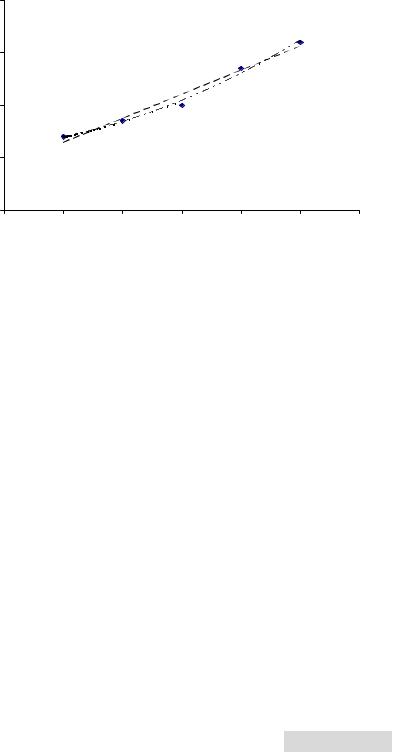
Так как сумма квадратов отклонений (yˆ2 − у)2 для параболы (1,828573) меньше, чем сумма квадратов отклонений (yˆ1 − у)2 прямой линии (6,4), то парабола лучшеотображаетзависимостьмеждупеременными x и y (см. рис. 5.10).

50

40

30

20

10

0

1

2

3

4

5

6

Рис. 5.10. Выравнивание по прямой линии и по параболе

Пример 5.25. Стаж рабочего x (в годах) и время на выполнение некоторой работы y (мин) представлены в табл. 5.6.

Таблица 5.6. Исходные данные

xi	1	3	5	7	9	11
yi	34	27	22	18	17	16

Используя метод наименьших квадратов оценить гиперболическая зави-

симость y = a + bx между переменными x и y .

Решение. Результаты расчетов представлены в табл. (5.7).

												Таблица 5.7
i		xi		yi		1			1				yi
						x			x	2			x
						i			i				i
1	1		34		0,3333			0,1111				9
2	3		27		0,2			0,04				4,4
3	5		22		0,1428			0,0204				2,5714
4	7		18		0,1111			0,0123				1,8889
5	9		17		0,0909			0,0083				1,4545
6	11		16		0,3333			0,1111				9
Σ		–		134	1,8782			1,1921				53,3148

Составляем систему нормальных уравнений (5.17)

49