Практикум по высшей математике_часть 2

Пример 6.45. Вычислить приближенно интеграл I = ∫1													dx			при n =10 .
													x +	1
										0
Решение. Разделим отрезок [0;1] на 10 равных частей и составим таблицу
значений функции		f (x	) =	1			, где x = a + ∆x k			, ∆x = b − a = 0,1, k = 0,1,..., n .
		k		xk +1			k				n
								Таблица 6.1. Расчеты к примеру 6.45
	k		xk				f (xk )		k			xk					f (xk )
	0		0				1,00000		6		0,6						0,62500
	1	0,1					0,90909		7		0,7						0,58824
	2	0,2					0,83333		8		0,8						0,55556
	3	0,3					0,76923		9		0,9						0,52632
	4	0,4					0,71429		10			1					0,50000
	5	0,5					0,66667

1) По формуле прямоугольников:

I ≈ b −n a ( f (x0 ) + f (x1 ) +...+ f (x9 ))=101 (1+0,90909 +...+0,52632)=

= 0,1 7,18771=0,718771

или

I≈ b −n a ( f (x1 ) + f (x2 ) +...+ f (x10 ))=101 (0,90909 +0,83333+...+0,5)=

=0,1 6,68771=0,668771.

2)По формуле трапеции:

I ≈ b − a		f (x0 ) + f (x10 )	+ f (x ) + f (x ) +... + f (x )				=
n		2	1	2	9

	=	1			1+0,5	+0,90909 +...+0,52632		=0,1 6,93771=0,693771.
		10			2

3) Вычислим интеграл, используя формулу Симпсона. Так как отрезок [0;1] делится на 10 равных частей, то в данном случае 2n =10 или n =5 . Следо-

вательно,

I≈ b6−5a ( f (x0 ) + f (x10 ) + 2( f (x2 ) + f (x4 ) + f (x6 ) + f (x8 ))+

+4( f (x1) + f (x3 ) + f (x5 ) + f (x7 ) + f (x9 ))=

109

= 301 20,794506=0,693150 .

Вычислим заданный интеграл по формуле Ньютона – Лейбница:

I = ∫1	dx			= ln | x +1|		10 = ln 2	≈ 0,693147 .
	x +	1
0

Таким образом, наиболее точный результат получен с помощью формулы Симпсона. При этом погрешность составляет 0,000003, т.е. получен результат с пятью верными знаками.

Задания для самостоятельного решения

6.13. Используя формулу Ньютона – Лейбница, вычислить интегралы:

1)	∫1	x3dx ;
	0
3)	∫1	2x dx ;
	0

π2

5)∫ sin xdx ;

0

7) ∫1 exdx ;

0

π2

9)∫ cos xdx ;

	0
	1 2			dx
11)	∫					;
				1 − x	2
	0
13)	∫1	(1 + x −3x2 )dx ;
	−2
15)	6	x − 6 dx ;
	∫1			x
17)	∫3	(5 − 2x + x2 )dx ;
	1

π3

19)∫ tgxdx ;

	0
	21) ∫1	dx	;
		4 + 2x
	0

2)	∫3	dx	;
		1 + x2
1	3

4) ∫3 (3x2 + 2x +1)dx ;

	2
	3		dx
6)	∫2			;
		x2 −1
8)	4 ( x +1)dx					;
	∫		x	2
	1
10)	∫2 dx ;
	1		x
12)	∫1		(2x3 + ех)dx ;
	0
	2		dx
14)	∫0				;
			4 + x2
16)	∫1		(1 + x2 )dx ;
	0
18)	∫2		(1 + x3 )dx ;

−1

π3

20)∫ cos xdx ;

	0
22)	2	x +	1	dx ;
	∫1		x

110

23)	π∫/		4 ctgxdx ;	24)	π∫/		2 cos xdx ;
	π /		6		π /		4
25)	π∫/		3 cos2xdx ;	26)	∫2	2 −		2x3 +	1	dx ;
									2
	π /		4		1				x
27)	∫3	(5 + 4x + x2 )dx ;		28)	∫3		dx	;
						x +4
	1				1

29)		∫2			dx		;
	1				1 + x2
		2
31)	π 8					2x		+	π
	∫		cos						dx ;
		0							4

6.14. Используя метод замены

1)	∫e ln xdx ;
	1					x
3)	∫3					xdx		;
						2
	0					4 − x
	2	1
			exx dx2 ;
5)	∫1
	3
7)	e∫					dx			;
	1			x		1 + ln x
9)	∫e					dx				;
				x		2
	1					1 −ln		x
	3 π 4
11)			∫			x2 sin x3dx ;
		0
	π 2 3x2 −sin x
13)		∫0				x3 + cos x					dx ;

π4 cos 2xdx

15)∫0 3 +sin 2x ;

17)	∫1			x2				dx ;
				1 − x		6
	0
	π	2		4 sin			x dx ;
19)		∫			x
		0

30)	1/∫4		dx		;
			1 − x	2
	0
32)	π∫/ 4		1				dx .
			1 −16x			2
	0

переменной, вычислить интегралы:

2)	∫e (1 + ln x)dx ;
	1	x
	2 π	x−2 sin 1 dx ;
4)	∫
	1 π	x
	π 3
6)	∫	sin x cos xdx ;
	0
	π 2
8)	∫ sin2 хcos xdx ;
	0
10)	∫2 xe−x2 dx ;
	1

1	1 +xx4 dx ;
12) ∫0

π8 etg2 x

14)∫0 cos2 2x dx ;

16) ∫1 x3 2x4 dx ;

0

	4
18)	e∫	ln x	dx ;
	1	x

20) ∫e ln2 xdx ;

1 x

111

21)

∫4

dx

;

22)

∫1

dx

;

x +

5

x +

3

0

0

x

23)

∫5

dx

;

24)

∫5

dx

;

1

3x +1 +

1

1

3x +1 +1

25)

∫3

dx

;

26)

∫5

xdx

;

0

x +1 +1

1

4x +5

π 2

dx

π 2

dx

27)

∫

;

28)

∫

;

−π 2 2cos x −1

−π 2 2 +5cos x

π 4

dx

π 4

dx

29)

∫0

;

30)

∫0

;

2sin2 x + 5

2 −3sin x

π 4

dx

π 4

dx

31)

∫

;

32)

∫

.

3sin x +5cos x

1 −sin 3x

0

0

6.15. Методом интегрирования по частям вычислить интегралы:

	∫1										π 2
1)		x 4x dx ;								2)	∫ xcos xdx ;
	0										π 3
	π 2										∫2
3)	∫ xsin xdx ;									4)		x log2 xdx ;
	π 3										1
5) ∫1 x 6x dx ;										6) ∫1 x 10x dx ;
	0										0
7)	∫2	x 5x dx ;								8)	∫0		e2 x sin xdx ;
	1										−π 2
	π 2										π 3
9)	∫ e2 x cos xdx ;									10)	∫ x sin 3xdx ;
	0										0
	π		2	sin xdx ;						12)	2		ln xdx		;
11) ∫x											∫		x	4
	0										1
	3		2	log3 xdx					;	14)	e		ln xdx		;
13) ∫x											∫		x	3
	1										1
	π 3			x							1
15)	∫							dx	;	16)	∫(2x −1) 7x dx ;
					2	x
	π 4 cos										0
	e−1										π	2
17)	∫ ln(x +1)dx ;									18)	∫ (x +1)sin 2xdx ;
	0										0
19) ∫1 arccos xdx ;										20)	∫1 arcsin xdx ;
	0										0

112

		e							π 2
	21)	∫ln xdx ;						22)	∫ x2 cos xdx ;
		1							0
	23)	∫1	xarctgxdx ;					24)	∫1 arctgxdx ;
		0							0
		π 4							π 4
	25)	∫ x cos xdx ;						26)	∫ xctg2 xdx ;
		0							π 6
		π 3							1
	27)	∫ (x − 2)cos 2xdx ;						28)	∫x e2 x−1dx ;
		0							0
	29)	∫1	x arccos xdx ;					30)	∫1	x arcsin xdx ;
		0							0
		π 3		x					1
	31)	∫					dx ;	32)	∫x2arctgxdx .
					2	x
		π 4 sin							0
	6.16. Вычислить среднее значение функции y = cos x в интервале π													; π	.
													4	3
	6.17. Вычислить среднее значение функции y = ln x в интервале [1;e].
	6.18. Вычислить среднее значение функции y =									x +	1		в интервале	[1;4].
											x

6.19.Вычислить среднее значение функции y =2(1+ex )−1 на отрезке [0;2].

6.20.Используя формулы прямоугольника, трапеции и Симпсона, вычислить приближенно интеграл, разбивая интервал интегрирования на 10 частей. Используя формулу Ньютона – Лейбница, оценить полученную погрешность:

1) ∫1 x2dx ;	2) ∫2 dx2 ;	3) ∫0 (x +1)dx .
0	1 x	−1

6.21. Вычислить приближенно по правилам прямоугольника, трапеции и Симпсона, вычислить приближенно интеграл, разбивая интервал интегрирования на n частей:

	1) ∫1	1−x3 dx ( n =10 );	2) ∫5	dx		( n =6 );
				ln x
	0		2
	3) ∫1 e−x2 dx ( n =10 );		4) ∫1	arctg x dx ( n =10 ).
	0		0	x

113

ТЕМА 4

НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ

Несобственные интегралы с бесконечными пределами интегрирования

Пусть функция f (x) определена для всех x ≥a и интегрируема на любом

отрезке [a, b] ( −∞<a <b <+∞). Тогда
+∞∫	f (x)dx =blim→+∞ ∫b	f (x)dx .	(6.14)
a	a

Если предел (6.14) существует и конечен, то функция f (x) называется интегрируемой на интервале [a, +∞) , а соответствующий интеграл называется

сходящимся. Если предел не существует или равен бесконечности, то интеграл называется расходящимся.

Интеграл вида +∞∫ f (x)dx называют несобственным интегралом первого

a

рода.

Аналогично определяются несобственные интегралы первого рода на интервалах (−∞, b] и (−∞, +∞) :

∫b	f (x)dx =alim→−∞ ∫b	f (x)dx ,
−∞	a
+∞∫	f (x)dx =alim→−∞ ∫c	f (x)dx +blim→+∞ ∫b	f (x)dx ,
−∞	a	c

где c –любое действительное число.

Признаки сходимости несобственного интеграла первого рода

Признак сравнения. Пусть функции f (x) и g(x) определены для всех x ≥a и интегрируемы на каждом отрезке [a, b] и 0 ≤ f (x) ≤ g(x) для всех x ≥a .

Тогда из сходимости интеграла +∞∫ g(x)dx следует сходимость интеграла

a

+∞∫ f (x)dx , а из расходимости интеграла +∞∫ f (x)dx следует расходимость инте-

a

a

грала +∞∫ g(x)dx .

a

114

Признак абсолютной сходимости.

Пусть функция f (x) определена для

всех x ≥a . Если

интеграл

+∞∫

f (x)

dx

сходится,

то

сходится и интеграл

a

+∞∫ f (x)dx , причем

a

+∞∫ f (x)dx

≤+∞∫

f (x)

dx .

a

a

В этом случае говорят, что интеграл +∞∫ f (x)dx сходится абсолютно.

a

Если интеграл

+∞∫ f (x)dx

сходится,

а интеграл

+∞∫

f (x)

dx расходится, то

a

a

интеграл +∞∫ f (x)dx называется условно сходящимся.

a

Несобственные интегралы от неограниченных функций

Пусть функция f (x) определена для всех x [a;b) , интегрируема на лю-

бом отрезке x [a;b −ε], 0 <ε <b −a и			f (x) →∞ при x →b −0 (т.е. в точке b
функция f (x)	имеет разрыв второго рода, при этом функция неограниченна
слева в точке b ). Тогда
∫b	f (x)dx =εlim→+0 b∫−ε	f (x)dx .	(6.15)
a	a

Если предел (6.15) существует и конечен, то несобственный интеграл называется сходящимся, в противном случае – расходящимся.

Аналогично, если функция f (x) неограниченна справа в точке a , то

∫b	f (x)dx =εlim→+0 ∫b		f (x)dx .
a		a+ε
Если функция f (x)		неограниченна в окрестности внутренней точки c
отрезка x [a;b], то
∫b	f (x)dx = ∫c	f (x)dx + ∫b		f (x)dx =	εlim→+0 c∫−ε	f (x)dx + εlim→+0	∫b	f (x)dx .
a	a		c		a		c+ε

115

Несобственные интегралы от неограниченных функций называют несоб-

ственными интегралами второго рода.

Признаки сходимости несобственных интегралов второго рода аналогичны подобным признакам сходимости для несобственных интегралов второго рода.

Из признака сравнения, в частности, следует, что интеграл

b dx

∫a (b −x)α

сходится при α <1 и расходится при α ≥1.

Примеры решения задач

Пример 6.46. Вычислить несобственные интегралы или установить их расходимость:

0

dx

∞ dx

∞

dx

1) −∞∫

;

2) ∫2

;

3) −∞∫

.

1+ x

xln2 x

x2 +2x −3

Решение. 1) По определению

∫0

dx

= lim ∫0

dx

=ln |1+ x |

b0

=ln1− lim

(ln |1+b|)=−∞.

−∞1+ x

b→−∞ b 1+ x

b→−∞

Следовательно, рассматриваемый интеграл расходится.

2) Используя метод замены переменной, найдем произвольную первообразную для подынтегральной функции:

	dx		ln x =t			dt	1	1
∫		=	dx	=dt		=∫t2	=−t	=−		.
	xln2 x								ln x
			x

Тогда исходный интеграл равен

∞

dx

a

dx

1

a

1

∫

=lim

∫

=−lim

=−lim

−

2

2

a→∞

a→∞

a→∞

2

x ln

x

2

x ln

x

ln x

2

ln | a |

	1		=	1	.
	ln 2			ln 2

Так как предел существует и конечен, то соответствующий интеграл сходится.

3) Выделив в знаменателе полный квадрат, получаем

∞	dx	∞	dx	c	dx	∞	dx
−∞∫		=−∞∫		=−∞∫		+∫c
								.	(6.16)
	x2 +2x −3		(x +1)2 −4		(x +1)2 −4		(x +1)2 −4

116

В качестве точки c можно взять любую конечную точку, например, c =0 . Вычисляем первый интеграл суммы (6.16):

0

dx

0

d (x

+1)

1

(x +1)

−2

0

= lim

=

lim ln

=

−∞ (x +1)

2

−4

(x +1)

2

−2

2

2 2

(x +1)

+2

a

a

∫

a→−∞ ∫

a→−∞

1

x −1

0

1

1

a −1

=

lim ln

=

lim

ln

−

−ln

.

4

x

+3

4

3

a +3

a

a→−∞

a→−∞

Так как lim a −1 =1, то окончательно получаем

a→−∞ a +3

0	dx		1	1		1
−∞∫
		=	4 ln	3	= −	4 ln 3 .
	(x +1)2 − 4

Аналогично вычисляем второй интеграл суммы (6.16):

∞

dx

b

d (x +1)

1

x −1

b

= lim

=

lim ln

=

∫

(x +1)2

− 4

∫(x +1)2 − 22

x +3

b→∞

4 b→∞

0

0

b −1

0

=

1 lim ln

−ln

−

1

= −

1 ln 1

=

1 ln 3 .

b +3

4 b→∞

3

4 3

4

Следовательно,

	∞	dx
	−∞∫		=0 ,
		x2 +2x −3

т.е. интеграл сходится.

Пример 6.47. Вычислить интегралы от неограниченных функций или установить их расходимость:

e	dx			0		dx		3		dx
1) ∫				π∫				3) ∫
		;	2)				;				.
	x ln x				2	sin2 x			3	1−x
1				−				0

Решение. 1) Подынтегральная функция 1(xln x) неограниченна в окрестности точки x =1, но на любом отрезке [1+ε;e] , ε >0 она интегрируема. Значит

∫e

dx

=

dx

= d ln x

=

∫e

d ln x

= 2εlim→+0 ( ln x

1e+ε )=

x

1 x

ln x

1+ε

ln x

= 2εlim→+0 ( ln e −

ln(1 +ε) )= 2 .

117

Следовательно, данный интеграл сходится.

2) Подынтегральная функция sin−2 x неограниченна в окрестности точки x =0 и интегрируема на любом отрезке [−π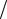2;−ε], ε >0 . Тогда

		0	dx	ε		dx			ε−π 2	= −εlim→−0 (ctgε −ctg(−π 2))=∞ .
	π∫			= εlim→−0 π∫			= −ctg x
			sin2 x		2	sin2 x
	−	2		−

Следовательно, данный интеграл расходится.

3)Подынтегральная функция 1 3 1− x неограниченна в окрестности точки

x=1, которая является внутренне точкой промежутка интегрирования. Тогда по определению

∫3		dx	= ∫1		dx	+ ∫3		dx	.	(6.17)
	3	1 − x		3	1 − x		3
0			0			1		1 − x

Вычислим каждое слагаемое отдельно.

1

dx

1−ε

dx

3

1−ε

∫0

= lim

∫0

= −

lim

3

(1 − x)

2

=

2

3

1 − x

3

1 − x

ε→+0

ε→+0

0

= − 23

εlim→+0 (3 ε2 −1)= 23 .

Аналогично вычисляем второе слагаемое равенства (6.17):

3		dx		3		dx			3						3
∫			= εlim→+0	∫				= −		εlim→+0		3	(1 − x)	2		=
									2
	3	1 − x			3	1	− x
1				1+ε											1+ε

= − 32 εlim→+0 (3 4 − 3 ε2 )= − 32 3 4 .

Подставив найденные значения в равенство (6.17), получаем

	3	dx	= 23	(1 − 3 4 ).
	∫0
		3 1 − x
	Интеграл сходится.			4
					dx
	Пример 6.48. Исходя из определения вычислить интеграл ∫1					или
					(x − 2)2

доказать его расходимость.

Решение. Подынтегральная функция (x −2)−2 неограниченна в окрестности точки x = 2 . Тогда по определению несобственного интеграла второго рода

118