Практикум по высшей математике_часть 2

yo.o. = C1ek1x +C2ek2x .

2) Корни характеристического уравнения (7.32) действительны и одинаковы k = k1 = k2 = − p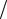2 (дискриминант D квадратного уравнения (7.32) равен

нулю). Тогда общее решение линейного однородного уравнения (7.30) имеет вид:

yo.o. = (C1 +C2 x)ekx .

3) Корни характеристического уравнения (7.32) – комплексные, т.е. D < 0 , k1 =α +iβ , k2 =α −iβ . Тогда

yo.o. = eαx (C1 sin βx +C2 cos βx) .

Общее решение уo.н. линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами y′′+ py′+ qy = f (x) равно сумме yo.o. общего решения соответствующего однородного уравнения y′′+ py′+ qy = 0 и какого-нибудь частного решения yч.н. неоднородного уравнения, т.е.

уo.н. = yo.o. + yч.н. .

(7.33)

Вычисление частного решение неоднородного уравнения в общем случае при произвольных f (x) достаточно сложная задача. Рассмотрим способы на-

хождения частного решения в следующих случаях:

− правая часть уравнения (7.29) является многочленом, т.е.

f(x) = Pn (x) = a0 + a1x + a2 x2 +... + an xn ;

−правая часть уравнения (7.29) имеет вид

f(x) = aeαx ;

−правая часть уравнения (7.29) имеет вид

f(x) = asin βx +bcos βx ;

−правая часть f (x) уравнения (7.29) есть алгебраическая сумма выше-

перечисленных функций.

Рассмотрим все указанные случаи.

Случай I. Правая часть уравнения (3.29) – многочлен.

1) если k1 ≠ 0, k2 ≠ 0 , то частное решение находим в виде многочлена той же степени

yч.н. = А0 + А1x + А2 x2 +... + Аn xn ;

168

2) если один из корней соответствующего характеристического уравнения равен нулю, то

yч.н. = x(А0 + А1x + А2 x2 +... + Аn xn );

3) если оба корня характеристического уравнения равны нулю, то

yч.н. = x2 (А0 + А1x + А2 x2 +... + Аn xn ).

Случай II. Правая часть уравнения (3.29) – показательная функция

f(x) = aerx .

1)если корни характеристического уравнения k1 ≠ r, k2 ≠ r , то частное решение ищем так же в виде показательной функции

yч.н. = Aerx ;

2) если k1 = r или k2 = r , то

yч.н. = Axerx ;

4)если k1 = k2 = r , то

yч. р. = Ax2erx .

Случай III. Правая часть уравнения (3.29) – тригонометрический полином

f(x) = asin βx +bcos βx ;

1)если ±iβ не является корнями соответствующего характеристического уравнения, то частное решение ищем в виде тригонометрического полинома

yч.н. = Asin βx + B cos βx ;

2) если ±iβ являются корнями соответствующего характеристического уравнения, то частное решение ищем в виде

yч.н. = x(Asin βx + B cos βx).

После выбора соответствующего частного решения, подставляем yч.н. и

его производные в уравнение (7.29). Затем, используя метод неопределенных коэффициентов, находим неизвестные коэффициенты.

169

Примеры решения задач

Пример 7.17. Найти общее решение дифференциального уравнения y′′− y′− 2 y = 2x +5 .

Решение. Находим общее решение yo.o. соответствующего однородного уравнения y′′− y′− 2 y = 0 . Характеристическое уравнение

k 2 − k − 2 = 0

имеет различные действительные корни k1 = 2, k2 = −1. Тогда общее решение однородного уравнения есть

yo.o. =C1e−x +C2e2 x .

Теперь находим частное решение исходного неоднородного уравнения. Так как правая часть уравнения есть многочлен первой степени и ни один из корней характеристического уравнения не равен нулю, то

yч.н. = Ax + B .

Подставляем yч.н. и его производные yч′.н. = A, yч′′.н. = 0 в исходное уравне-

ние:

−A − 2(Ax + B) = 2x +5 или −2 Ax +(−A − 2B) = 2x +5 .

Приравниваем коэффициенты при одинаковых степенях переменной x :

x		−2A = 2,		A = −1,
x0		−A − 2B = 5,		B = −2.

Следовательно, частное решение исходного неоднородного уравнения

есть

yч.н. = −x − 2 .

По формуле (7.33) составляем общее решение неоднородного уравнения как сумму общего решения соответствующего однородного уравнения и частного решения исходного неоднородно уравнения:

уo.н. = C1e−x +C2e2 x − x − 2 .

Пример 7.18. Найти общее решение дифференциального уравнения y′′− 2 y′ = −6x2 −1.

Решение. Составляем характеристическое уравнение k 2 − 2k = 0

170

и находим его корни: k1 = 2, k2 = 0 . Следовательно, частное решение однородного уравнения есть

yo.o. = C1 +C2e2 x .

Так как правая часть уравнения – многочлен второй степени и ноль – корень характеристического уравнения, то

yч.н. = x(Ax2 + Bx +C )= Ax3 + Bx2 +Cx .

Находим частные производные:

yч′.н. =3Ax2 + 2Bx +C, yч′′.н. = 6 Ax + 2B .

Подставляем их вместе с yч.н. в исходное уравнение: 6Ax + 2B − 2(3Ax2 + 2Bx +C )= −6x2 −1

или

−6 Ax2 + x(6 A − 4B)+ 2(B −C )= −6x2 −1.

Приравниваем коэффициенты при одинаковых степенях переменной x :

x2		−6 A = −6,	A =1,
x		6A − 4B = 0,	B = 3	,
x0		2(B −C )= −1,	2
			C = 2.

Следовательно, частное решение исходного неоднородного уравнения имеет вид:

yч.н. = Ax3 + Bx2 +Cx = x3 + 32 x2 + 2x .

Общее решение неоднородного уравнения находим как сумму yo.o. и yч.н. :

уo.н. = C1 +C2e2 x + x3 + 32 x2 + 2x .

Пример 7.19. Найти	общее решение дифференциального уравнения
y′′+ 4 y′+ 4 y = f (x) , если: а)	f (x) = 98e5 x ; б) f (x) = 6e−2 x .
Решение. а) Находим корни характеристического уравнения:
k 2 + 4k + 4 = 0, k = k		2	= −2 .
	1

171

Так как корни характеристического уравнения равны, то общее решение однородного уравнения есть

yo.o. = (C1 +C2 x)e−2 x .

Определяем вид частного решение неоднородного уравнения. Правая часть уравнения – показательная функция и ни один из корней характеристического уравнения не равен r = 5 , то

yч.н. = Ae5 x

и

yч′.н. = 5Ae5 x , yч′′.н. = 25Ae5 x .

После подстановки в исходное уравнение, получаем

25Ae5 x + 4 5Ae5 x + 4Ae5 x = 98e5 x

или

49 Ae5 x = 98e5 x , 49 A = 98 A = 2 .

Следовательно,

yч.н. = 2e5 x

и

yo.н. = (C1 +C2 x)e−2 x + 2e5 x .

б) Пусть теперь f (x) = e−2 x . Общее решение однородного уравнения было найдено в предыдущем случае. Определяем вид частного решения неоднородного уравнения. Так как f (x) = e−2 x и оба корня характеристического уравнения равны r = −2 , то

yч.н. = Ax2e−2 x .

Тогда

yч′.н. = 2Axe−2 x − 2 Ax2e−2 x , yч′′.н. = 4Ax2e−2 x −8Axe−2 x + 2 Ae−2 x .

После подстановки в исходное уравнение, получаем

4Ax2e−2 x −8Axe−2 x +2Ae−2 x +4(2 Axe−2 x −2Ax2e−2 x )+4 Ax2e−2 x =6e−2 x

или

2Ae−2 x = 6e−2 x , 2 A = 6 A = 3 .

Следовательно, yч.н. =3x2e−2 x и yo.н. = (C1 +C2 x)e−2 x +3x2e−2 x .

172

Пример 7.20. Найти	общее решение	дифференциального уравнения
y′′+ 4 y′+5 y = 65cos 2x .
Решение. Характеристическое уравнение
k 2 + 4k +5 = 0 .
имеет комплексные корни ( D =−4 =(2i)2 , где i		– мнимая единица (см. прило-
жение)) вида k1,2 =−2 ±i , т.е.	a =−2, β =1. Тогда общее решение однородного
уравнения есть

yo.o. = e−2 x (C1 cos x +C2 sin x).

Правая часть исходного уравнения – тригонометрический полином, следовательно,

yч.н. = Acos 2x + Bsin 2x .

и

yч′.н. = −2 Asin 2x + 2B cos 2x, yч′′.н. = −4Acos 2x − 4Bsin 2x .

Подставляем yч.н. и его производные в исходное уравнение:

−4 Acos 2x − 4Bsin 2x + 4(−2 Asin 2x + 2Bcos 2x)+ +5(Acos 2x + Bsin 2x) = 65cos 2x .

Отсюда

(A +8B)cos 2x +(−8A + B)sin 2x = 65cos 2x .

Составляем систему уравнений для определения неизвестных коэффициентов A и B . Дляэтогоприравниваемкоэффициентыприодноименныхфункциях:

cos 2x		A +8B =1,		A =1,
sin 2x		−8A + B = 0,		B =8.

Значит, частное решение исходного неоднородного уравнения есть

yч.н. = cos 2x +8sin 2x .

Следовательно,

yo.н. = e−2 x (C1 cos x +C2 sin x)+ cos 2x +8sin 2x .

173

Пример 7.21. Найти частное решение уравнения y′′−3y′ = x +cos x , удов-

′	= −	1
летворяющее начальным условиям y(0) = 0, y (0)		9 .

Решение. Составляем характеристическое уравнение для соответствующего однородного линейного дифференциального уравнения:

k 2 −3k = 0 .

Его корни k1 = 0 , k2 = 3, следовательно, общее решение однородного уравнения

yo.o. = C1 +C2e3x .

Правая часть исходного уравнения есть сумма двух функций f1(x) = x и f2 (x) = cos x . Частное решение соответствующее правой части f1 (x) = x , нужно искать в виде (Aх+ В)x , т.к. f1(x) – многочлен первой степени и ноль является

корнем характеристического уравнения. Частное решение, соответствующее f2 (x) = cos x , ищем в виде Сcos x + Dsin x . По принципу наложения частных

решений

yч.н. = Ax2 + Вx +Сcos x + Dsin x .

Находим производные первого и второго порядков:

yч′.н. = 2Ax + В−Сsin x + D cos x ; yч′′.н. = 2A −Сcos x − Dsin x .

Подставив их в исходное уравнение, получаем

2A −Сcos x − Dsin x −6 Ax −3B +3C sin x −3D cos x = x + cos x ,

−6 Ax +(2A −3B)+(−С −3D)cos x +(3C − D)sin x = x + cos x .

Приравнивая коэффициенты при одноименных функциях и одинаковых степенях переменной x , составляем систему и находим ее решение:

x		−6A =1,		A = −	1		B = −	1
x0		2 A −3B = 0,			6 ,			9 ,
cos x		−3D −C =1,		D = −		3	, C = −		1	.
sin x		3C − D = 0,			10
								10

Выписываем общее решение неоднородного уравнения:

y	о.н.	= C +C	e3x −	x	−	x2	−	1	cos x −	3	sin x .	(7.34)
		1 2	9		6		10		10

174

Для нахождения частного решения, удовлетворяющего начальным усло-

виям y(0) = 0, y′(0) = −19 , найдем производную функции (7.34):

y′ = 3C2e3x −	1	−	x	+		1	sin x −		3	cos x .	(7.35)
	9				10			10
		3

Подставляем x = 0 в (7.34) и в (7.35), получаем систему для вычисления неизвестных постоянных:

C1 +C2 −101 = 0,

3C2 − 19 −103 = −19 .

Решение системы дает следующие значения постоянных – C2 = 101 и

C1 = 0 . Значит, искомое частное решение есть

y	=	1		e	3x	−	x	−	x2	−	1		cos x −	3		sin x .
ч.н.		10					9		6		10			10

Задания для самостоятельного решения

7.8.

Найти общие или частные решения дифференциальных уравнений:

1)

y/// =

6

, если y = 2, y/ =1,

y// =1 при x =1;

x3

2)

y// =

1

, x =

π , y(x )

= ln 2 , y/ (x ) =

1;

cos2 x

0

4

0

2

0

3)

x3 y//

+ x2 y/ =1;

4)

y// = 4cos 2x ;

5)

y// + y/ tgx = sin 2x ;

6)

y// =

1

;

1 + x2

7)

y// xln x = y/ ;

8) yy// + y/ 2 = 0 ;

9)

y// tgy = 2( y/ )2 ;

10)

y// + 2 y( y/ )3 = 0 ;

11) (1 + x2 ) y//

+ 2xy/

= x3 ;

12)

y// y3

=1;

13) 2 yy// = ( y/ )2 ;

14)

2xy//

+ y/

= ln x .

7.9.Найти общее решение дифференциальных уравнений:

1)	y// − 4 y/ + 4 y = 0 ;	2)	y// − 4 y/ +13y = 0 ;
3)	y// − 4 y = 0 ;	4)	y// − 4 y/ +3y = 0 ;
5)	y// − 2 y/ + y = e2 x ;	6)	y// + 4 y/ = x2 + 2x −1;

175

7)	y// − 4 y =8x3 ;	8)	y// +3y/ + 2 y = sin 2x + 2cos 2x ;
9)	y// + y = x + 2ex ;	10)	y// +3y/	= 9x ;
11)	y// −3y/ + 2 y = ex ;	12)	y// − 2 y = xe−x ;
13)	y// − y/ − 2 y = sin 3x ;	14)	y// − y/ −6 y = e2 x ;
15)	y// − 4 y/ = х2 + 2 ;	16)	y// + 4 y/	+13y = 2cos3x ;
17)	y// +16 y = sin 4x ;	18)	y// −3y/	+ 2 y = x2 +3x +5;
19)	y// + 4 y/ +3y = 5e3x ;	20)	y// − 4 y/	+3y =3sin x + cos x ;
21)	y// − 2 y/ −3y = 2sin 2x ;	22)	y// + 2 y/	−3y = 2x2 +3x −1;
23)	y// +5 y/ = 5x2 − 2 ;	24)	y// − 2 y/	+5y = 2e2 x+1 ;
25)	y// + 2 y/ +5y = sin 4x ;	26)	y// + 2 y/	+10 y = 4cos5x ;
27)	y// + 2 y/ −10 y = 5e5 x ;	28)	y// + 4 y/	+13y = 3x2 − 2x ;
29)	4 y// −9 y/ = х2 + x ;	30)	9 y// + 25y = 2cos5x .

7.10. Найти частные решения дифференциальных уравнений:

1)y// −6 y/ +9 y = 9x2 −39x + 65, y(0) =1, y/ (0) =1;

2)4 y// +16 y/ +15 y = 4e−3x2 , y(0) = 3, y/ (0) = −5,5 ;

3)y// − 4 y/ + 20 y =16xe2 x , y(0) =1, y/ (0) = 2 ;

4)y// − 2 y/ +37 y = 36cos6x, y(0) = 0, y/ (0) = 6 .

7.11. Найти		общее	решение		дифференциального	уравнения
2 y// + 4 y = f (x) , если функция f (x) равна:
1)	f (x) = x2 −2x +3;		2)	f (x) =5e3x ;
3)	f (x) =3cos 2x ;		4)	f (x) = x2 sin x ;
5)	f (x) =tgx ;		6)	f (x) = xex .
7.12. Найти		общее	решение		дифференциального	уравнения
5 y// +5y = f (x) , если функция			f (x) равна:
1)	f (x) = x2 +4x −1;		2)	f (x) =3ex ;
3)	f (x) =2cos x ;		4)	f (x) =ex (x2 + x) .
7.13. Найти		общее	решение		дифференциального	уравнения
y// + y/ = f (x) , если функция			f (x) равна:
1)	f (x) =2x2 −3;		2)	f (x) =3cos7x ;
3)	f (x) = x(sin x +cos x);		4)	f (x) =ex sin x .

176

РАЗДЕЛ 8

РЯДЫ

ТЕМА 1

ЧИСЛОВЫЕ РЯДЫ Основные определения

Пусть дана числовая последовательность a1, a2 , a3 ,..., an ,.... Выражение вида

∞
a1 + a2 + a3 +... + an +... = ∑an	(8.1)
n=1
называется числовым рядом или просто рядом. Числа a1, a2 ,..., an ,...	называются

членами ряда, число an с общим номером n называется общим членом ряда. Суммы конечного числа первых членов ряда

S1 = a1, S2 = a1 + a2 , S3 = a1 + a2 + a3 ,..., Sn = a1 + a2 + a3 +... + an ,...

называются частичными суммами ряда (8.1). Так как число членов ряда бесконечно, то частичные суммы образуют бесконечную числовую последовательность

S1, S2 , S3 ,..., Sn ,....

(8.2)

Ряд (8.1) называется сходящимся, если последовательность (8.2) его частичных сумм сходится к некоторому числу S . В этом случае число S называется суммой ряда (8.1). В противном случае ряд (8.1) называется расходящимся. В случае сходимости ряда (8.1) его сумму записывают в виде символического равенства

∞

S = a1 + a2 + a3 +... + an +... или S = ∑an .

n=1

Необходимый признак сходимости числового ряда

Если числовой ряд (8.1) сходится, то предел его общего члена равен нулю:

lim a	n	= 0 .	(8.3)
n→∞

177