Практикум по высшей математике_часть 2

Потенцируем последнее равенство:

y + 2 = Cesin x или y = Cesin x − 2 .

Пример 7.6. (Задача об эффективности рекламы.) Некоторая торговая фирма рекламирует реализуемую продукцию. В момент времени t0 = 0 о про-

дукции из рекламы получили информацию x0 человек из общего числа N по-

тенциальных покупателей. Затем информация о товаре распространяется посредством общения людей. Предполагая, что число встреч для передачи информации за время ∆t пропорционально количеству людей, уже владеющих этой информацией; количеству людей, не владеющих информацией, и промежутку времени ∆t , определить закон распространения сообщения во времени.

Решение. Пусть число людей, владеющих информацией в момент времени t > 0, равно y(t) . Тогда, согласно условию задачи, число людей ∆y полу-

чающих информацию за промежуток времени ∆t определяется равенством

∆y = k y (N − y) ∆t ,				(7.10)
где k – коэффициент пропорциональности, k > 0 .
Разделим обе части равенства (7.10) на ∆t				и перейдем к пределу при
∆t → 0 :
lim	∆y = ky(N − y) y′ = ky(N − y) .
∆t→0	∆t
Получили уравнение с разделяющимися переменными.
Разделяем переменные:
dy = ky(N − y)		dy	= kdt .
		y(N − y)
dt

Интегрируя левую и правую части последнего равенства, находим общее решение дифференциального уравнения:

∫ y(Ndy− y) = ∫kdt .

Вычислим интеграл, стоящий в левой части последнего равенства. Так как подынтегральная функция является правильной рациональной дробью, то с помощью метода неопределенных коэффициентов раскладываем ее на сумму простейших дробей:

1	=	A	+	B	=	A(N − y)+ By	,
y(N − y)		y		N − y		y (N − y)

148

A(N − y)+ By =1,
y1		−A + B = 0,	A = B =	1	.
y0		AN =1,
				N

Отсюда

dy

1

1

dy

1

(ln y −ln (N − y))=

1

y

=

+

dy =

ln

.

∫ y(N − y)

N ∫

N

N − y

y N − y

N

Тогда для общего решения исходного дифференциального уравнения получаем:

N1 ln N y− y = kt + ln | C | ln N y− y = ln | CeNkt |

или

y	= Ce	Nkt	y =	N CeNkt	.
N − y				1 +CeNkt

Наконец, разделив числитель и знаменатель дроби, стоящей в правой части последнего равенства на CeNkt , находим

	y =				N	, C	=	1		(7.11)
		1		+C e−Nkt				C
						1
					1
	Постоянную C1				можно найти из начального условия y(0) = y0 .

Функция (7.11) называется логистической, а ее график – логистической кривой.

С помощью логистической функции можно описать многие экономические, социальные, технологические и биологические процессы, например, постоянный рост продаж, распространение слухов, распространение технических новшеств, рост популяции определенного вида животных и др.

Однородные дифференциальные уравнения

Уравнение вида

y′ =		y
	f			(7.12)
		x

называется однородным дифференциальным уравнением.

149

Уравнение (7.12) приводят к уравнению с разделяющимися переменными с помощью подстановки y = ux , где u =u(x) – новая искомая функция. Про-

дифференцировав равенство y = ux по переменной x , получаем:

	dy = x du			+u .	(7.13)
	dx	dx
Подставляем выражения y = ux и (7.13) в уравнение (7.12), получаем
	x du +u = f (u) .
	dx
Отсюда
	du		− dx = 0 .		(7.14)
	f (u) −u
				x

Полученное уравнение является уравнением с разделяющимися переменными. Найдя общее решение уравнения (7.14), получим общее решение исход-

ного уравнения (7.12), заменив u на xy .

Пример 7.7. Найти общий интеграл уравнения xy′ = 3y − x . Решение. Поделив обе части уравнения на x , получаем:

y
y′ = 3 x	−1,	(7.15)

т.е. уравнение (7.15) – это однородное уравнение.

Для решения уравнения (7.15) вводим новую переменную u(x) = y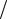 x .

Тогда y = ux и y′ = x dudx +u . После соответствующей подстановки уравнение

(7.15) принимает вид:

x dudx +u = 3u −1,

или

xdu = (2u −1)dx .

Таким образом, получили уравнение с разделяющимися переменными. Следовательно,

du	= dx		du	=	dx	1 ln | 2u −1|= ln | x | +ln C ,
2u −1 x		∫(2u −1)			∫ x	2	1

ln | 2u −1|= ln | Cx2 |, C = C12

150

или

2u −1 = Cx				2	u =	Cx2 +1	.
						2
Заменяем в последнем равенстве u на								y	:
								x
	y	=	Cx2 +1		y =	Cx3 + x	.
	x		2			2

Пример 7.8. Найти общее решение уравнения

(y2 − xy)dx +(x2 − 2xy)dy = 0 .

Решение. Преобразуем данное уравнение, разделив предварительно обе

его части на выражение (x2 − 2xy)dx :

y

y

2

y′ =

xy − y2

или

y′ =

x

−(

x

)

.

y

x

2

− 2xy

1

− 2

x

Полученное уравнение есть однородное уравнение первого порядка. Для его решения используем замену u = y x или ux = y . Тогда

u′x +u = u −u2 . 1 − 2u

Разделяем переменные:

′

u −u2

du

u2

u x

=

1 − 2u −u ,

x dx

=

.

1 − 2u

Обе части последнего уравнения делим на

xu2

, считая, что u ≠ 0 :

1 − 2u

1 − 2u

dx

∫

1 − 2u

∫

dx

1

2

2

du =

2

du =

−

du =ln | x | +ln | C |

u

x

u

x

2

∫ u

u

или

−u1 − 2ln u = ln Cx u1 + ln Cxu2 = 0 .

Возвращаемся к старой переменной, подставив в последнее равенство выражение u = y x :

151

x

y 2

Cy 2

+ ln

Cx

= 0 x + y ln

= 0 .

y

x

x

Данное решение найдено в предположении, что u ≠ 0 . Если u = 0 ,

то

y

′

x = 0 , значит y = 0 и y

= 0 . Подставив

y

= 0

в первоначальное уравнение, по-

лучим верное равенство. Следовательно,

y = 0

тоже является решением данно-

го уравнения. Следовательно, общее решение исходного уравнения

x + y ln

Cx−1 y2

= 0, y = 0 .

Линейные уравнения первого порядка

Уравнение вида

y′+ P(x)y = Q(x) ,

(7.16)

где P(x) и Q(x)

– некоторые заданные непрерывные функции, называется ли-

нейным дифференциальным уравнением

первого порядка. Если Q(x) ≡ 0 ,

то

уравнение называется однородным. Если Q(x) ≡ 0 , то дифференциальное урав-

нение (7.16) называется неоднородным.

Для решения линейного дифференциального уравнения можно использовать метод Бернулли или метод вариации произвольных постоянных. Рассмот-

рим эти методы.
			Метод Бернулли. Решение дифференциального уравнения (7.16) ищем в
виде			произведения		y = u v двух функций u = u(x)	и v = v(x) . Тогда
y	′	′	′
		=u v +uv и уравнение (7.16) принимает вид
			′	′	+ P(x)uv = Q(x)
			u v +uv
или
			v(u′+ P(x)u)+uv′ = Q(x) .			(7.17)

В качестве функции u = u(x) берут функцию, для которой выполняется равенство u′+ P(x)u = 0 . Тогда

		′		du	du
	u		= −P(x)u, dx = −P(x)u,		u = −P(x)dx,
	∫du			= −∫P(x)dx, ln | u |= −∫P(x)dx, u = e−∫P(x)dx .
			u

152

Подставим найденное значение в уравнение (7.17), при этом учитываем,

что u′+ P(x)u = 0 :

′		−∫P(x)dx		dv		∫P(x)dx
v	e		= Q(x),	dx	= Q(x) e		,

dv = Q(x) e∫P(x)dxdx, v = ∫Q(x) e∫P(x)dxdx +C ,

где C – произвольная постоянная.

Окончательно получаем решение дифференциального уравнения (7.16):

	∫Q(x) e	∫P(x)dx		e	−∫P(x)dx	.
y =			dx +C

Метод вариации произвольных постоянных. Предположим, что правая часть уравнения (7.16) равна нулю, т.е. решаем соответствующее однородное уравнение

	′		dy		dy
y		+ P(x)y = 0, dx		= −P(x)y,	y = −P(x)dx ,
∫dy			= −∫P(x)dx,	y = Ce−∫P(x)dx ,		(7.18)
		y

где C – произвольная постоянная.

Для решения исходного уравнения, предположим, что произвольная постоянная C в последнем равенстве (7.18) есть некоторая функция от переменной x . При этом решение уравнения (7.16) будем искать в виде

y = C(x)e−∫P(x)dx .

(7.19)

Тогда

y

′

′

−∫P(x)dx

−∫P(x)dx ′

=

= C (x)e

+C(x) e

′

−∫P(x)dx

′

e

−∫P(x)dx

= C (x)e

+C(x)(−∫P(x)dx)

=

′

−∫P(x)dx

+C(x) P(x)e

−∫P(x)dx

.

= C (x)e

Подставив функцию (7.19) и ее производную в исходное уравнение, получаем:

C′(x)e−∫P(x)dx − P(x) C(x)e−∫P(x)dx + P(x) C(x)e−∫P(x)dx = Q(x)

153

или

C′(x)e−∫P(x)dx = Q(x), C(x) = ∫Q(x)e∫P(x)dxdx +C1 ,

где C1 – некоторая константа.

Окончательно решение дифференциального уравнения (7.16) принимает

вид:

	∫Q(x) e	∫P(x)dx	dx +C1		e	−∫P(x)dx	,
y =

который совпадает с раннее полученным по методу Бернулли решением.

Примеры решения задач

Пример 7.9. Найти общее решение уравнения y′− 2xy = ex2 .

Решение. 1) Решим уравнение, используя метод Бернулли. y = u(x) v(x) , тогда y′ =u′v +uv′ и уравнение принимает вид

u′v +uv′− 2xuv = ex2

или

v(u′− 2xu)+uv′ = ex2 .

Пусть

(7.20)

Решая уравнение u′− 2xu = 0 , находим его простейшее частное решение:

du			= 2xu,				du = 2xdx,	∫du	= 2∫xdx,	ln | u |= x2 , u = ex2 .
dx							u	u
Подставив				найденное значение					u = ex2	в уравнение (7.20), где
u′− 2xu = 0 , получим уравнение
e	x2		′	= e	x2	,
		v

из которого находим

v′ =1, dv = dx, v = x +C .

Итак, общее решение исходного уравнения имеет вид:

y= u v = ex2 (x +C) .

2)Найдем общее решение исходного уравнения по методу вариации произвольной постоянной. Решаем однородное уравнение, соответствующее исходному

154

y′− 2xy = 0,	dy	= 2xy,	dy	= 2xdx,	∫dy	= 2∫xdx,
	dx		y		y

ln | y |= x2 + ln C, y = Cex2 .

Предположим, что C = C(x) . Тогда решение уравнения будем искать в виде функции y = C(x)ex2 . Следовательно, y′ = C′(x)ex2 + 2x C(x)ex2 и исходное уравнение принимает вид:

′

x2

+

2x C(x)e

x2

− 2xC(x)e

x2

= e

x2

C (x)e

или

dC(x)

′

x2

x2

′

C (x)e

= e

, C (x) =1,

=1, dC(x) = dx .

dx

Из последнего равенства C(x) = x +C1 .

Тогда общее решение исходного уравнения есть функция вида

y = ex2 (x +C ) .

1

Пример 7.10.

Найти

частное

решение уравнения

x2 y′ = x2 + (2x −1) y ,

удовлетворяющее начальному условию y(1) = 2 .

Решение. Преобразуем исходное уравнение, предварительно разделив обе

его части на x2 :

y

′

+

1 − 2x

y =1.

x2

(y

Полученное

линейное

уравнение решаем

с помощью замены y = uv

′

′

′

=u v +uv ). Подставив новые переменные в уравнение, получим

′

′

+

1 − 2x

uv =1

или

u v +uv

x2

1 − 2x

′

′

=1.

(7.21)

u v +u

v +

x

2

v

Предполагая, что выражение, стоящее в скобках, равно нулю, находим

′

1 − 2x

dv

2x −1

dv

2x −1

v

+

x2

v = 0 или

dx =

x2

v

v =

x2

dx ,

155

∫

dv

∫

2x −1

∫

2

1

1

=

2

dx ln | v |=

−

dx ln | v |= 2ln | x | +

.

v

x

x

2

x

x

Отсюда

1							1			1
ln	v	= ln x2 + ln ex		ln	v	= ln ex		x2		v = ex	x2 .

Подставим найденное значение переменой v =v(x) в уравнение (7.21):

1

′

1

du

1

e

x

x

2

u

1

e

x

x

2

=1 du = e

−x

x

−2

dx ,

=

dx

∫

∫

− 1

−2

∫

−1

1

− 1

du =

e x

x dx u =

e x d

x

+C .

−

= e x

− 1

1

1

Тогда y = uv = e

x

+C x2ex

= 1 +Cex

x2 и, следовательно, общее реше-

ние уравнения есть

yо. р. =

1

1

+Cex

x2 .

Учитывая начальное условие, находим

y(1) =1 +Ce = 2 Ce =1, С = е−1 .

Тогда частное решение, удовлетворяющее данному начальному условию,

имеет вид:

yч. р. =

1

1

−1

1

+ e−1ex

x2

= 1 + ex

x2 .

Пример 7.11. Найти общее решение уравнения y′

=

1

.

2x − y2

Решение. Так как y′x =

1

, то исходное уравнение принимает вид:

′

xy

x′y

= 2x − y2 .

Полученное уравнение является линейным и может быть решено с помощью замены переменной вида x( y) = u( y) v( y) . Тогда

156

′

′

2

u v

+uv − 2uv = −y

или

2v) = −y

′

′

−

2

.

(7.22)

u v

+u (v

′

Выбираем функцию v( y) такой, что v − 2v = 0 . Тогда

dv

= 2v dv = dy

1 ln | v |= y ln | v |= 2 y v = e2 y .

dy

2v

2

Из (7.22) получаем

′

2 y

2

2 y du

2

−2 y

2

u e

= −y

e

dy

= −y

du = −e

y

dy .

Отсюда

∫du = −∫e−2 y y2 dy .

Дважды используя формулу интегрирования по частям, вычислим интеграл, стоящий в правой части последнего равенства:

∫e−2 y y2 dy =

u = y2 ,

dv = e−2 y dy

= −

1 y2e−2 y + ∫e−2 y y dy =

du

= 2 ydy, v =−

1

−2 y

2 e

2

dv = e−2 y dy

1 2

−2 y

u = y ,

1

−2 y

1

−2 y

= −

2 y

e

+

du = dy, v =−

1

−2 y

−

2 ye

+

2 ∫e

dy =

2 e

= −

1

2

e

−2 y

−

1

ye

−2 y

−

1

e

−2 y

+C = −e

−2 y

2 y2 + 2 y +1

+C .

2

y

2

4

4

Тогда

u( y) = −∫e

−2 y

y

2

dy = e

−2 y

2 y2 + 2 y +1

+C .

4

Окончательно, получаем

x( y) = e

2 y

−2 y

2 y2

+ 2 y +

1

e

4

+С

или

x( y) = Ce2 y +

2 y2 + 2 y +1 .

4

157