Практикум по высшей математике_часть 2

4

dx

2

4

dx

∫1

= ∫1

dx

+ ∫2

.

(x − 2)2

(x − 2)2

(x − 2)2

Так как

2−ε

2

dx

2−ε

dx

1

− 1

1

∫

= lim

∫

= − lim

= − lim

+

= ∞

2

2

(x − 2)

ε→+0

(x − 2)

ε→+0

x − 2

ε→+0

ε

1

1

1

и

4

4

dx

4

dx

1

1 −

1

=∞,

∫

= lim

∫

= − lim

= − lim

2

2

(x − 2)

ε→+0

(x − 2)

ε→+0

x − 2

ε→+0

2

ε

2

2+ε

2+ε

то исходный интеграл расходится.

Заметим, что формальное применение формулы Ньютона – Лейбница к данному интегралу, привело бы к неверному результату:

4	dx			1			4		1			3	.
			= −					= −		+1	= −
∫1 (x − 2)		2		x − 2					2			2
							1

Пример 6.49. Исследовать на сходимость интеграл Дирихле

∞ dx I =∫1 xα .

Решение. Первообразная функции 1 xα зависит от значения параметра α . 1) Пусть α =1 , тогда

I = ∞∫dx	= limb→∞	∫b	dx	= limb→∞(ln x		1b )= limb→∞ (ln b −ln1)=∞ .
			x
1 x		1

Интеграл расходится.

2) Предположим, что α <1. Тогда

I =lim b

dx

=lim

x−α+1

b =

1

lim

(

x1−α

)

b =

1

lim

(

b1−α −1

=∞.

b→∞ ∫1

xα

b→∞

−α +1

1−α b→∞

1

1−α b→∞

)

1

Интеграл расходится. 3) Наконец, пусть α >1 .

b

dx

x−α+1

b

1

1

b

I = limb→∞

∫

α = limb→∞

=

limb→∞

=

α−1

1

x

−α +1

1

1 −α

x

1

=

1

lim

1

−1

=

1

(0 −1)=

1

.

1

α−1

α −1

α −1

−α b→∞ b

Интеграл сходиться.

119

Таким образом, интеграл Дирихле сходится, если α ≤1 и расходится, если

α >1 .

Задания для самостоятельного решения

6.22. Вычислить интегралы с бесконечными пределами интегрирования

или установить их расходимость:

1)

+∞∫

dx

;

2)

+∞∫

dx

;

3

1

x

1

x

3)

+∞∫

dx

;

4)

−∫1

dx

;

3 2

3 2

1

x

−∞

x

5)

+∞∫exdx ;

6)

−∫1 dx2 ;

0

−∞ x

7)

+∞∫

dx

;

8)

+∞∫ xe−x2 dx ;

1 + x

2

1

0

9)

∫0

xe−x2 dx ;

10)

+∞∫

x

dx ;

x

4

+1

−∞

1

11)

+∞∫

x2

dx ;

12)

+∞∫

dx

;

3

2

1

1 + x

1

4x

−

1

13)

∫0

x

dx ;

14)

∫0

x

3

dx ;

(x

2

4)

3

4

+ 3

−∞

+

−∞

x

15)

∫0

dx

;

16)

+∞∫

dx

;

4

4

−∞ 3 (x +8)

0

7 + x

+∞

2

+∞

dx

17)

−∞∫

arctg1 + x2xdx ;

18)

−∞∫

;

3 x5

19)

+∞∫e−2 xdx ;

20)

+∞∫

dx

.

1 − x

2

−∞

∞

6.23. Вычислить интегралы от неограниченных функций или установить их расходимость:

	2	dx		4	dx
	1) ∫1		;	2) ∫2		;
		4 − x2			(2 − x)2

120

3)

∫1

dx

;

4)

∫2 ln(x −1)dx ;

3

−1

1 − x

1

x −1

5)

∫1

dx

;

6)

∫2

dx

;

3

1 − 2x

2

0

0 3 (1− x)

7)

∫4

dx

;

8)

∫1

dx

;

2

2

1 3 (x −3)

0 (1 − 2x)

1

2хdx

e

dx

9)

∫0

;

10) ∫0

;

1 − х4

xln2 x

π

cos xdx

12) ∫2

11) ∫2

;

хdx

.

6

4 − х

2

0

(1 −sin х)

0

6.24. Вычислить интегралы или установить их расходимость:

1)	+∞∫ x cos x2dx ;
	0
3)	+∞∫ x3e−x2 dx ;
	0
5)	+∞∫ x 3−3 xdx ;
	1
7)	+∞∫ e− x dx ;
	0
	1		dx
9)	∫0						;
		x2 − 4x + 3
11) ∫1			dx			;
			(x −1)	3
	0
13) ∫2 ln xdx ;
	0
	2
15)	∫π cos 1 dx2 ;
	0		x x

17) ∫0 x е3 хdx ;

−∞

	2)	+∞∫	ln3 xdx ;
		1	x
		+∞	dx
	4)	∫0		;
			1 + x3

0x

6)∫ x 23 dx ;

−∞

8)	+∞∫ xsin 2xdx ;
	1
	2
10)	e∫				ln x	dx ;
	1				x
	2				dx
12)	∫0						;
				x2 + x
14)	∫1				dx			;
				3	x +
	0						x

16) π∫tgxdx ;

0

18) ∫0 еx sin xdx ;

−∞

121

19) ∫1 sin	π	dx3 ;
	2
0	x	x

π 2

20) ∫ctgxdx .

0

ТЕМА 5

ГЕОМЕТРИЧЕСКОЕ ПРИЛОЖЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

Вычисление площадей в декартовой системе координат

Площадь S криволинейной трапеции, ограниченной сверху графиком функции y = f (x) , снизу осью Ox , слева и справа соответственно прямыми

x = a и x = b (рис. 6.1), вычисляется по формуле

b

S = ∫ f (x) dx .

a

Для трапеции, лежащей под осью Ox (рис. 6.2), площадь S вычисляется

по формуле
S = ∫b		f (x)		dx = −∫b	f (x)dx .	(6.18)
a				a
у					у
y = f (x)					а	b x
		S			S
					y = f (x)
а				b	x
Рис. 6.1					Рис. 6.2

Первое равенство в (6.18) справедлива и в случае, когда функция y = f (x) на отрезке [a,b] конечное число раз меняет знак.

у

y = f2 (x)

S

y= f1 (x)

аb x

122

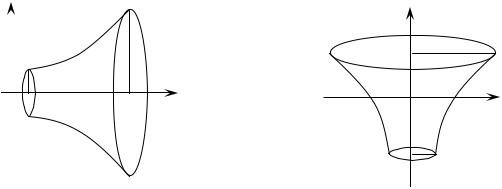
Рис. 6.3

Если криволинейная трапеция ограничена прямыми x = a и графиками

кривых y = f1(x) и y = f2 (x) , причем	f2 (x) ≥ f1(x) , то ее площадь (рис. 6.3) равна
S = ∫b [f2 (x) − f1(x)]dx .	(6.19)
a
Заметим, что формула (6.19)	справедлива для любых функций f1(x) и

f2 (x) – как положительных, так и отрицательных; единственное требование –

f2 (x) ≥ f1(x) .

Если криволинейная трапеция ограничена справа графиком функции x = g( y) , слева осью Oy , снизу и сверху прямыми y = c и y = d , то ее площадь

вычисляется по формуле

S = ∫d g( y)dy .

c

Вычисление объема тела вращения

Объем Vx тела, образованного вращением вокруг оси Ox криволинейной трапеции, ограниченной кривой y = f (x) ( f (x) ≥ 0 ), осью абсцисс и прямыми x = a и x = b ( a < b ) (рис. 6.4), выражается интегралом

Vx =π ∫b	f 2 (x)dx .	(6.20)
a
Аналогично, объем Vy тела, образованного вращением вокруг оси Oy
криволинейной трапеции, ограниченной кривой x = g( y)		( g( y) ≥ 0), осью орди-
нат и прямыми y = c и y = d ( c < d ) (рис. 6.5), выражается интегралом
Vy =π∫d g2 ( y)dy .		(6.21)
c
у		у
y = f (x)
		d
a	b x

x x = g( y)

c

123

Рис. 6.4.

Рис. 6.5.

Вычисление длины дуги плоской линии, заданной в декартовой системе координат

Если плоская кривая задана уравнением y = f (x) и ее производная f ′(x) непрерывна, то длина дуги этой кривой определяется формулой

l = ∫b	1 +[f ′(x)]2 dx .	(6.22)
a

Примеры решения задач

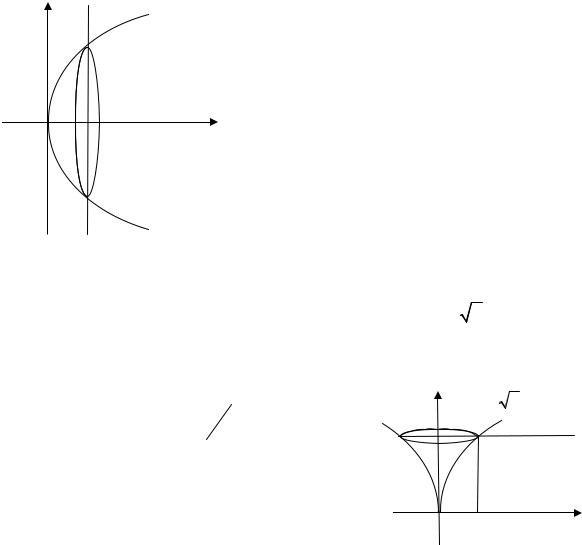
Пример 6.50. Вычислить площадь фигуры, ограниченной графиками

функций y = 4 − x2	и y = x2 −2x (рис. 6.6).
Решение. Найдем абсциссы точек A и B пересечения данных парабол:
4 − x2 = x2 −2x x2 − x −2 = 0 x = −1, x =2 .
	1	2
у	y = 4 − x2	у
			−2 y2
А	y = x2 −2x	x =1
		x = −y2
	В		x
−1	2 x
	Рис. 6.6	Рис. 6.7

Для вычисления площади полученной фигуры используем формулу (6.19):

2																2
S = ∫						2	) −(x			2						= ∫(−2x		2	+ 2x + 4)dx =
	(4 − x										− 2x) dx
−1																−1
		2	x	3	+ x			2					2	= −	16	+ 4	+8 −			2		(кв. ед.).
= −		3							+ 4x						3					3	+1− 4 = 9
													−1
Пример 6.51. Вычислить площадь фигуры, ограниченной параболами
x = −y2 и x =1−2 y2		(рис. 6.7).

Решение. Находим ординаты точек пересечения заданных кривых:

124

−y2 =1−2 y2 y2 =1 y = −1, y

2

=1.

1

Тогда искомая площадь равна

1

2

2

1

2

y

3

1

S = ∫

)

−(−y

= 2∫

(−y

+1)dy = 2

−

+ y

=

(1 − 2 y

) dy

3

−1

0

0

1

1

4

= 2

−

+

=

(кв. ед.).

3

1

3

0

Пример

6.52.

Вычислить

площадь

фигуры, ограниченной линиями

y = 4 − x2 и y = 0 .

Решение. Находим точки пересечения данной параболы и оси Ox ( y = 0 ):

4 − x2 = 0 x = −2, x = 2

. Тогда

1

2

2

2

x3

2

8

8

32

S = ∫(4 − x

)dx =

4x

−

= 8 −

− −8 +

=

(кв. ед.).

3

3

3

−2

−2

3

у

Пример 6.53. Определить объем

тела, образованного вращением вокруг

y2

= 4x

оси Ox фигуры, ограниченной линия-

ми y2 = 4x ( y ≥ 0 ) и x = 2 .

Решение. В прямоугольной сис-

0

2

x

теме координат строим фигуру, огра-

ниченную данными линиями (рис. 6.8).

По формуле (6.20) находим объем:

V =π ∫2

2

4xdx =π 2x2

=8π (куб. ед.).

0

0

Рис. 6.8

Пример 6.54. Фигура,

ограниченная дугой кривой y = 2

x ,

осью Oy и

прямой y = 2 , вращается вокруг оси Oy . Вычислить объем полученного тела вращения (рис. 6.9).

Решение.	По условию y [0;2], следова-			у	y = 2	x
		y2
тельно, обратная функция x =			4 рассматрива-	2
ется на отрезке	x [0;1] . Тогда,		используя фор-
мулу (6.21), находим искомый объем:
				0	1	x

125

	2		y	2		2			π	2		π			2		2π
V =π	∫0						dy =			∫0	y4dy =		y5			=		(куб. ед.).
			4					16				80					5
															0			Рис. 6.9

Пример 6.55. Вычислить длину дуги параболы y = 23 x32 , если x [0;3].

Решение. Так как y′ = x , то по формуле (6.22) получаем

3	1 + xdx =	2	3		3	2	(2	43	− 2 13 )=	14	(ед.).
l = ∫			(1 + x)2		=
0		3			0	3				3

Задания для самостоятельного решения

6.25. Найти площадь фигуры, ограниченной линиями:

		1)			y =3 − 2x − x2 , y = 0 ;			2) y2 =5x, x =1;
		3)			xy = 4, x =1, x = 4, y = 0 ;		4)	y = ln x, x = e, y = 0 ;
		5)			y = x3 , y =8, x = 0 ;		6)	y = x2 +3x, y = x +3 ;
		7)			y = x2 , x =3, x =6, y =0 ;		8)	y2 = 2x +1, y = x −1;
		9)			y2 =16 −8x,	y2 = 24x + 48;	10)	y = x2 −4x,	y = x −4 ;
		11)			y = 3 , y = 4ex , y = 3, y = 4 ;		12)	y = 4 − x4 ,	y = 3 x ;
					x	x2 = −6 y, ( y ≤ 0) ;	14)	y = x2 , y = 2 − x2 .
		13) x2 + y2 = 72,
		6.26. Вычислить				внутреннюю площадь,	ограниченную		эллипсом
x2	+	y2		=1.
a2		b2

6.27.Окружность x2 + y2 = 4 разделена параболой y2 =3x на две части. Найти площадь обеих частей.

6.28.Найти площади фигур, на которые парабола y2 = 2x делит окруж-

ность x2 + y2 =15.
6.29. Вычислить		площадь	фигуры,	ограниченной	линиями	y =sin x ,
y = cos x , x = 0 , x =π	4	.
						y = sinπx ,
6.30. Вычислить		площадь	фигуры,	ограниченной	линиями,
x = −0,5 , x =1,5 .
6.31. Вычислить		площадь	фигуры,	заключенной	между	параболой

y = x2 −4x +3 и касательными, проведенными к параболе в точках (3;0) и (0;3) . 6.32. Вычислить площадь фигуры, ограниченной кривыми y = ln x и

y = ln2 x .

126

6.33.Найти площадь поверхности, образованной вращением вокруг оси Ox дуги кривой y = e−2 x , если.

6.34.Найти площадь, заключенную между кривой y = e−x ( x >0 ) и осями

координат.

6.35. Найти площадь фигуры, ограниченной кривыми y = ln(x + 2) , y = 2ln x , y = 0 .

6.36.Вычислить объем тела, образованного вращением фигуры, ограниченной линиями y = ex , x = 0, x =1, y = 0 вокруг оси Ox .

6.37.Вычислить объем тела, образованного вращением фигуры, ограниченной линиями y =5x − x2 , y = 0 , вокруг оси Ox .

6.38.Вычислить объем тела, образованного вращением вокруг оси Ox

фигуры, ограниченной параболами y = x2 , y = x .
		6.39. Вычислить объем тела,			образованного вращением линии y =			x
						1		+ x2
вокруг оси Ox .
		6.40. Вычислить объемы тел, образованных в результате вращения эллип-
са	x2	+	y2	=1 вокруг:
	a2		b2
		1) оси Ox ; 2) оси Oy .
		6.41. Вычислить объем тела,			образованного вращением вокруг оси			Oy

фигуры, ограниченной линиями y = x2 , x =3, y =1.

6.42.Вычислить объем тела, образованного вращением вокруг оси Oy фигуры, ограниченной линиями y = ln x, x = 2, y = 0 .

6.43.Вычислить объемы тел, ограниченных поверхностями, образованными при вращении линий y = e−x , x =0, y =0 (x ≤0) :

1) вокруг оси Ox ; 2) вокруг оси Oy .

6.44.Вычислить объем тела, образованного вращением вокруг оси Ox фигуры, ограниченной линиями y = xex , y = 0, x =1.

6.45.Вычислить объем тела, образованного вращением вокруг прямой y =1 фигуры, ограниченной графиком функции y =1 +cos2 x (−π 2 ≤ x ≤π 2).

6.46.Вычислить тела, образованного вращением вокруг оси Oy фигуры,

ограниченной линиями y = x2 2 + 2x + 2 и y = 2 .

6.47.Вычислить длину дуги кривой y = ex , заключенной между точками

A(0;1) и B(1;e) .

6.48.Найти длину окружности x2 + y2 = r2 .

6.49.	Найти длину линии y = ln x от x1 = 3 до x2 =	8 .
6.50.	Найти длину дуги кривой y = ex +6 , если ln	8 ≤ x ≤ ln 15 .

127

3
6.51. Найти длину линии y = x2	, если 0 ≤ x ≤12 ;

6.52. Найти длину линии y = ln(1 − x2 ) , если 0 ≤ x ≤ 0,5

Задание для индивидуальной работы № 14

Задание 14.1. Используя метод непосредственного интегрирования вычислить интегралы (табл. 14.1). Сделать проверку.

Таблица 14.1. Распределение вариантов

Номер

варианта

∫

2

∫

2x

2

x dx

x

x

1

а)

sin(2x +3) +

−

x dx

б)

+

3

∫

3

x

9 − x2 −9 + x2

2

а)

2cos(2 − x) −

+3

dx

б)

dx

sin

2

x

∫ (9 − x2 )

9 − x2

∫

−

x

2

x3

3 2

x

+ 2

3

x

3

а)

e

3 +

+ 4

dx

б)

∫

dx

3x

2x

∫

5

x

3

∫

1

2

4

а)

+ 4 2

−

dx

б)

3 x +

dx

2

x

x2

cos

3 x

3

а) ∫

x

2

б) ∫

3x5

+ 2x2

5

5

+

dx

x

dx

1 − x

2

∫

2

+ 7x

4x

5

+

3x

3

+

x dx

6

а)

3cos(5 − 2x) +

dx

б)

∫

x2

3

x2

∫

5

−

∫

1

2

7

а)

3 3x −

2 +

−e

2 x

dx

б)

−

4 + x2

dx

3x

4 + x2

а) ∫

5

7

б) ∫3x

4

+

2х

2

+

3

x

2

8

cos3x +

−

dx

dx

5

x

2

1

+

4x

2

x

∫

2

2

∫

3x5

+ х3 + х

9

а)

3x

+5 +

dx

б)

dx

3x

x

3

∫

x

5

x

4

+3 +

5

x

2

10

а)

2 +3 x −

dx

б)

∫

dx

1 −

9х

2

x2

∫

3

−3−

х + 3 2х+

∫

5x

5

+

3х

3

+ 2 dx

11

а)

5

dx

б)

x

9 − x2

∫

8

3

∫

2х

+3

1

12

а)

sin(πx) +

+

dx

б)

x

−

dx

3

x

x2 −

4

3

cos

2

(3

− x)

128