Практикум по высшей математике_часть 2

Подчеркнем, что условие (8.3) только необходимое условие сходимости ряда, т.е. условие, при нарушении которого ряд не может сходиться. С помощью этого признака можно доказывать только расходимость ряда.

В дальнейшем будут рассматриваться числовые ряды a1 + a2 +... + an +... , все члены которых положительны.

Критерий сходимости числового ряда. Достаточные признаки сходимости числового ряда

Для того чтобы ряд (8.1) с положительными членами сходился, необходимо и достаточно, чтобы последовательность его частичных сумм (8.2) была ограничена.

Указанный критерий имеет, скорее, теоретическое, нежели практическое значение. Поэтому необходимо уметь использовать достаточные признаки сходимости ряда: радикальный и интегральный признаки Коши, признак сравнения, признак Д’Аламбера.

Радикальный признак Коши. Если для ряда (8.1) с положительными членами существует предел

lim n an = K ,

n→∞

то при K <1 ряд сходится, при K >1 – расходится, при K =1 вопрос о сходимости ряда остается открытым.

Интегральный признак Коши. Пусть задан ряд

∞
f (1) + f (2) +... + f (n) +... = ∑ f (n) ,	(8.4)

n=1

члены которого являются значениями непрерывной, положительной и монотонно убывающей функции f (x) при x ≥1. Тогда ряд (8.4) будет сходящимся,

если будет сходящимся несобственный интеграл ∞∫ f (x)dx , т.е. ∞∫ f (x)dx = A <∞ ,

1

1

и расходящимся, если этот интеграл будет расходящимся, т.е. ∞∫ f (x)dx = ∞ или

1

не существует.

Признак сравнения. Пусть даны два ряда с положительными членами:

a1 + a2 +... + an +... ,	(8.6)
b1 +b2 +... +bn +...,	(8.7)

причем члены первого ряда не превосходят соответствующих членов второго, т.е. an ≤ bn (n =1,2,...). Тогда из сходимости ряда (8.7) следует сходимость ряда

178

(8.6). Из расходимости меньшего ряда (8.6) следует расходимость большего ря-

да (8.7).

Замечание 1. Признак сравнения можно использовать и в том случае, когда неравенство an ≤ bn выполняется не для всех членов рядов (8.6) и (8.7), а на-

чиная с некоторого номера N .

Замечание 2. При исследовании рядов с помощью признака сравнения нужно знать, какие ряды сходящиеся и какие расходящиеся. Для сравнения удобно пользоваться рядами:

∞

cxoдится, если

q

<1,

1)

∑bqn−1

q

n=1

pacxoдится, если

≥1;

∞

1

cxoдится, еслиα>1,

2)

∑

α

n=1

n

pacxoдится, еслиα ≤1.

Предельный признак сравнения. Если

0 < lim an <∞,

n→∞ bn

то ряды (8.6) и (8.7) либо оба сходятся, либо оба расходятся.

Признак Д’Аламбера. Если для ряда с положительными членами a1 + a2 +... + an +... существует предел

lim an+1		= D ,	(8.8)
n→∞	a
	n

то ряд сходится в случае D <1, расходится в случае D >1 и нуждается в дополнительном исследовании при D =1.

Знакопеременные ряды. Признаки сходимости знакопеременных рядов

Ранее мы рассматривали только ряды с положительными членами. Рассмотрим теперь ряды с членами произвольного знака, или, как принято гово-

рить, знакопеременные ряды.

Особенно часто среди знакопеременных рядов встречаются ряды, члены которых имеют чередующиеся знаки, т.е. знакочередующиеся ряды.

Условимся считать первый член ряда положительным. Тогда знакочередующийся ряд в общем виде запишется так:

a − a	+ a − a	4	+... + (−1)n−1 a	n	+...	(8.9)
1 2	3

где все an (n =1,2,...) положительны.

179

Для проверки сходимости знакочередующегося ряда используют признак Лейбница.

Признак Лейбница. Если члены знакочередующегося ряда (8.9) удовлетворяют условиям:

1) убывают по абсолютной величине, т.е. a1 > a2 > a3 >... ;

2) lim an = 0 ,

n→∞

то ряд (8.9) сходится и его сумма не превосходит первого члена.

Ряд называется знакопеременным, если он содержит бесконечное число как отрицательных, так и положительных членов. Рассмотрим такой ряд:

a1 + a2 +...

+ an +... .

(8.10)

Составим ряд из абсолютных значений ряда (8.10):

a1

+

a2

+

+

an

+

(8.11)

Если ряд (8.11), составленный из модулей, сходится, то сходится и ряд

(8.10). При этом ряд (8.10) называют абсолютно сходящимся рядом.

Заметим, что ряд (8.10) может сходится, а ряд (8.11), составленный из модулей, при этом расходится. В этом случае ряд (8.10) называется условно схо-

дящимся рядом.

Примеры решения задач

Пример 8.1. Исследовать сходимость ряда

∞

b +bq +bq2 +... +bqn−1 +... = ∑bqn−1 .

n=1

Если в качестве последовательности {an , n =1,2,3,...}

(8.12)

рассмотрена беско-

нечная геометрическая прогрессия с первым членом b ≠ 0 и знаменателем q . Решение. При q <1 ряд (8.12) является сходящимся, как убывающая гео-

метрическая прогрессия, и его сумма равна S = 1 −b q . Например,

		1		1		1	∞		1 n−1			1
1	+		+		+		... = ∑			=				= 2 .
		2		4		8							1
							n=1		2	1		−
													2

Пример 8.2. Исследовать сходимость ряда

112 + 213 +... + n(n1+1) +... .

180

Решение. Так как

	1	=	1	−	1		,
	n(n +1)		n		n +1

то для n -ой частичной суммы ряда получаем выражение

		1 1			1			1		1
Sn = 1	−		+	−	3		+... +		−		.
		2	2				n			n +1

После раскрытия скобок все слагаемые, кроме первого и последнего, взаимно уничтожаются, и в результате получаем

Sn =1 − n 1+1 .

Отсюда следует, что lim Sn =1. Итак, ряд сходится и его сумма равна 1.

n→∞

Пример 8.3. Исследовать на сходимость ряд

12 + 23 +... + n n+1 +....

Решение. Имеем

lim a	n	= lim	n		=1 ≠ 0 ,
n→∞		n→∞ n +1

т.е. необходимый признак (8.3) сходимости ряда не выполняется, поэтому данный ряд расходится.

Пример 8.4. Исследовать сходимость ряда

1 + 12 + 13 + 14 +... + 1n +... .

Решение. Данный ряд называется гармоническим рядом. Очевидно, что для гармонического ряда выполнено необходимое условие сходимости, так как

lim a	n	= lim 1	= 0 .
n→∞		n→∞ n

Тем не менее, в примере 8.6 будет показано, что гармонический ряд является расходящимся. Рассчитаем пока несколько его частичных сумм:

S10 = 2,929; S100 = 5,187; S1000 = 7,485; S10000 = 9,788 .

Видно, что частичные суммы растут медленно, не стремясь к какому-то конкретному пределу S .

181

Пример 8.5. Исследовать сходимость ряда ∑∞ 4n n . n=1 n +1

Решение. Для исследования применим радикальный признак Коши. По условию an = n4+n1 n и

lim n an = lim n4+n1 = 4 >1.

n→∞ n→∞

Так как предельное значение больше единицы, то исследуемый ряд расходится.

Пример 8.6. Выяснить, при каких значениях α (α > 0) сходится ряд

1 +

1

+

1

+... +

1

+... .

(8.13)

α

α

α

2

3

n

Решение. Рассмотрим функцию

f (x) =

1

(x ≥1).

xα

Данная

функция

монотонно убывает, поскольку

ее производная

f / (x) = −

α

при α > 0

и x ≥1 отрицательна. Поэтому, согласно интегрально-

xα+1

му признаку Коши, сходимость ряда (8.13) эквивалентна сходимости несобст-

∞

dxxα . Заметим (см. пример 6.49), что

венного интеграла ∫1

1

∞

,

α ≠1;

(1

−

α)x

α−1

1

∞

dx

∫

=

x

α

1

∞,

ln

x

α =1.

1

Следовательно, интеграл сходится при α >1 и расходится при 0 <α ≤1. Значит, и ряд (8.13) сходится при α >1 и расходится при α ≤1. Так как при α =1 ряд (8.13) становится гармоническим

1 + 12 + 13 + 14 +... + 1n +... ,

то, согласно интегральному признаку Коши, он является расходящимся рядом.

182

					∞	1
	Пример 8.7. Исследовать сходимость ряда ∑						.
						n
					n=1	n 3
	Решение. Так как
		1	≤	1	, n =1,2,...,
		n		n
		n 3		3

∞
и ряд ∑ 1n является сходящимся как геометрическая прогрессия со знаменате-
n=1	3

лем q = 13 <1, то, согласно признаку сравнения, исследуемый ряд тоже является сходящимся.

Пример 8.8. Исследовать сходимость ряда 12 + 222 + 233 +... + 2nn +... .

Решение. Сходимость ряда исследуем с помощью признака Д’Аламбера. Для того чтобы применить этот признак, рассчитаем предел вида (8.8):

lim an+1

n→∞ an

n +1 n

n +1

2n

= lim

n+1

:

= lim

n+1

2

2

n

2

n

n→∞

n→∞

1

n +1

=

1

1

=

= lim

2

lim 1 +

n→∞

n

2 n→∞

n

=

12 <1.

Следовательно, исходный ряд является сходящимся. Пример 8.9. Исследовать сходимость ряда

1 − 212 + 312 − 412 +... + (−n1)2n−1 +... .

Решение. Данный числовой ряд является знакочередующимся. Для иссле-

дования его на сходимость используем признак Лейбница. По условию an = n12 .

Тогда

1) 1 > 212 > 312 > 412 >...;

2) lim 12 = 0 .

n→∞ n

Выполняются оба условия из признака Лейбница, следовательно, ряд сходится. При этом ряд, составленный из абсолютных величин

183

1 + 212 + 312 + 412 +... + n12 +...

так же сходится как обобщенный гармонический ряд с α =2 >1. Значит, исходный ряд сходится абсолютно.

Пример 8.10. Показать, что ряд ∑∞ (−1)n сходится условно.

n=1 n

Решение. Данный ряд – знакочередующийся. Так как an = 1n и

1) 1 > 12 > 13 > 14 >...;

2) lim 1 = 0 ,

n→∞ n

то по признаку Лейбница ряд сходится.

С другой стороны ряд, составленный из модулей

∞		=1 +	1		1	+....
∑1				+
n=1	n		2		3

является гармоническим и, значит (см. пример 8.6), расходится. Следовательно, исходный ряд сходится условно.

Задания для самостоятельного решения

8.1.Проверить, выполняется ли необходимое условие сходимости ряда:

1) 12 + 34 + 56 + 78 +...;

3) 11 + 13 + 15 + 17 +... ; 5) 1 + 12 + 14 + 18 +...;

7)	1	1	2	2		3 3
			+		+		+... ;
	2		3			4
9)	∞	2n +1 ;
	∑
	n=1	n + 2

2) 1+ 12 + 13 + 12 +...; 4) 23 + 94 + 276 + 818 +...;

6) 2 +3 + 4 +5 +...;

8) 12 + 15 +101 +171 +...;

10) ∑∞ 1 . n=1 n(n + 2)

8.2.Используя признаки Коши, исследовать на сходимость ряды:

	1)	1	+	1	+	1	+	1	+... ;	2) 1 +	1	+	1	+	1	+...;
		3		5		7		9			4		7		10

184

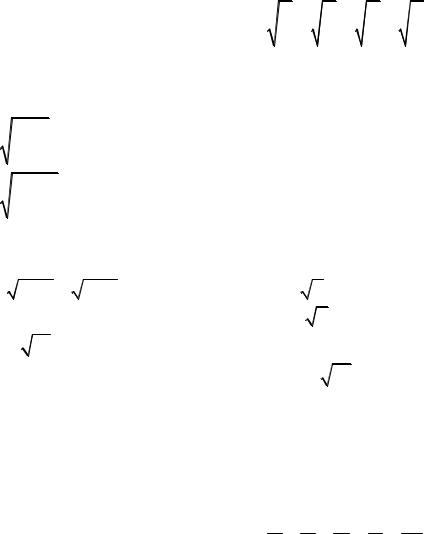
3)		1			+							1						+				1				+	...;		4)		1		+				2			+				3	+...;
		ln 2										2			3							3			4						3						3							3
										ln												ln								2						3								4
5)		1						+								2						+				3		+... ;	6)			1							+					1				+	1		+... ;
					2							1								2						2						2				2								2			3		2	4
	1 +1													+ 2									1 +3									2ln											3ln						4ln
		∞									π																					∞				1
7)	∑sinn															;													8)	∑												;
																																									2
		n=1									3n																					n=1 1 + n
		∞						1																								∞					n		n + 2
9)	∑																			;									10) ∑ln																			;
												2		−1																														+3
		n=1 (2n)																														n=1							n
		∞			1 n +1 n2																											∞									n
11) ∑																							;						12) ∑																		.
				5		n																															n		(n +1)
		n=1								n					−1																	n=1 ln

8.3.Используя признак сравнения, исследовать на сходимость ряды:

1)	1 +		1		+			1				+			1			+...;	2)	1	+	1	+	1		+	1		+...;
			2 5			3		5			2						3
															4 5					ln 2 ln 3 ln 4						ln 5
3)		1		+		1				+				1			+...;		4)	2	+	2	+	2	+		2	+...;
	2 +1				4 + 2							8		+3						1		2		3			4

5) 10 +5 +10

+10

+...;

6)

2

+

2

+

2

+...;

5

25

125

3

4

1

∞

n +2 1

∞

n −

7) ∑

;

8) ∑

2

;

n

3

n=1

n

n=1

∞

2

∞

2n

9) ∑3

;

10)

∑

;

2n −

1

2

n=1

n=1

2n −1

∞

1

∞

1

11) ∑ln 1 +

;

12)

∑

;

n

ln(n +1)

n=1

n=1

∞

n +1 −

n −1

∞

5

n +3

13) ∑

;

14)

∑

;

n

n n − 4

n=1

n=1

∞

4

n

3

∞

2

(n + 2) .

15) ∑

;

16)

∑ln

ln(n +1)

n=1

n=1

n 5 n4

8.4.Используя признак Д’Аламбера, исследовать на сходимость ряды:

	1)	1 +		3		+			5		+		7			+...;
				9				27
		3									81
	3) 1 +			3				+			32				+		33				+... ;
			2 3							22 5							23		7
	5)	1 +		1		+		1		+		1			+			1		+... ;
				2				6									120
		1									24
		∞		2	n−1
	7)	∑						;
		n=1		n!

2) 1 +11 23 +11 32 53 +... ;

4)12 + 24 + 86 + 1624 +12032 +...;

6)3!1 + 5!1 + 7!1 + 9!1 +11!1 +...

8)∑∞ nnn! ;n=1

185

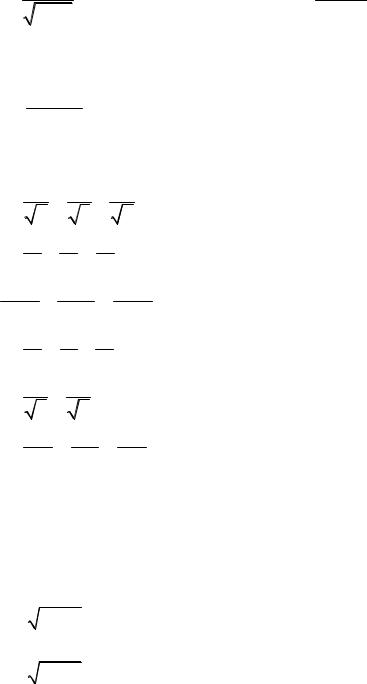
9) ∑∞ 4n −3 ;

n=1 n 3n

∑∞ n3 −3

11) n=1 3n+1 ;

∞52n+1

13)∑n=1 (n + 2)!;

∞32n−1

10)∑n=1 (n +1)! ;

12)	∞	(2nn		+1)!		;
	∑
	n=1	4		n!
	∞	2	n
14)	∑				.
		(n!)		2
	n=1

8.5. Установить какие ряды сходятся абсолютно, условно или расходятся: 1) 1 − 12 + 13 − 14 +...;

2)1 − 312 + 512 − 712 +...;

3)2ln1 2 − 3ln1 3 + 4ln1 4 −...;

4)1 − 213 + 313 − 413 +...;

5)1 − 13 + 15 −... ;

6)1 − 21a2 + 31a4 − 41a6 +... ;

∞

n−1

∞

n−1

7) ∑(−1)

3 ;

8) ∑(−1)

;

n=1 (4n)

n=1

n!

∞

n

∞

(−1)

n

9)

∑cos52

;

10)

∑

;

2

n

n=1

n

n=1

nln

∞

(−1)

n+1

∞

11)

∑

;

12)

∑tg (2n −1)π

;

=

n

2

+1

=

4

n 1

n 1

∞

(−1)

n+1

∞

12)

∑

;

13)

∑sin25n

;

n3 +

1

n=1

n

n=1

n

14)

∞

n−1 n +1

15)

∞

(−1)n+15n

∑(−1)

;

∑

n ;

n=1

n

n=1

(n +1)3

∞

n+1

∞

n

n

16)

∑(−3)n

;

17)

∑

(−1)

4

.

n=1

4

n=1

(n +1)!

186

ТЕМА 2

СТЕПЕННЫЕ РЯДЫ

Степенным рядом называется ряд вида

					∞
a0	+ a1x + a2 x2 +... + an xn +... = ∑an xn ,						(8.14)
					n=0
или ряд более общего вида
a	+ a (x − x ) + a (x − x )2				+... + a (x − x )n +... =
0	1	0	2	0	n	0
						∞
						= ∑an (x − x0 )n ,	(8.15)

n=0

где x0 – постоянная величина, a0 , a1, a2 ,..., an ,... – некоторая числовая последовательность. Постоянные a0 , a1, a2 ,..., an ,... называются коэффициентами степен-

ного ряда. О ряде (8.14) говорят, что он расположен по степеням x , о ряде (8.15) – что он расположен по степеням двучлена.

Так как замена x − x0 =t сводит ряд (8.15) к ряду (8.14), то в дальнейшем

будем рассматривать степенной ряд вида (8.14).

Придавая переменной x различные числовые значения, получают различные числовые ряды, которые могут сходиться или расходиться. Множество тех значений x , при которых ряд (8.14) сходится, называется областью сходимости степенного ряда. Область сходимости любого степенного ряда не пуста, поскольку очевидно, что ряд (8.14) сходится при x = 0 .

Для степенного ряда (8.14) возможны только три случая:

1) ряд сходится в единственной точке x = 0 ; 2) ряд сходится для всех значений x ;

3) существует такое R > 0 , что ряд сходится для всех значений x из интервала (−R, R), и расходится для всех значений x вне отрезка [−R, R].

Интервал (−R, R) называется интервалом сходимости ряда (8.14), а чис-

ло R – радиусом сходимости этого ряда.

Понятие радиуса сходимости будем распространять на все три указанных случая. При этом в первом случае R = 0 , а во втором – R = ∞.

Радиус сходимости степенного ряда чаще всего находят с помощью признака Д’Аламбера и Коши.

Признак Д’Аламбера. Если существует предел

D = lim an+1 ,

n→∞ an

187