Практикум по высшей математике_часть 2

неопределенного интеграла. Для этого достаточно вычислить производную от правой части равенства, которая должна быть равна подынтегральной функции.

Таблица основных интегралов

1.	∫xα dx =				xα+1				+C	(α ≠ −1) ; ∫dx = x +C ; ∫0 dx =C .
		α +1
2.	∫dx = ln				x		+C.
	x
					ax
3.	∫axdx =							+C (a > 0, a ≠1).
		ln a

4.∫exdx = ex +C.

5.∫sin xdx = −cos x +C.

6.∫cos xdx = sin x +C.

7.∫cosdx2 x = tgx +C.

8.∫sindx2 x = −ctgx +C.

dx

= ln

x

+

π

+C.

9.

tg

∫cos x

2

4

10.∫sindxx = ln tg 2x +C.

11.∫tgxdx = −ln | cos x | +C.

12.∫ctgxdx = ln | sin x | +C.

∫

dx

1

x

1

x

13.

= a arctg

+C = − a arcctg

+C

(a ≠ 0) .

a2 + x2

a

a

14.

∫

dx

= arcsin

x

+C = −arccos

x

+C

(a ≠ 0) .

a

2

2

a

− x

a

∫

dx

1

x − a

+C

(a ≠ 0).

15.

=

ln

x2 − a2

2a

x + a

∫

xdx

1

x

2

+ a

+C

(a ≠ 0).

16.

=

2 ln

x2 + a

∫

dx

17.

= ln

x +

x2 ± а

+C

(a ≠ 0).

2

∫

x

± а

1 x

+ a2

x

18.

a2 − x2 dx =

a2 − x2

arcsin

+C

(a ≠ 0) .

2

(x

2

a

)+ C (a ≠ 0) .

19.

∫

a2 + x2 dx = 12

a2 + x2 + ln

x +

a2 + x2

69

Пример 6.1. Проверить, правильно ли найдены следующие интегралы:

1)

∫5

x

dx =

5x

+C ;

3) ∫

2x +3cos2 x

dx = 2tgx +3ln | x | +C ;

ln x

x cos2 x

2)

∫(х

3

+3)dx

=

1

x

4

+3х+C ;

4) ∫

1 − х2 − х2 + х4

dx = arcsinx −

x3

+C .

4

1 − x

2

3

Решение. 1) Для проверки достаточно вычислить производную от правой части равенства. Для любого значение константы C справедливо равенство

	5	x	′		1	(5x )′ =	1	5x ln 5 = 5x .
			+C	=
					ln 5		ln 5
ln 5

Интеграл найден правильно. 2) Найдем производную:

	1	х	4	′	3	+3 .
	4			+3х+С = х

Так как в результате дифференцирования получено подынтегральное выражение, то интеграл найден верно.

3) Находим производную:

2		3		2x +3cos2 x
(2tgx +3ln | x | +C )′ =		+ x	=	x cos2 x	.
	cos2 x

Интеграл найден верно.

4) Преобразуем подынтегральное выражение:

1

− х2 − х2 + х4

1− х

2

х2 (1−х2 )

1

2

∫

dx =∫

−

dx =∫

− х

dx .

1− x

2

1− x

2

1− x

2

1− x

2

Производная от результата интегрирования равна

	x	3	′		1	− x2 .
arcsinx −			+C	=
	3
					1 − x2

Таким образом, с учетом сделанных выше преобразований, делаем вывод, что интеграл вычислен правильно.

70

Основные свойства неопределенного интеграла

1. Производная от неопределенного интеграла равна подынтегральной функции:

(∫ f (x)dx)′ = (F (x) +C )′ = F′(x) = f (x) .

2.Дифференциал от неопределенного интеграла равен подынтегральному выражению:

d(∫ f (x)dx)= (∫ f (x)dx)′dx = f (x)dx .

3.Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная константа:

∫dF(x) = F (x) +C .

4.Постоянный множитель (не равный нулю) можно выносить из под знака интеграла:

∫α f (x)dx =α∫ f (x)dх.

5.Неопределенный интеграл от алгебраической суммы двух или нескольких функций равен алгебраической сумме интегралов от этих функций

∫( f1(x) ± f2 (x))dx = ∫ f1(x)dx ± ∫ f2 (x)dx .

6.Если F(x) является первообразной для функции f (x) , то

∫f (αx +b)dx = α1 F(αx +b) +С.

Свойство 6 называют теоремой о линейной замене в неопределенном интеграле.

Из свойств 2 и 3 следует, что операции интегрирования и дифференцирования взаимно обратны.

Существуют неопределенные интегралы от элементарных функций, которые не выражаются через элементарные функции, например,

∫e−x2 dx , ∫	sin x	dx ,	∫sin x2dx , ∫ 1 − k 2 sin2 xdx , ∫	x	dx
				ln x
	x

и многие другие. Такие интегралы представляют собой новые функции, которые не выражаются через элементарные функции. Эти интегралы называются «неберущимися».

71

Непосредственное интегрирование

Непосредственное интегрирование заключается в приведении подынтегрального выражения к табличному с помощью элементарных преобразований и свойств неопределенного интеграла.

	∫		5			3
Пример 6.2. Найти I =					− 4x		+ cos3x dx .
			1 + x	2

Решение. Используя свойства 4 и 5 неопределенного интеграла, таблицу интегралов, получаем

∫

5

3

∫

dx

∫

3

∫

I =

− 4x

− 4

x dx +

cos3xdx

1

+ x

2

1

+ x

2

+ cos3x dx = 5

= 5arctgx − x4 + 13 sin 3x +C .

Проверка. Находим производную:

		4		1	′	5			3
	5arctgx − x		+		sin 3x +C =			− 4х		+ cos3x .
				3		1 + х	2

а также

=

Так как полученный результат совпадает с подынтегральной функцией, то вычисление верно.

Пример 6.3. Найти I = ∫(1 + 4x2 )2

dx .

x

(

Решение.

Преобразовав

числитель

подынтегральной функции

+ 4x2

)

2 =1+8x2

+16x4 и, разделив почленно на знаменатель, получаем

1

I = ∫(1 + 4x2 )2

dx = ∫1 dx +8∫xdx +16∫x3dx = ln | x | +4x2 + 4x4 + C .

x

x

Проверка. (ln | x | +4x

2

4

′

1

3

(1 + 4x2 )2

+ 4x

+C )

= x +8x

+16x

=

x

.

Пример 6.4. Найти I = ∫tg2 xdx .

Решение. Используя тригонометрические формулы, находим:

2

sin2 x

1−cos2 x

1

I =

∫

tg

xdx =

∫cos

2

dx =

∫

2

dx =

∫

−1 dx = tgx

− x +C .

x

cos

x

2

x

cos

′

1

2

Проверка. (tgx − x +C ) =

−1 = tg

x .

cos2 x

72

Пример 6.5. Найти I =∫				dx
					.
			4x2 +9
Решение. Данный интеграл приведем к табличному интегралу 13 и ис-
пользуем свойство 6 неопределенного интеграла:
I =∫	dx		1	1		2x	1	2x
		=	2	3 arctg		3	+C = 6 arctg	3	+C .
	(2x)2 +32

Метод подстановки (метод замены переменной) в неопределенном интеграле

Введение новой переменной интегрирования часто дает возможность свести вычисление данного интеграла к вычислению табличного интеграла. Полагая x =ϕ(t) , где ϕ(t) – непрерывно дифференцируемая функция, получаем

′	(6.1)
∫ f (x)dx = ∫ f (ϕ(t)) ϕ (t)dt.
Формулу (6.1) также применяют и в обратном направлении:
′	(6.2)
∫ f (ϕ(t)) ϕ (t)dt = ∫ f (x)dx , где x =ϕ(t) .

Из формулы (6.2) следует, что при интегрировании целесообразно применять не подстановку x =ϕ(t) , а подстановку t = g(x) .

x3

Пример 6.6. Найти I = ∫(x −1)2 dx .

Решение. Пусть x −1 = t , тогда x = t +1. Значит dx = d(t +1) = dt и

∫

(t +1)3

∫

t3

+3t2 +3t +1

∫

3 1

I =

t

2

dt =

t

2

dt =

+

t

+

t

2

t +3

dt =

= 12 t2 +3t +3ln t −1t +С = 12 (х−1)2 +3(х−1)+ 3ln х−1 −

−

1

+С = 3ln

х−1

−

1

+

х2

− x +

1

+3x −3

+С =

х−

1

х−1

2

2

1

х2

= 3ln

х−1

−

+

+ 2x +С .

х−1

2

1

Здесь С1 =C −2,5 .

73

= ∫ sin x

Пример 6.7. Найти I 1 + cos2 x dx .

Решение. Используем метод замены переменной. Пусть t = cos x . Отсюда dt = −sin xdx и

I = ∫1sin+ cosxdx2 x = −∫1+dtt2 = −arctgt +C = −arctg(cos x)+C .

Пример 6.8. Найти I = ∫cos x x dx .

Решение. Используем метод замены переменной:

				dx
I = ∫cos x	dx =	x = t,				= dt	= ∫cost
			2		x				2tdt =
x		dx = 2	xdt, dx = 2tdt					t
= 2∫costdt = 2sin t +C = 2sin					x +C .

Введение переменной под знак дифференциала

′
Так как ϕ (t)dt = dϕ(t) , то из формулы (6.2) замены переменной и свойств
неопределенного интеграла получаем
					′	∫ f (ϕ(t))dϕ(t) = F(ϕ(t)) +C ,
∫ f (ϕ(t)) ϕ (t)dt =
где ∫ f (u)du = F(u) +C .
В частности справедливы формулы:
		n			′		n		f n+1 (x)
∫ f			(x) f		(x)dx = ∫ f			(x)df (x) =		+C ;
									n +1
∫	f ′(x)			dx = ∫df (x)		= ln | f (x) | +C .
	f (x)				f (x)

Пример 6.9. Найти I = ∫sin3 xcos dx .
Решение.
I = ∫sin3 x(cos dx)= ∫sin3 xd sin x = sin4 x	+C .
4
Пример 6.10. Найти I = ∫xex2 dx .
Решение.

74

t2 − 4

x + x2

∫

x2

∫

x2

1

2

1

∫

x2

2

ex2

I =

e xdx =

e

2

dx

=

2

e

dx =

2

+ C .

Пример 6.11. Найти I = ∫1x++2xx2 dx .

Решение.

I = ∫1x++2xx2 dx = ∫d (x + x2 )= ln | x + x2 | +C .

Простейшие интегралы, содержащие квадратный трехчлен

Интегралы вида

∫	(Ax + B)dx	,	∫	(Ax + B)dx
	ax2 +bx + c			ax2 +bx + c

сводятся к табличным с помощью подстановки x + 2ba = t .

Пример 6.12. Найти интегралы:

1)	I =			dx	;	2) I	2	=	(x −1)dx		.
	1	∫x2		+ 4x +5				∫x2		+ 6x + 7

Решение. 1) Выделяем полный квадрат в знаменателе и вводим новую переменную

I =

dx

=

dx

=

x + 2 =t

=

dt

=

1

∫x2

+ 4x +5

∫(x + 2)2 +1

dx = dt

∫t2 +1

=arctgt +C = arctg(x + 2) +C .

2)Как и в предыдущем примере, выделяем полный квадрат и используем новую переменную

2 = ∫

(x −1)dx

= ∫

(x −1)dx

x +3 = t

= ∫

(t −

I

x

= t −3

=

x2 + 6x +5

(x +3)2 − 4

dx = dt

tdt

dt

1

d (t2 − 4)

t − 2

= ∫

− 4∫

=

2 ∫

t2 − 4

−ln

t + 2

=

t2 − 4

t2 − 4

=

1 ln

t2 − 2

−ln

t − 2

+C = 1 ln

x2 + 6x +5

−ln

2

t + 2

2

4)dt =

x +1 +C = x +5

75

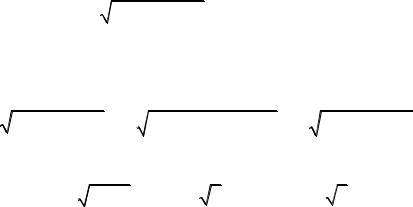
=	1 ln		(x +5)3		+C .
	2		x +1
Пример 6.13. Найти I = ∫								dx	.
						−x	2	+ 2x +5

Решение. Как и в предыдущем примере 6.12, выделяем полный квадрат и делаем замену переменной:

I = ∫

dx

=

∫

dx

=

∫

dx

=

−x

2

+ 2x +

5

−(x

2

−(x −1)

2

+

6

− 2x +1) + 6

=

x −1 = t

= ∫

dt

= arcsin

t

+C = arcsin

x −1

+C .

dx = dt

6 −t

2

6

6

Пример 6.14. Найти I = ∫

(2x −1)dx

.

4x2 + 4x +5

Решение.

I = ∫

(2x −1)dx

= ∫

(2x −1)dx

= ∫

(2x −1)dx

=

4x2 + 4x +5

2

+ 2

1

x

+

5

+

1

2

4 x

2

4 x

2

+1

4

x

+

1

= t

2

1

(2t − 2)dt

1

2tdt

1

dt

=

dx = dt

= 4

∫

t2 +1

=

4 ∫

−

2 ∫

=

t2 +1

t2 +1

2x −1 = 2t − 2

d (t2 +1)

dt

1

1

1

2

1

=

4

∫

t2 +1

−

2 ∫

=

4 ln | t

+1| − 2 arctgt + С =

t2 +1

=

1

ln(4x

2

+ 4x +5) −

1

1

+C .

4

2

arctg x +

2

Интегрирование по частям

Если u(x) и v(x) – дифференцируемые функции, то справедлива формула интегрирования по частям

∫u(x)v′(x)dx = u(x)v(x) − ∫v(x)u′(x)dx .

(6.3)

76

Так как u′(x)dx = du и v′(x)dx = dv , то формулу (6.3) можно переписать в

виде

∫udv =uv − ∫vdu .

Формула интегрирования по частям позволяет свести вычисление интеграла ∫udv к вычислению интеграла вида ∫vdu .

Формула интегрирования по частям применяется для вычисления, например, интегралов, подынтегральная функция которых представляет собой произведение функций разного класса, т.е.

∫xn cos axdx, ∫xn ln axdx, ∫xneaxdx, ∫eax sin bxdx и др.

При этом за u(x) принимается функция, которая упрощается при диффе-

ренцировании. За dv принимается та часть подынтегрального выражения, которая содержит dx и интеграл от которой может быть легко вычислен. За u(x)

обычно обозначают функции ln x, arcsin x, arccos x, arctgx, arcctgx или xn .

Иногда формулу интегрирования по частям приходится использовать несколько раз.

Пример 6.15. Найти I = ∫xexdx .

Решение.

	I = ∫xu	exdx	=		u = x,	du = dx,		=
					dv = exdx,	∫dv = ∫exdx, v = ex
		dv

= xu evx − ∫evx dxdu = xe x − ex +C = e x (x −1)+C .

Пример 6.16. Найти I = ∫xln xdx .

Решение.

u = ln x,

du = dx

,

I = ∫ln x xdx =

x

dv = xdx,

∫dv = ∫xdxv, v = x

2

u dv

2

=

x2

ln x − 1

∫xdx =

x2

ln x −

x2

+C .

2

2

2

4

Пример 6.17. Найти I = ∫arccosxdx .

Решение.

	=	x2	ln x − ∫	x2	dx		=
		2		2
			u			x
		v		v		du

77

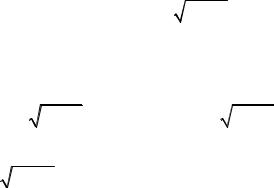
I =

∫

arccos x dx =

u = arccos x,

du = −

dx

=

1 − x

2

u

dv

dv = dx,

v = x

dx

1

d 1 − x2

= xarсcos x +∫x

= xarcсosx −

∫

(

)

=

1 − x

2

2

1 − x

2

v

u

v

−du

= x arccos x −

1 − x2 +C .

Пример 6.18. Найти I = ∫x2 sin xdx .

Решение. С помощью двукратного интегрирования по частям, получаем

I = ∫x2 sin xdx =	u = x2 ,	du = 2xdx			= −x2 cos x + 2∫xcos xdx =
	dv = sin xdx, v = −cos x
= −x2 cos x + 2∫xcos xdx = −x2 cos x + 2					u = x,	du = dx		=
					dv = cos xdx,	v = sin x

= −x2 cos x + 2(xsin x − ∫sin xdx)= −x2 cos x + 2xsin x +

+2cos x +С = (2 − x2 )cos x + 2xsin x +С.

Пример 6.19. Найти I = ∫ex cos xdx .

Решение. С помощью двукратного интегрирования по частям, получаем

I = ∫ex cos xdx =	u = ex ,	du = exdx			=
	dv = cos xdx,	v = sin x
= ex sin x − ∫ex sin xdx = ex sin x −				u = ex ,	du = exdx		=
				dv = sin xdx, v = −cos x
= ex sin x + ex cos x − ∫ex cos xdx +C .
Таким образом, получено равенство
∫ex cos xdx = ex (sin x + cos x)− ∫ex cos xdx +C .

Отсюда, перенеся интеграл из правой части равенства в левую, находим

2∫ex cos xdx = ex (sin x + cos x)+C

78