Практикум по высшей математике_часть 2

27	2∫cos5xcos13xdx		∫		sin2 xdx
					(1 + cos x +sin x)		2
28	∫	sin13xsin 3xdx			(1 +sin 2x)dx
			∫1 + cos 2x +sin 2x
29	∫sin11xcos5xdx		∫		sin xdx
					(1 + cos x +sin x)2
30	∫	5cos 4xcos3xdx			sin 3xdx
			∫2 +sin 3x

Задание для индивидуальной работы № 15

Задание 15.1. Вычислить определенные интегралы (табл. 15.1):

Таблица 15.1. Распределение вариантов

Номер

варианта

1

e2

ln x dx

π∫xsin2xdx

∫1

x

0

2

2x dx

1

2

∫

∫arcsinxdx

x

1 1−4

0

3

∫2

3 1 + x2 xdx

∫e

3 x ln xdx

0

1

4

∫1

x2dx

∫2 (1− x)sinπxdx

6

0

x + 4

−2

5

∫1

exdx

;

∫1

xarctgxdx

2 x

0 1 + e

0

6

e∫ ln x dx

∫2 (3 − 2x)e−3xdx

2

e

x

0

π

sin xdx

π

x

7

∫

∫e

sin xdx

2

x

π 2 1 + cos

0

8

∫e

dx

∫3

x2 ln xdx

x(1+ ln

2

x)

1

1

9

π 2

sincos3 xx dx

0

(2x+3)2−x dx

∫

∫

π 6

−1

139

10	π2						9							dx							e
	∫																				∫xln xdx
														2
	0										x cos								x		1
11	3										xdx										3						x
	∫																	;			∫(3 − x)e							dx
							(							2	)	3
	1
								1 + x													2
12	e	(1+ lnx )dx																			1
	∫																				∫x6−x dx
	1																		x		0
13	2						exdx														2		3
	∫																				∫x			ln xdx
				e				2 x			−1
	1																				1
	π 2																				1
14	∫12sin x cos xdx																				∫xarctg2xdx
	0																				0
																										Окончание табл. 15.1
	1 2									xdx											π
15	∫																				∫xsin xdx
										1 − x					2
	0																				0
	e										dx										π 2					π
16																						x			−		cos 2xdx
	∫1 x 1 + ln x
																					π∫4					2
17	∫e			cos(ln x)														dx			∫1 (x −1)e−xdx
	1										x										0
18	3									xdx											5
	∫															;					∫xexdx
										1 + x					2
	0																				0
19	∫2						x				1 + x2 dx										π∫xsin xdx
	3																				0
20	∫1						x2dx						;								∫1 arccosxdx
							6
	0	1+ x																			0
21	∫0										dx							;			∫2	(x +1)7x dx
																3
	−2 (1 − 2x)																				0
		2									xdx										π 2
22	∫																				∫ (x −1)cos 2xdx
											2
	2						3				x			−1							0
23	1							3		e	x4	dx									π / 2					π
	∫x																				∫		x +			2	sin xdx
	0																				0
24	e																				e
	∫sin (ln x)dx																				∫ln5x dx
	1																	x			1	х
25	3																				π
	∫x									9 − x2 dx											∫xsin 4xdx
	0																				0

140

26	3	3											1
	∫				1 + x3 x2dx								∫xe3x−1dx
	1												0
27		1											2
		∫			1 − x2 xdx								∫xarcсtg2xdx
	1		2										1
28	π 3				sin xdx								π 3
	∫												∫ xcos3xdx
				1 + cos x
	π 2													0
29	3				x2dx								1		2 x
	∫												∫x		3	dx
			(4 + x				3	)		2
	2												0
30	0,5				3	x							e	2
	−0,5∫								dx				∫е lnх7x dx
					1 +	9x

Задание 15.2. Найти площадь фигуры, ограниченной линиями (табл. 15.2):

Таблица 15.2. Распределение вариантов

Номер
варианта	y = x2 +3x −5; y = 2x +1
1
2	y = x2 + 2x −3; y =3x2 −4x +1
3	y = −2x2 +3x +1; y = 2x
4	y = −3x2 + 2x +1; y =3x +1
	y = x2 − x +1; y = 2x2 +3x +1
5
	y = x2 +5x +3; y = −4x2 +3x +3
6
	y =3x2 + 2x −1; y =3x +3
7
	y = x2 −5x −3; y = −x2 − х−3
8
	y =3x2 + 2x −1; y = x2 +5x −1
9
	y = −2x2 +3x +1; y = 2x +1
10
	y = x2 +5x +3; y = −4x2 +3x + 6
11
	y = x2 +3x −1; y = 2x2 +3x −5
12
	y = x2 − x −5; y = −x −1
13
	y = x2 + x −7; y = −2x2 +3x +1
14
	y = x2 − x +1; y = 2x2 +3x −4
15
	y = x2 − x −5; y = −x + 4
16

141

17			y = x2 −2x +5; y = −2x2 +3x +5
18			y = −x2 + 2x +3; y = x −3
19			y = 2x2 − x +1; y = x +1
20			y = x2 −3x + 4; y = −3x2 + 2x +3
21			y = x2 −5x +3; y = −x2 −7х+3
22			y = x2 +3x −5; y = 2x −3
23			y = x2 +3x + 4; y = 2x2 +5x +1
24			y = x2 + x −7; y = −2x2 +3x −2
25			y = −3x2 + 2x +1; y = 2x −2
26			y = x2 + 2x −3; y =3x2 −4x −3
							Окончание табл. 15.2
27			y = 2x2 − x +1; y = x +5
28			y = −x2 + 2x −3; y = x −5
29			y = x2 −3x + 4; y = −3x2 + 2x + 4
30			y = x2 −2x +5; y = −2x2 +3x +3
Задание 15.3. Найти объем тела, образованного вращением линии вокруг
соответствующей оси (табл. 15.3):
				Таблица 15.3. Распределение вариантов
Номер					Номер
варианта					варианта
1	y = ln x, x =1, x = e, Oх					16	y = x2 −1, y = 0, Oх
2	х = 9 у − 4, х =3, Oх					17	у =3 х, х = 2, Oх
3	х = 4 у −9, х =3, Oy					18	у = 9х, у = 2, Oy
4	у = 7х, х = 2, Oх					19	х = 9 у − 4, х =3, Oy
5	у = 2х, у =3, х = 0, Oy					20	y = ln x, x = e2 , x = e3 , Oх
6	y = x2 −5, y = 0, Oy					21	х = 6 у −4, х = 2, Oх
7	у =5х, у = 2, х = 0, Oy					22	y = x2 − 4, y = 0, Oy
8	y = x	2	−3,	y = 0, Oх		23	1	х
							у =	, х = 2, у = 0, Oх
							2

142

9	у = 2х, у = 3, Oy						24	х = 4 у−9, х =3, Oх
								у = 2х, х = 3, Oх
10	y = x2 −1, y =8, Oх						25
11		1		х			26			2	, Oх
	у =			, х = 5, у = 0, Oх				y = ln x, x = e, x = e
		3
									1	х
12	y =5x		2	−3,	y = 0,	Oy	27
								у =		, х = 3, у = 0, Oy
									2
								у =3х, у = 2, х = 0, Oy
13	y = x2 −3,				y = 0,	Oy	28
								у = 5х, у = 4, Oy
14	х =	6 у −4, х = 2, Oy					29
15	у =5х, х = 4, Oх						30	y = x2 −5, y = 0, Oх

143

РАЗДЕЛ 7

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

ТЕМА 1

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Основные понятия. Задача Коши

Дифференциальным уравнением

F (x, y, y′, y′′,....y(n) )= 0 .

n – го порядка называется уравнение вида:

(7.1)

Порядком дифференциального уравнения называется порядок наивысшей из производных, входящих в уравнение.

Решением или интегралом дифференциального уравнения называется та-

кая функция y =ϕ(x) , которая при подстановке его в уравнение вместе со свои-

ми производными, обращает его в тождество.

График решения называется интегральной кривой. Процесс нахождения решения называется интегрирование дифференциального уравнения.

Общим решением дифференциального уравнения n – го порядка называется функция вида

y =ϕ(x,C1,C2 ,...,Cn ) ,

(7.2)

где C1,C2 ,...,Cn – произвольные постоянные. Если решение дифференциального уравнения выражено в неявной форме f (x, y,C1,C2 ,...,Cn ) = 0 , то его называют

общим интегралом.

Начальными условиями дифференциального уравнения n – го порядка называются значения функции и ее (n −1) -ой производных в заданной точке x0 :

y(x0 ) = y0 , y′(x0 ) = y0′, y′′(x0 ) = y0′′,..., y(n−1) (x0 ) = y(n−1)0 .

(7.3)

Задача отыскания решения дифференциального уравнения (7.1), удовлетворяющего начальным условиям (7.3), называется задачей Коши.

Частным решением дифференциального уравнения, которое удовлетворяет начальным условиям, называется решение, полученное из общего решения (7.2) при подстановке в него фиксированных значений постоянных C1,C2 ,...,Cn , опре-

деленных с помощью системы

144

ϕ(x0 ,C1,C2 ,...,Cn )= y0 ,

ϕ′(x0 ,C1,C2 ,...,Cn )= y0′,

ϕ(n−1) (x0 ,C1,C2 ,...,Cn )= y0(n−1) .

Рассмотрим дифференциальные уравнения первого порядка. Дифференциальное уравнение вида

F (x, y, y′)= 0

называется дифференциальным уравнением первого порядка, не разрешенным относительно производной.

Соответственно уравнение вида

y′ = f (x, y)

называется дифференциальным уравнением первого порядка, разрешенным относительно производной.

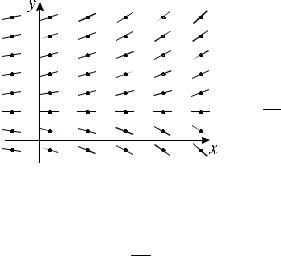
Дифференциальное уравнение определяет направление касательной в ка-

		ждой точке интегральной кривой. Совокупность
		этих направлений образует так называемое поле на-
		правлений уравнения (рис 7.1).
			x3	Пример 7.1. Проверить, что	функция
		y =		+C является решением дифференциального
			3
		уравнения y′= x2 .
Рис. 7.1				Решение. Действительно, подставив решение
в данное уравнение, получаем верное тождество:
	3	′
x		+C = x2 x2 ≡ x2 .
3
Дифференциальные уравнения с разделенными и
		разделяющимися переменными
Дифференциальное уравнение вида
f1(x)dx + f2 ( y)dy = 0 ,					(7.4)
где f1(x) и f2 ( y)		– заданные и непрерывные на некотором интервале функции,

называется дифференциальным уравнением с разделенными переменным.

145

Проинтегрировав обе части равенства (7.4) получаем общий интеграл вида

∫ f1(x)dx + ∫ f2 ( y)dy = C, C = const .	(7.5)
Примеры решения задач

Пример 7.2. Найти общее решение дифференциального уравнения

(1 + x)dx + y2dy = 0 .

Решение. Проинтегрировав обе части заданного уравнения, получаем

∫(1 + x)dx + ∫y2dy = 0 .

Отсюда находим общий интеграл

y3	+	(1	+ x)2	+C	= 0
3			2	1

Преобразовав последнее уравнение, находим общее решение исходного уравнения

y = 3 −3C −	3(1 + x)2	= 3 C −	3(1 + x)2		,
1	2			2
где С = −3C1 .
Уравнение вида
f1 (x)g1( y)dx + f2 (x)g2 ( y)dy = 0					(7.6)

называется дифференциальным уравнением с разделяющимися переменными.

Разделив переменные в уравнение (7.6), получим уравнение с разделенными переменными:

f1 (x)g1 ( y)dx + f2 (x)g2 ( y)dy = 0 : (g1 ( y) f2 (x))

	f1		(x)	dx +		g2 ( y)		dy = 0 .		(7.7)
			(x)
	f	2				g ( y)
				1
Проинтегрировав обе части уравнения (7.7), получим общий интеграл
	∫	f1 (x)			dx + ∫		g2 ( y)		dy = C,	C = const .
		f (x)					g ( y)
			2	1

145

Если функции f2 (x) и g1 ( y) обращаются в ноль при каких-либо значениях x1 и y1 соответственно, то x = x1 и y = y1 также являются интегралами урав-

нения (7.6).

Аналогично, дифференциальное уравнение

y′ = f1(x) f2 ( y)

(7.8)

является уравнением с разделяющимися переменными, его можно переписать следующим образом:

dy = f (x) f		2	( y)	dy	= f (x)dx .
dx	1			f2 ( y)	1

Следовательно, опять получаем уравнение с разделенными переменными. Пример 7.3. Найти общее решение уравнения 1 − y2 dx − ydy = 0 . Решение. Разделяя переменные, получаем

y

1 − y2 dx = −ydy

: 1 − y2 dx = −

dy .

1 − y2

Интегрируя обе части полученного равенства, находим

y

2

∫dx = − ∫

dy x +C = 1 ∫d (1 − y2 ) x +C = − 1− y2 .

1

− y

2

2

1 − y

Отсюда

(x +C )2 + y2 =1.

Заметим, что выражение

1 − y2 обращается в ноль при y = ±1. Следова-

тельно, функции y = ±1 также являются решением исходного уравнения.

Пример 7.4. Найти частное решение уравнения

y

′

y

, удовлетворяю-

= − x

щее начальному условию y(1) = 4 .

Решение. Так как y′

dy

, то уравнение принимает вид:

= dx

	dy	= −	y	или xdy = −ydx и	dy	= − dx .
	dx		x		y
						x

Отсюда, интегрируя, находим

146

∫dy	= −∫dx	ln | y |= −ln | x | +ln | C | ln | y |= ln	C	.	(7.9)
y	x		x

Заметим, что, если после интегрирования, получены выражения с логарифмами, то произвольную константу C , удобнее записывать в виде ln | C |.

Потенцируем последнее равенство в (7.9) и находим общее решение yo. p. исходного уравнения:

yo. p. = Cx .

Для того чтобы найти частное решение yч. р. , используем начальное усло-

вие y(1) = 4 :

4 = C1 С = 4 .

Значит, частное решение, удовлетворяющее заданному начальному условию, имеет вид

yч. р. = 4x .

Пример 7.5. Найти общее решение уравнения y′− y cos x = 2cos x .

Решение. С помощью простейших преобразований приведем уравнение к уравнению с разделяющимися переменными:

dydx = 2cos x + y cos x dy = cos x( y + 2)dx .

Делим обе части последнего уравнения на (y + 2), считая, что (y + 2)≠ 0 . Получаем уравнение с разделенными переменными

	dy		= cos xdx ,
	y +	2

откуда

∫ ydy+ 2 = ∫cos xdx ln y + 2 = sin x + ln C

или

ln y + 2 = ln Cesin x .

147