Исаченко Сопротивление материалов ч.1 2010

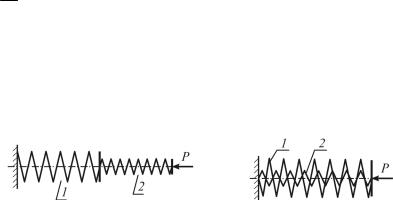
Деформация пружины λ (так называется осадка или растяжение

	пружины вдоль ее оси) определяется по формуле
		8D3n	λ = λ0 P ,	(6.19)
	где λ0 =		– податливость пружины (n –	число витков);
		Gd 4

1= с – жесткость пружины.

λ0

При

последовательном

соединении пружин (рис. 6.9)

λ0 = λ01 + λ02 ,

или

1

=

1

+

1

, а при параллельном соединении

с

с1

с2

(рис. 6.10)

1

=

1

+

1

, или с = с

+ с .

λ0

λ01

λ02

1

2

Рис. 6.9

Рис. 6.10

При большом шаге витка и d сопоставимыми с D можно рекомендовать формулу для τmax :

	τmax = k	Mкр	≤[τ] ,	(6.20)
		Wp

где k =	m + 0, 25	, m =	D	.
	m −1
			d

6.6. Задачи

Задача 6.1. Для вала, расчетная схема которого изображена на рис. 6.11, необходимо построить эпюры M x и ϕ и показать справедливость дифференциальной зависимости (6.11). Жесткость вала GJ p по всей длине одинакова.

271

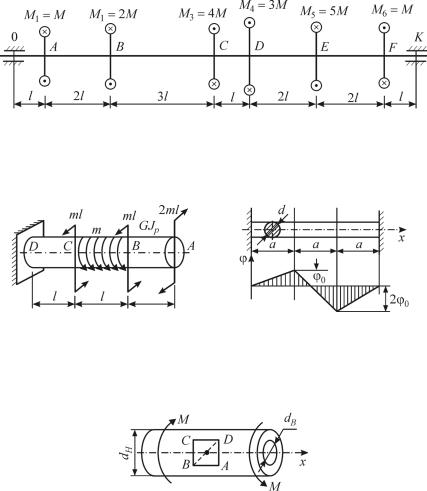
Рис. 6.11

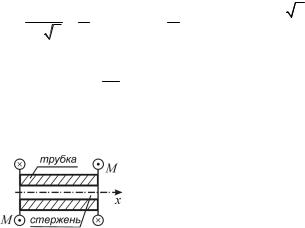
Задача 6.2. Для вала (рис. 6.12) определить угол закручивания сечения А. Известно GJ p , l, m.

Рис. 6.12

Рис. 6.13

Задача 6.3. По эпюре ϕ построить эпюру M x и определить значения внешних моментов (рис. 6.13), если а, J p , G, ϕ0 известны.

Рис. 6.14

Задача 6.4. На поверхности полого вала		dв	=α	нанесен
	dн
квадрат со стороной а (рис. 6.14). При действии момента M диаго-
наль квадрата BD укорачивается на величину	. Определить глав-
272

ные напряжения для точек около внутренней поверхности вала, если а, α, G, M заданы.

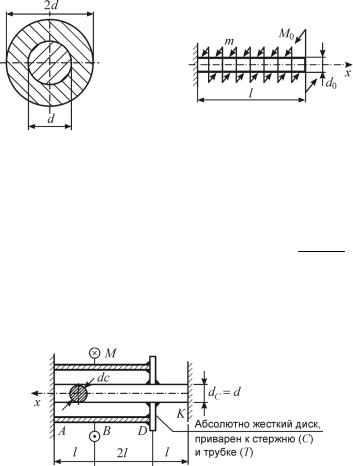
Задача 6.5. Круглый вал выполнен из стального круглого стержня и медной трубки, жестко соединенных между собой. Построить эпюру τ по перечному сечению, если вал скручивается моментом M (рис. 6.15).

Рис. 6.15

Рис. 6.16

Задача 6.6. Найти форму равного сопротивления для вала, скручиваемого сосредоточенным моментом M0 и распределенным m

[нм/м] (рис. 6.16), если d0 , M0 , m, [τ] заданы.

Задача 6.7. В каком отношении находятся (τmax )с , если

(τmax )т

(dв)т = 2dс , (dн)т = 2, 4dc , Gc = 2Gт , l = 4dc , M приложен к трубке (рис. 6.17), (dв)т и (dн)т – внутренний и наружный диаметр труб-

ки соответственно?

Рис. 6.17

273

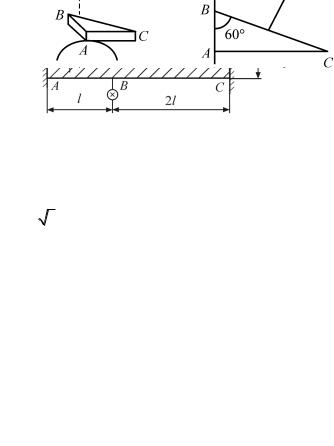
Задача 6.8. Определить отношение τmax на участках AB и BC, не раскрывая статической неопределимости (рис. 6.18).

Рис. 6.18

Задача 6.9. Полый ступенчатый вал скручивается моментом M (рис. 6.19). У точки A, лежащей вблизи внутренней поверхности, на наклонной площадке BC действует по нормали n напряжение, рав-

ное минус 25 3 МПа. Определить величину и направление M.

Рис. 6.19

Задача 6.10. Определить τmax в валике и трубке после сборки

узла. Порядок сборки: на валик с дисковыми выступами свободно без трения надевается трубка, из того же материала, что и валик; валик скручивается моментом M (возникающие в нем при этом напряжения меньше предела пропорциональности); концы трубки привариваются к выступам валика, после чего моменты M снима-

274

ются. По сравнению с валиком и трубкой дисковые выступы можно считать абсолютно жесткими (рис. 6.20).

Рис. 6.20

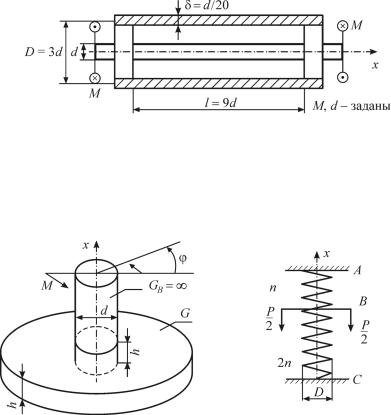
Задача 6.11. Жесткий вал заделан нижним концом в упругую плиту неограниченных размеров на глубину h (рис. 6.21). На какой угол ϕ повернется вал при нагружении моментом M, если в соединении с плитой проскальзывание отсутствует? G, h, d, M известны.

Рис. 6.21	Рис. 6.22
Задача 6.12. Определить τmax	и смещение по оси х сечения B

пружины (рис. 6.22), если известно P, D, n (число витков), d (диаметр проволоки пружины), G – модуль сдвига.

Задача 6.13. Из условия равнопрочности пружин подобрать диаметры их проволоки, если число витков n во всех пружинах одинаково, [τ] = 500 МПа. Весом абсолютно жесткой балки (рис. 6. 23) пренебрегаем.

275

Рис. 6.23

6.7.Решения, указания, ответы

6.1.Нарис. 6.24, апредставленаэпюра M x . Накаждомучастке M x определялось, как сумма моментов, лежащих по одну сторону от сече-

ния. Так, научасткеCD M x(CD) = M1 + M2 − M3 = −M (см. рис. 6.11).

Рис. 6.24

Эпюра углов закручивания представлена на рис. 6.24, б. В каждом характерном сечении угол закручивания определялся следующим образом:

276

ϕB =	M 2l			= 2Mk ,		k =	l	;
	GJ p						GJ p
ϕ = ϕ		B	+		3M 3l	=11Mk ;
C					GJ p

ϕD = ϕB +	(−M ) l	=10Mk и т.д.
	GJ p

Соответствие эпюры ϕ с эпюрой M x , согласно формуле (6.11),

представлено величинами углов ψ на рис. 6.24, б.

6.2. Решение выполним с помощью интеграла Мора (с использованием способа Верещагина). На рис. 6.25, а изображена расчетная схема; на рис. 6.25, б представлена эпюра M x от заданных на-

грузок (грузовая площадь); единичная система представлена на рис. 6.25, в; эпюра крутящего момента для единичной системы изображена на рис. 6.25, г.

По способу Верещагина

ϕA = GJ1 p (ω1MC1 +ω2 MC2

=1 ml l 1 − 1 ml l 1 − 2ml GJ p 2

+ω3MC3 ) =

l 1 = − 3 ml2 .

2 GJ p

Отметим, что в данном решении не было необходимости определять положения центров тяжести грузовых площадей ω, так как где бы они ни находились, им везде соответствует M x =1 .

6.3. В соответствии с рис. 6.26,

а выразим крутящие моменты

M x через углы закручивания:

GJ p

ϕ

x =a

=

M xa

= ϕ

0

M

x

= ϕ k , где k =

;

GJ p

0

a

1

1

M x

(x2

− a)

ϕ

x

= ϕ +

2

при x

= 2a , ϕ

x

= −2ϕ ,

0

GJ p

2

2

0

2

откуда M x

= −3ϕk ;

2

277

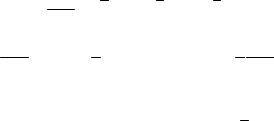
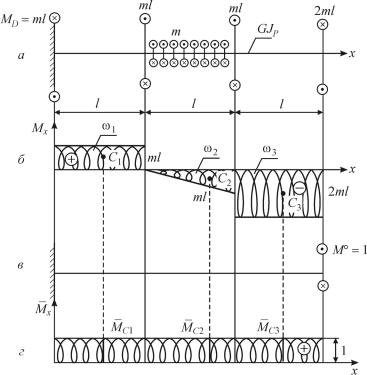
Рис. 6.25

Эпюра M x показана на рис. 6.26, б. Из эпюры M x следует, что: M A = ϕ0k и направлена по часовой стрелке (взгляд со стороны оси x); MB = −4ϕ0k и направлена против часовой стрелки; MC = 5ϕ0k и направлена по часовой стрелке; MD = −2ϕ0k и направлена против часовой стрелки (см. рис. 6.26, в). Осуществим проверку: для эквивалентной системы (рис. 6.26, г) угол ϕD должен быть равен нулю:

ϕD = −	4ϕ0k a	+	5ϕ0k 2a	−	2ϕ0k 3a	= 0 !
	GJ p		GJ p		GJ p
			278

Рис. 6.26

Рис. 6.27

6.4. Изобразим напряженное состояние элементарного объема с основанием в виде квадрата у наружной поверхности вала

(рис. 6.27, а):

279

εBD = − a / 2 = E1 (σ3 −μσ1) = E1 (−ε−μτ) τ = a(12+μE) .

Из рис. 6.27, б найдем искомые напряжения:

τ′ = τ dв , σ1′ = τ′, σ′3 = −τ′! dн

6.5. Вариант 1. Для стали Gс = 2Gм меди. Расчетная схема представлена на рис. 6.28.

Рис. 6.28

∑mx = 0 , M − Mc − Mм = 0 ,

т.е. задача один раз статически неопределимая. Теперь

Θ

с

=

Mc

= Θ

м

=

Mм

,

G J c

G J м

c

p

м p

c

πd 4

,

м

=

π(2d)4

−

πd 4

, откуда Mм = 7,5Mc , и с учетом

где J p =

32

J p

32

32

п. 1 Mc =

10

M , Mм =

75

M .

85

85

Тогда

d

τcxt(max) =

Mc 2

=

30

A , где A =

32M

;

6

85πd3

J cp

d

τмxt =

Mм 2

=

15

A

при ρ = d / 2 ;

J мp

6

τмxt(max) =

30

A при ρ = d .

6

280