Приклад 4.

Знайти у'', якщо 2х+5у³-4у+х²=0.

Розв’язання.

Продиференціюємо задану рівність по х і знайдемо у' : 2+15у² у' - 4 у'+2х=0 у'=. Отриману рівність ще раз продиференціюємо по х: у''= у''= у''=-

у''= -.

Виведе­мо формулу для похідної другого порядку параметрично заданої функції. Нехай функція y=f(x) задана параметрично рівняннями х = х(t), у = у(t), t( t_о,t₁ ), які в інтервалі ( t_о,t₁ ) мають похідні до другого порядку включно і х′(t)0. Оскільки , то маємо формулу для похідної другого порядку:

Приклад 5.

Знайти , якщоx=lnt, y=2t³.

Розв’язання.

Знайдемо похідні функцій, які записані у формулі: х'_t=; x''_t=-; y'_t=6t²; y''_t=12t. Маємо =.

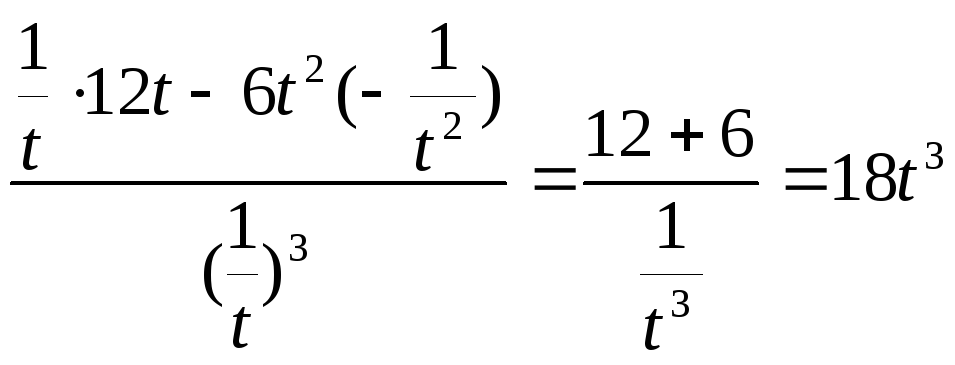Розглянемо на деякому проміжку (а; b) функцію у=f(х), яка на цьо­му проміжку має похідні до n-го порядку включно. Тоді для такої функції в кожній точці проміжку (а;b) існує диференціал

dy=f ′(x)dx

Диференціал першого порядку при фіксованому dх є функцією х, і якщо ця функція диференційовна на проміжку (а;b), то вона має диференціал. Цей диференціал називають диференціалом другого порядку:

d²y=d(dy) (читають: де два ігрек).

Підставимо в цю рівність dy . Матимемо: d²y=d(f′(x)dx)=(f′(x)dx)′dx

Оскільки dх як приріст аргументу є величина стала, то його можна виносити за знак операції диференціювання. Тоді

d²y=f′′(x)dx², dx²=dxdx

Взагалі, якщо для функції у=f(х) уже означений диференціал (п-1)-го порядку ((п-1)-й диференціал), то диференціалом п-го порядку, або п-м диференціалом функції у=f(х), називають диференціал першого порядку диференціала (п-1)-го порядку. Диференціал n-го порядку позначають символом d^пу.

Використовуючи формулу диференціала першого порядку, можна методом математичної індукції вивести формулу для d ^пу: dⁿy=f⁽ⁿ⁾(x)dxⁿ

Приклад 6.

Знайти d²y, якщо y=cos6x.

Розв’язання.

За формулою для знаходження d²y обчислимо у'': у'=-6sin6x, y''=-36cos6x. Тоді

d²y =-36cos6xdx².

При розгляді диференціала першого порядку було доведено його інваріантну властивість: форма диференціала не змінюється і тоді, коли аргумент функції f (х) є деякою функцією від t: х=и(t).

Виявляється, що диференціали вищих порядків такої властивості не мають. Покажемо це на прикладі диференціала другого порядку. Нехай маємо складену функцію у=f(х), х=и(t), де функції f(x) і и(t), мають похідні по своїх аргументах до другого порядку включно. Тоді f(х) має диференціал dy=f ′(x)dx, де f' (х) — похідна по аргументу х, а dх=и′(t)dt. Знайдемо d²у. Згідно з означенням, d²y=d(f′(x)dx)

Оскільки диференціал першого порядку має інваріантну власти­вість, то

d(f ′(x)dx)=d(f ′(x))dx+f ′(x)d(dx)=f ′′_xx(x)dx²+f ′_x(x)d²x

Остаточно дістаємо d²y =f ′′_xx(x)dx²+f ′_x(x)и′′(t) dt²

Бачимо, що формула диферен­ціала другого порядку змінюється. У формулі є новий доданок.

Отже, диференціал другого порядку інваріантної властивості не має.

Тема 3. Теореми про середнє. Правила Лопіталя.

1. Теорема Ферма.

2. Теорема Ролля. Її геометрична інтерпретація.

3. Теорема Лагранжа та наслідки.

4. Теорема Коші.

5. Невизначеність виду . Перше правило Лопіталя.

6. Невизначеність виду . Друге правило Лопіталя.

7. Невизначеність інших видів.