7. Порівняння нескінченно малих функцій. Еквівалентні нескінченно малі функції.

Означення 2.8. Функція α(x) називається нескінченно малою при х→х_0, якщо для довільного ε>0 існує δ(ε)>0 (М>0), що для всіх х таких, що (|x|>M), виконується нерівність |α(x)|<ε.

Означення 2.9. Функція f(x) називається нескінченно великою при х→∞_, якщо для довільного М>0 існує таке число N=N(М)>0, що для всіх х таких, що (|x|>M), виконується нерівність |f(x)|>M.

Дві нескінченно малі функції порівнюють між собою за допомогою дослідження їхнього відношення. Нехай α₁(х) та α₂(х) нескінченно малі функції при х→х₀, тобто та.

Введемо такі означення 2.10:

1) функції α₁(х) та α₂(х) називають нескінченно малими одного порядку при х→х₀, якщо ;

2) функції α₁(х) називають нескінченно малою вищого порядку, ніж α₂(х) при х→х₀, якщо ;

3) функції α₁(х) називають нескінченно малою нижчого порядку, ніж α₂(х) при х→х₀, якщо ;

4) функції α₁(х) називають нескінченно малою к-го порядку відносно α₂(х) при х→х₀, якщо ;

5) нескінченно малі функції α₁(х) та α₂(х) називають непорівнянними при х→х₀, якщо в точці х₀ не існує границі їхнього відношення.

Аналогічно порівнюються нескінченно великі величини.

Приклад 6.

Порівняти нескінченно малі величини при х→0:

а) α₁(х)=х та α₂(х)=sin5x в) α₁(х)=1-cos4х та α₂(х)= x

б) α₁(х)=х² та α₂(х)=tgx г) α₁(х)=х та α₂(х)=x sin(1\x)

Розв'язання.

Знаходимо границю відношення нескінченно малих величин

а) , томуα₁(х) та α₂(х) нескінченно малі одного порядку.

б) 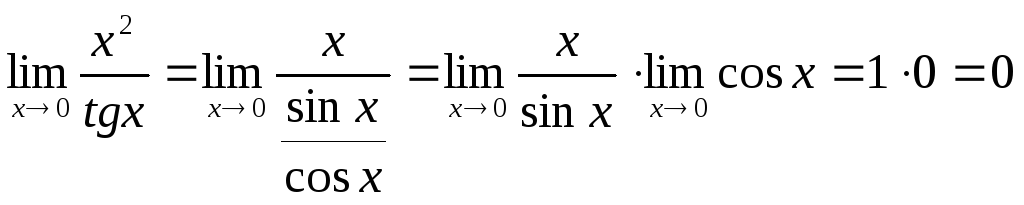, томуα₁(х) нескінченно мала вищого порядку, ніж α₂(х).

в) томуα₁(х) є нескінченно малою 2-го порядку.

г) 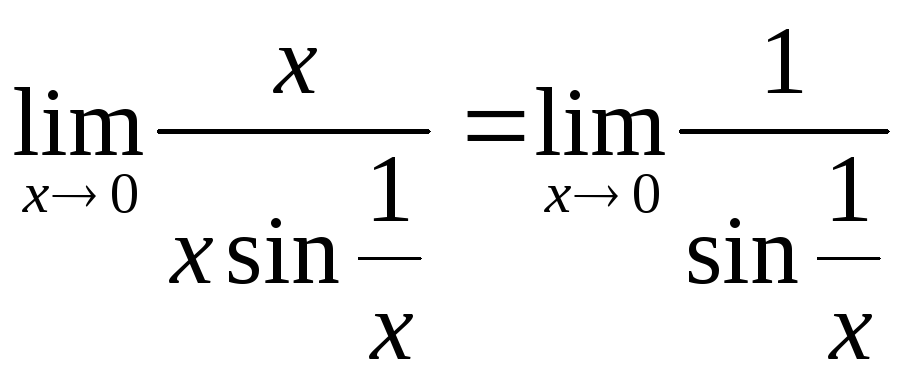не існує, томуα₁(х) та α₂(х) є непорівнянними.

Означення 2.11. Функції α₁(х) та α₂(х) - нескінченно малі функції при х→х₀ називають еквівалентними нескінченно малими, якщо , позначаютьα₁(х) ~ α₂(х).

Властивості еквівалентних нескінченно малих функцій.

Теорема 2.9. Нескінченно малі функції α₁(х) та α₂(х) еквівалентні при х→х₀ тоді і тільки тоді, коли різниця α₁(х)-α₂(х) є нескінченно малою вищого порядку, ніж кожна з функцій α₁(х) та α₂(х).

Доведення. Необхідність. Нехай α₁(х) та α₂(х) еквівалентні при х→х₀, тобто , тоді

Аналогічно . Отжеα₁(х)-α₂(х) є нескінченно малою вищого порядку, ніж кожна з функцій α₁(х) та α₂(х).

Достатність. Нехай α₁(х)-α₂(х) є нескінченно малою вищого порядку, ніж кожна з функцій α₁(х) та α₂(х), тобто .

Якщо , тозвідки, тобтоα₁(х) та α₂(х) еквівалентні при х→х_{0 .} Якщо , тозвідки, тобтоα₁(х) та α₂(х) еквівалентні при х→х_{0 .} Що й треба було довести.

Теорема 2.10. Нехай α₁(х) та α₁'(х)_, α₂(х) та α'₂(х) еквівалентні при х→х_{0 .} Якщо існує , то існує й, які рівні між собою.

Доведення. Маємо:

Що й треба було довести.

Ця теорема дає змогу при знаходженні границі відношення двох заданих нескінченно малих функцій кожну з них (або тільки одну) заміняти іншою нескінченно малою, яка еквівалентна заданій. Справедливим є такі еквівалентності:

якщо х→0, то ,.

Теорема 2.11. Сума скінченого числа нескінченно малих функцій різних порядків еквівалентна доданку нижчого порядку.

Доведення. Доведемо для двох функцій. α₁(х)→0 та α₂(х)→0 при х→х₀ , причому α₁(х) нескінченно мала функція вищого порядку, ніж α₂(х) при х→х₀, тобто , тоді, отже,α₁(х)+α₂(х)~α₂(х), х→х_{0 .} Що й треба було довести.