§3.5. Действия над случайными величинами и основные числовые характеристики

Две случайные величины X и Y называются независимыми, если закон распределения одной из них не зависит от того, какие значения приняла другая случайная величина. Если через x_i обозначим возможные значения случайной величины X, а через y_j — возможные значения случайной величины Y, то независимость случайных величин означает независимость событий {Х = x_i} и {Y = y_j} для любой комбинации индексов i и j.

Произведением случайных величин X и Y называется случайная величина, которая определяется по следующему правилу: возможные значения — произведение возможных значений x_i и y_j; вероятности появления — произведение соответствующих вероятностей. Полученную совокупность возможных значений величины XY необходимо упорядочить по возрастанию. Если среди получившейся совокупности значений есть одинаковые, то оставляем только разные, а соответствующие вероятности суммируем.

Пример.

Заданы законы распределения случайных величин X и Y.

X	-1	0	1
P	0,2	0,3	0,5

Y	-1	1	2
P	0,1	0,3	0,6

Найдем закон распределения для Z=XY:

XY	-2	-1	0	1	2
P	0,12	0,11	0,3	0,17	0,3

Суммой независимых случайных величин X и Y называется случайная величина, которая определяется по следующему правилу: возможные значения — сумма возможных значений x_i и y_j; вероятности появления — произведение соответствующих вероятностей. Полученную совокупность возможных значений величины X + Y необходимо упорядочить по возрастанию. Если среди получившейся совокупности значений есть одинаковые, то оставляем только разные, а соответствующие вероятности суммируем.

Пример.

Заданы законы распределения случайных величин X и Y.

X	-1	0	1
P	0,2	0,3	0,5

Y	-1	1	2
P	0,1	0,3	0,6

Найдем закон распределения для Z=X+Y:

X+Y	-2	-1	0	1	2	3
P	0,02	0,03	0,11	0,21	0,33	0,3

Если дискретная случайная величина Y является функцией от дискретной случайной величины X, т. е. Y = f (X), то закон распределения для Y можно получить по следующему правилу:

Y	f (x1)	f (x2)	…	f (xn)
pi	p1	p2	…	pn

Пример.

Задан закон распределения случайной величины X.

X	1	2	3
P	0,2	0,3	0,5

Тогда законы распределения случайных величин Y=X²иZ=2X-1 представлены ниже.

Y	1	4	9
P	0,2	0,3	0,5

Z	1	3	5
P	0,2	0,3	0,5

Закон распределения полностью характеризует случайную величину. Но он не всегда известен. Существуют некоторые числовые характеристики, описывающие случайную величину суммарно. К ним относятся математическое ожидание, дисперсия, начальные и центральные моменты.

Математическим ожиданием случайной величины Х называется ее среднее значение, вычисляемое по формулам: — для дискретной случайной величины; − для непрерывной случайной величины.

Свойства математического ожидания случайной величины:

1.  Математическое ожидание постоянной величины равно ей самой, т. е. M [C] = C;

2.  Постоянный множитель можно выносить за знак математического ожидания, т. е. M [CX] = = C M [X];

3.  Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий, т. е. М [X Y] = M [X] M [Y];

4. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий, т. е. М [X + Y] = M [X] + M [Y].

Математическое ожидание случайной величины X, имеющей биномиальное распределение (схема испытаний Бернулли), равно произведению числа испытаний на вероятность появления события в одном испытании, т. е. М [X] = n · p.

Пример.

Найти математическое ожидание суммы числа очков, которые выпадут при бросании двух игральных костей.

Законы распределения для случайных величин X и Y примут вид

1	2	3	4	5	6
1/6	1/6	1/6	1/6	1/6	1/6

Тогда M[X]=M[Y]=11/6+21/6+…+61/6=7/2.

По свойству 4 имеем: M[X+Y]=M[X]+M[Y]=7/2+7/2=7.

Знание математического ожидания случайной величины еще полностью не характеризует эту случайную величину. По этому числу нельзя еще судить ни о возможных значениях случайной величины, ни о том, как эти значения рассеяны вокруг математического ожидания.

Пример.

Заданы две случайные величины XиY.

X	-0,01	0,01
P	0,5	0,5

Y	-100	100
P	0,5	0,5

Найдем их математические ожидания M[X]= -0,010,5+ 0,010,5=0;

M[Y]=-1000,5+1000,5=0.

Как видно из примера, случайные величины имеют разные возможные значения, но одинаковые математические ожидания, причем случайная величина X имеет возможные значения близкие к M[X], а случайная величина Y  далекие. Здесь налицо малое и большое рассеяние возможных значений вокруг среднего. Для оценки величины рассеяния используют новую числовую характеристику  дисперсию дискретной случайной величины.

Введем понятие отклонения случайной величины от ее математического ожидания. Пусть X  случайная величина; M[X]  ее математическое ожидание. Рассмотрим новую случайную величину X-M[X]

Отклонением называют разность между случайной величиной и ее математическим ожиданием.

Отклонение имеет следующее важное свойство: математическое ожидание отклонения равно нулю, т. е. M [X – M [X]] = 0.

Для оценки величины рассеяния, казалось бы, проще всего вычислить все возможные значения отклонения случайной величины, а затем найти их среднее значение. Но это не подходит, т.к. согласно предыдущему свойству эта величина всегда равна нулю для любой случайной величины. Это следует из того, что одни значения отклонения будут больше, а другие меньше нуля. Следовательно, нужно оценивать абсолютные значения отклонения или их квадраты.

Дисперсией дискретной случайной величины Х называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: D [X] = M [X – M [X]]².

Если случайная величина задана законом распределения,

xi	x1	x2	…	xn
pi	p1	p2		pn

то дисперсию вычислим по формуле .Для непрерывной случайной величины . Здесь.

Пример.

Найти дисперсию случайной величины X, заданную следующим законом распределения:

X	1	2	5
P	0,3	0,5	0,2

M[X]= 10,3+ 20,5+ 50,2=2,3;

(x₁ – M[X])²=(1-2,3)²=1,69;

(x₂ – M[X])²=(2-2,3)²=0,09;

(x₃ – M[X])²=(5-2,3)²=7,29;

D[X]=1,690,3+0,090,5+7,290,2=2,01.

Более простая формула для вычисления дисперсии имеет вид: D [ X ] = M [ X ²] – (M [ X ])². Поясним ее применение на предыдущем примере. Для ее использования необходимо составить закон распределения случайной величины X²:

X ^2	1	4	25
P	0,3	0,5	0,2

M[X²]= 10,3 + 40,5 + 250,2 = 7,3; D[X]=7,3-(2,3)²=2,01.

Использование этой формулы существенно сокращает число арифметических действий.

Дисперсия D [X] кратко обозначается D_x .

Свойства дисперсии случайной величины:

1. Дисперсия постоянной величины равна нулю, т. е. D [C] = 0;

2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат, т. е. D [CX] = = C ² D [X];

3. Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий, т. е.  D [X + Y] = D [X] + D [Y];

4. Дисперсия суммы постоянной величины и случайной величины равна дисперсии случайной величины, т. е. сдвиг возможных значений случайной величины не изменяет рассеяния: D [C + X] = D [X];

5. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий, т. е.  D [X – Y] = D [X] + D [Y]. Действительно, D [X – Y] = D [X] + D [–Y] = D [X] +(–1)²·D [Y].

Недостатком дисперсии является то, что она имеет размерность, равную квадрату размерности случайной величины. Если это существенно в эксперименте, то используют другую числовую характеристику, среднее квадратическое отклонение.

Средним квадратическим отклонением случайной величины Х называется корень квадратный из дисперсии .

Модой дискретной случайной величины является ее наиболее вероятное значение.

Модой непрерывной случайной величины с плотностьюявляется то ее значение, при котором функциядостигает максимума.

Медианой случайной величины является такое ее значение, для которого одинаково вероятно, окажется ли случайная величины меньшеили больше, т. е..

Математическое ожидание случайной величины Х, распределенной по биномиальному закону, равно , а дисперсия .

Математическое ожидание и дисперсия случайной величины Х, распределенной по закону Пуассона, равны параметру закона т_x =λ; D_x =λ.

Математическое ожидание случайной величины Х, имеющей геометрическое распределение, равно т_x =1/p; и дисперсия D_x =(1-p)/p².

Математическое ожидание и дисперсия случайной величины, распределенной равномерно на участке ( ), равны

Математическое ожидание случайной величины Х, распределенной по нормальному закону, равно т_x = т, а дисперсия D_x = ²

Примеры:

1. Сделано два высоко рисковых вклада — 20 млн руб. в компанию и 18 млн руб. в компанию. Компанияобещает 40 % годовых, но может обанкротиться с вероятностью 0,3, компанияобещает 30 % годовых, но может обанкротиться с вероятностью 0,2. Будем считать, что банкротства компаний независимы. Составить ряд распределения случайной величиныX, равной сумме вкладов, полученных от двух компаний через год. Найти математическое ожидание и дисперсию случайной величины X.

Согласно условию задачи случайная величина X может принимать следующие значения:

= 0, если обе компании обанкротятся;

, если обанкротится только компания B;

, если обанкротится только компания A;

, если ни одна из компаний не обанкротится.

Для построения ряда распределения случайной величины X достаточно найти вероятности событий . Рассмотрим дополнительно следующие события:= {компанияобанкротится},= {компанияобанкротится}. Тогда. Согласно формуле умножения вероятностей, а также учитывая независимость событийи, будем иметь. Аналогично найдем вероятности оставшихся событий. Имея в виду, что событияитак же независимы, как и событияи, получим:

,

,

.

Таким образом, имеем ряд распределения случайной величины .

X	0,00	23,40	28,00	51,40
	0,06	0,24	0,14	0,56

По определению математическое ожидание случайной величины X может быть найдено следующим образом: . Найдем также дисперсию случайной величиныX : .

2. Найти квантиль уровня для случайной величиныX, заданной плотность вероятности вида .

На отрезке [0,1] функция распределения случайной величины X имеет вид , и поэтому является непрерывной и строго монотонной на отрезке [0, 1]. В соответствии со свойством квантили находимиз уравнения, откуда=.

3. Страховая компания заключает однотипные договоры, причем страховая премия (сумма, выплачиваемая страхуемым при заключении договора) составляет 4 тыс. рублей. При наступлении страхового случая компания должна выплатить 20 тыс. рублей. Известно, что страховой случай наступает в 4 % случаев. Фирме удалось застраховать 200 клиентов. Каков средний доход фирмы и среднеквадратическое отклонение дохода фирмы?

Обозначим через X − случайную величину, равную количеству клиентов, которым страховая компания будет делать выплаты по страховому случаю. Так как страховой случай наступает в 4 % случаев, то вероятность того, что он наступит при работе с одним конкретным клиентом составляет 0,04. Поэтому случайная величина X имеет биномиальный закон распределения с параметрами и. Обозначим черезY случайную величину, равную доходу фирмы. Согласно условию задачи случайная величина Y связана с X следующим образом: .

Воспользуемся свойствами математического ожидания и дисперсии для нахождения и: ,

. Известно, что для биномиального закона распределения , а.

Получаем , а. Таким образом, среднеквадратическое отклонение дохода фирмы равноруб.

4. Если соблюдается график движения, то среднее время ожидания пассажиром трамвая равно 3,5 минуты. Известно, что время ожидания имеет равномерный закон распределения. Минимальное время ожидания равно 0. Найти вероятность того, что пассажир будет ожидать трамвай от двух до пяти минут.

Обозначим время ожидания трамвая через X. Согласно условию задачи X равномерно распределена на интервале , где, а. Найдем параметры закона распределения, решив следующую систему уравнений:. Получаем, что второй параметр закона распределения. Тогда, где плотность распределения случайной величины имеет вид . Получаем

5. Рост взрослого мужчины удовлетворительно описывается нормальным законом распределения. По статистике средний рост составляет 175 см, а среднеквадратическое отклонение равно 7 см. Найти вероятность того, что рост наугад взятого мужчины будет отличаться от среднего роста не больше чем на 7 см.

Обозначим рост наугад взятого взрослого мужчины через X. По условию задачи X имеет нормальное распределение с параметрами , а. Требуется определить. Так как интервалсимметричен относительно, то.

6. Банк выдал кредит 10 млн рублей на год под залог жилого дома под 8 % годовых. Для уменьшения риска банк приобрел страховой полис на 20 млн. рублей, заплатив 3 % от страховой суммы. В страховой компании вероятность сгореть дому такого типа за год оценивают в 0,01 (в этом случае заемщик не вернет банку ничего). Найти средний доход банка.

Пусть X есть случайная величина, равная доходу банка. Через Y обозначим случайную величину, равную доходу, который приносит дом. Тогда , гдеY имеет следующий закон распределения:

	Дом не сгорит	Дом сгорит
Y	0,8	20 – 10
	0,99	0,01

Следовательно, .

Средний ожидаемый доход .

7. Согласно американским статистическим таблицам смертности вероятность того, что 25-летний человек проживет еще год, равна 0,992. Страховая компания предлагает такому человеку застраховать свою жизнь на год на сумму 1 000 долл., причем страховой взнос равен 10 долл. Найти математическое ожидание прибыли компании.

Величина прибыли X есть случайная величина со значениями 10 долл. (если застрахованный человек не умрет) и –990 долл. (если он умрет). Тогда закон распределения этой случайной величины имеет вид.

X	10	–990
	0,992	0,008

Тогда . Ожидаемая средняя прибыль положительна, что дает возможность страховой компании продолжать дело, оставлять резервный капитал для выплаты страховых сумм, производить административные расходы, получать прибыль.

8. Дети затеяли интересную игру. В одной из трех совершенно одинаковых шкатулок спрятан красивый значок. Желающий отгадать выбирает любую шкатулку и проверяет, есть ли в ней значок. Если значка в ней не оказалось, он должен отвернуться. За его спиной шкатулки переставляют местами. Ему предлагают попытать счастье еще раз. Игра продолжается до обнаружения значка. Пусть X — число попыток до отгадывания. Найдите закон распределения случайной величины X, и.

В задаче производятся независимые испытания, в каждом из которых вероятность выбора шкатулки со спрятанным в ней значком равняется и, следовательно, вероятность выбора шкатулки без значка равняется. Испытания заканчиваются, как только будет выбрана шкатулка со значком. Таким образом, если шкатулка со значком выбрана вk-ом испытании, то в предшествующих испытаниях она не была выбрана. По теореме умножения вероятностей независимых событий. Данное распределение является геометрическим распределением, закон которого представлен следующей таблицей

	1	2	3	...		...
	1/3	2/9	4/27	...		...

Тогда ,.

9. Случайная величина X принимает три значения: –1, 0, 1. Составить ее закон распределения, если .

Обозначая искомые вероятности , приходим к следующему закону распределения случайной величины:

	–1	0	1

По условию задачи и. Заметим, что++=1. Для нахождения вероятностейполучаем следующую систему:.

Отсюда, решая ее, получим = 0,25;= 0,5;= 0,25.Закон распределения случайной величиныX имеет вид:

	-1	0	1
	0,25	0,5	0,25

10. Рабочий обслуживает четыре автоматические линии, действующие независимо друг от друга. Вероятности того, что в течение смены эти линии потребуют вмешательства рабочего, равны соответственно 0,3; 0,35; 0,4; 0,45. Найти математическое ожидание и дисперсию числа линий, которые потребуют вмешательства рабочего в течение смены.

Пусть — случайные величины, принимающие значения 1 и 0 в зависимости от того, потребует или не потребует вмешательства рабочего соответствующая автоматическая линия. Тогда законы распределения этих случайных величин выглядят следующим образом:

для

	1	0
	0,3	0,7

для

	1	0
	0,35	0,65

для

	1	0
	0,4	0,6

для

	1	0
	0,45	0,55

Следовательно, по формулам вычисления математического ожидания и дисперсии имеем:

. Аналогично Общее числоX линий, которые потребуют вмешательства рабочего, может быть представлено в виде суммы: . По свойству вычисления математического ожидания для суммы случайных величин имеем:.

Поскольку величины независимы, то

.

11. Может ли случайная величина X иметь биномиальное распределение вероятностей, если: а) ; б).

а) Для биномиального распределения вероятностей , где— количество независимых испытаний,— вероятность успеха, а— вероятность неудачи. Для нахождения этих характеристик имеем систему уравнений. Разделив второе уравнение системы на первое, получимили. Из первого уравнения системы. Имеем серию из 12 независимых испытаний с вероятностью успеха равной, т. е. случайная величинаX имеет биномиальное распределение вероятностей.

б) В этом случае имеем систему уравнений . Разделив второе уравнение системы на первое, получимили. Из первого уравнения системы. Количество испытаний получилось дробным, значит, случайная величинаX в этом случае не имеет биномиального распределения.

12. Дана функция .

При каком значении параметра функцияявляется плотностью распределения случайной величиныX ? Определить функцию распределения и найти вероятность попаданияX в интервал .

Используем следующее свойство плотности распределения непрерывной случайной величины или в нашем случае.

Откуда , т. е..

Находим математическое ожидание по формуле

.Вычислим функцию распределения по формуле

.

Тогда .

Задания для самостоятельного решения на дискретные случайные величины:

1. У дежурного гостиницы в кармане восемь разных ключей от разных дверей. Вынув наугад ключ, он пробует открыть дверь ближайшей комнаты. Сколько раз в среднем ему придется пробовать открывать эту комнату, если: а) проверенный ключ кладется обратно в карман; б) проверенный ключ не кладется обратно в карман.

2. Дискретная случайная величина X принимает только три возможных значения: , причем. Вероятности того, чтоX примет значения исоответственно равны 0,3 и 0,2. Постройте закон распределения случайной величиныX, зная, что математическое ожидание равно 2,2 и дисперсия равна 0,76.

3. Задан закон распределения дискретной случайной величины с одной недостающей вероятностью . Построить график функции распределения случайной величины, вычислить ее математическое ожидание, дисперсию и среднеквадратическое отклонение.

4. Случайная величина X принимает три значения: –1, 0, 1. Составить ее ряд распределения, если =0,=0,5.

5. По заданной функции распределения случайной величиныX найдите 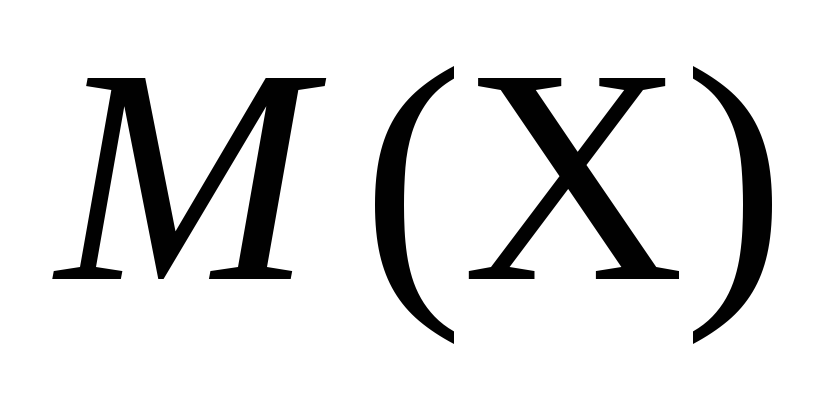и.

6. Какой наименьшей и какой наибольшей может быть дисперсия случайной величиныXс функцией распределения в зависимости от параметра?

7. Трое студентов независимо друг от друга сдают экзамен по математике на отлично с вероятностями 0,9, 0,8 и 0,7 соответственно. Пусть X — общее число полученных ими отличных оценок. Вычислите и.

8. Может ли случайная величина X иметь биномиальное распределение вероятностей, если: а) =6,=3; б)=7,=4.

9. Пусть X— число решек, Y — число орлов, выпадающих при шести бросаниях монеты. Пусть . ВычислитеM(Z).

10. Постройте график функции распределения случайной величины X, распределенной равномерно на множестве {–1, 0, 1}.

11. Пусть X — число успехов, а Y — число неудач в трех испытаниях Бернулли с вероятностью успеха в отдельном испытании . Постройте график функции распределения случайной величиныи вычислитеM(Z).

12. Случайная величина X имеет геометрическое распределение вероятностей с параметром . Чему равна вероятность того, чтоX примет четное значение?

13. По пути движения автомобиля пять светофоров. Каждый из них, независимо от остальных светофоров, с вероятностью 0,5 запрещает движение. Пусть X — число светофоров, пройденных автомобилем до первой остановки. Найдите закон распределения случайной величины X и ее математическое ожидание.

14. Закон распределения случайной величины X выглядит следующим образом

X	–0,5	0	0,5	1	1,5
р	0,1	0,4	0,1	0,3	0,1

Построить ряды распределения и найти математическое ожидание следующих случайных величин: а) ; б); в).

Задания для самостоятельного решения на непрерывные случайные величины:

1. Плотность вероятности случайной величины X имеет следующий вид: .

Найти величину , функцию распределения случайной величиныX, и, а также моду и медиану распределения.

2. Случайная величина X имеет нормальное распределение вероятностей со средним значением 25. Вычислить вероятность попадания этой случайной величины в интервал (35, 40), если она попадает в интервал (20, 30) с вероятностью 0,2.

3. Найти квантиль уровня p=2/3 равномерного распределения на интервале (0, 1).

4. Найти квантиль уровня p=2/3 экспоненциального распределения с параметром =1.

5. Случайная величина X принимает положительные значения, имеет плотность вероятностей . Найти значение параметраи математическое ожидание случайной величиныX.

6. Случайная величина X, распределенная равномерно, имеет следующие числовые характеристики: =2,=3. Найти функцию распределения случайной величиныX.

7. Известно, что случайная величина X имеет равномерное распределение в интервале (а, b), причем ==3. Найдите числаa и b.

8. Годовой доход случайно выбранного налогоплательщика описывается случайной величиной X с плотностью распределения . Найти значение параметра, средний годовой доход и среднее квадратичное отклонение годового дохода. Определить размер годового доходаX_min, не ниже которого с вероятностью 0,6 окажется годовой доход случайно выбранного налогоплательщика.

9. Текущая цена акции может быть приближена нормальным распределением с математическим ожиданием 15,28 рублей и средним квадратичным отклонением 0,12 рублей. Рассчитать вероятности того, что цена акции окажется: а) не ниже 15,50 рублей; б) не выше 15,00 рублей; в) между 15,10 и 15,40 рублями; г) между 15,05 и 15,10 рублями.

10. Найти моду и медиану случайной величины X, которая имеет равномерное распределение в интервале (0, 5).

Задания для самостоятельного решения на биномиальное распределение:

В следующих задачах нужно: определить закон распределения случайной величины, найти числовые характеристики распределения, найти функцию распределения и построить ее график.

1. В городе шесть коммерческих банков. У каждого риск банкротства в течение года составляет 10 %. Чему равна вероятность того, что в течение года обанкротится не более одного банка? Случайная величина X — количество обанкротившихся банков.

2. Нефтеразведочная компания получила финансирование для проведения шести нефтеразведок, вероятность успешной нефтеразведки 0,05. Предположим, что работу осуществляют независимые друг от друга разведывательные партии. Чему равна вероятность того, что не менее двух нефтеразведок принесут успех? Случайная величина X — количество успешных нефтеразведок.

3. Хорошим считается руководитель, принимающий не менее 70 % правильных решений. Пусть управляющий банком — хороший руководитель, принимающий правильное решение с постоянной вероятностью 0,75. Такому управляющему банком предстоит принять решения по четырем важным вопросам банковской политики. Случайная величина X — количество правильных решений, принятых управляющим. Чему равна вероятность того, что управляющий примет не менее трех правильных решений?

4. В ходе аудиторской проверки строительной компании аудитор случайным образом отбирает пять счетов. Вероятность наличия ошибки в каждом счете — величина постоянная и равна 0,03. Случайная величина X — количество счетов с ошибкой. Какова вероятность того, что хотя бы один счет будет с ошибкой?

5. В банк поступило 30 авизо. Есть подозрение, что среди них три фальшивые. Тщательной проверке подвергаются пять случайно выбранных авизо. Случайная величина X — количество фальшивых авизо среди отобранных. Чему равна вероятность того, что в ходе проверки обнаружится менее двух фальшивок?

6. Записи страховой компании показали, что 30 % держателей страховых полисов старше 50 лет потребовали возмещения страховых сумм. Для проверки в случайном порядке отобраны пять человек старше 50 лет, имеющих полисы. Случайная величина X — количество потребующих возмещения среди отобранных. Чему равна вероятность того, что потребуют возмещения более трех человек?

7. Билет для зачета содержит пять вопросов, к каждому из которых приведено четыре возможных ответа (правильный ответ только один). Предположим, что студент выбирает ответы среди предложенных наугад. Случайная величина X — количество правильных ответов, угаданных студентом. Какова вероятность того, что он ответит правильно не менее чем на четыре вопроса?

8. Для того чтобы проверить точность своих финансовых счетов, компания регулярно пользуется услугами аудиторов. Предположим, что служащие компании при обработке входящих счетов допускают 5 % ошибок. Аудитор случайно отбирает три входящих документа. Случайная величина X — количество документов с ошибками среди отобранных. Какова вероятность того, что аудитор обнаружит более одного ошибочного документа среди отобранных?

9. Телевизионный канал рекламирует новый вид детского питания. Вероятность того, что телезритель увидит эту рекламу, оценивается в 0,2. Случайным образом отобраны шесть телезрителей. Случайная величина X — количество лиц, видевших рекламу, среди отобранных. Чему равна вероятность того, что, по крайней мере, два телезрителя из отобранных видели рекламу нового питания?

10. Торговый агент контактирует с семью потенциальными покупателями в день. Из опыта ему известно: вероятность того, что потенциальный покупатель совершит покупку, равна 0,1. Случайная величина X — количество покупателей, совершивших покупку после встречи с торговым агентом. Чему равна вероятность того, что хотя бы два посетителя сделают покупки?

Задания для самостоятельного решения на нормальное распределение:

1. Дневная добыча угля в некоторой шахте распределена по нормальному закону с математическим ожиданием 785 т и стандартным отклонением 60 т. Найдите вероятность того, что в определенный день будут добыты, по крайней мере, 800 т угля. Определите долю рабочих дней, в которые будет добыто от 750 т до 850 т угля. Найдите вероятность того, что в данный день добыча угля окажется ниже 665 т.

2. Вес тропического грейпфрута, выращенного в Краснодарском крае, нормально распределенная случайная величина с неизвестным математическим ожиданием и дисперсией, равной 0,04. Агрономы знают, что 65 % фруктов весят меньше чем 0,5 кг. Найдите ожидаемый вес случайно выбранного грейпфрута.

3. Предположим, что в течение года цена на акции некоторой компании есть случайная величина, распределенная по нормальному закону с математическим ожиданием, равным 48 долл., и стандартным отклонением, равным 6. Определите вероятность того, что в случайно выбранный день обсуждаемого периода цена была: а) более 60 долл. за акцию; б) ниже 60 долл. за акцию; в) выше 40 долл. за акцию; г) между 40 и 50 долл. за акцию.

4. Технический отдел компании, производящей автопокрышки, планирует выпустить несколько партий покрышек и проверить степень их износа на тестирующем оборудовании. С этой целью предполагается увеличивать количество каучука в покрышках каждой следующей партии до тех пор, пока срок службы покрышек окажется приемлемым. Эксперимент показал, что стандартное отклонение срока службы покрышек фактически остается постоянным от партии к партии и составляет 2 500 миль. Если компания хочет, чтобы 80 % выпускаемых покрышек имели срок службы не менее 2 500 миль, то какой наименьший средний срок службы автопокрышек должен быть заложен в расчетах технического отдела? Считать срок службы автопокрышек нормально распределенным.

5. Менеджер торгово-посреднической фирмы получает жалобы от некоторых клиентов на то, что служащие фирмы затрачивают слишком много времени на выполнение их заказов. Собрав и проанализировав соответствующую информацию, он выяснил, что среднее время выполнения заказа составляет 6,6 дней, однако для выполнения 20 % заказов потребовалось 15 дней и более. Учитывая, что время выполнения заказа есть случайная величина, распределенная по нормальному закону, определите фактическое стандартное отклонение времени обслуживания клиентов.