
- •Российская академия народного хозяйства и государственной службы
- •Оглавление
- •Тема 1. Элементы комбинаторики
- •Контрольные вопросы и задания
- •Список основной литературы
- •Список дополнительной литературы
- •Тема 2. Случайные события §2.1. Классическое определение вероятности события
- •§2.2. Действия над событиями
- •§2.3. Теорема сложения вероятностей
- •§2.4. Понятие условной вероятности
- •§2.5. Теорема умножения вероятностей
- •§2.6. Формула полной вероятности и формула Байеса
- •§2.7. Повторение испытаний. Формула Бернулли
- •Контрольные вопросы и задания
- •Список основной литературы
- •Список дополнительной литературы
- •Тема 3. Случайные величины и их законы распределения §3.1. Общие определения
- •§3.2. Дискретные случайные величины и основные законы распределения
- •§3.3. Понятие интегральной и дифференциальной функции распределения
- •§3.4. Непрерывные случайные величины и основные законы распределения
- •§3.5. Действия над случайными величинами и основные числовые характеристики
- •§3.6. Неравенство Чебышева и интегральная теорема Муавра — Лапласа
- •Контрольные вопросы и задания
- •Список основной литературы
- •Список дополнительной литературы
- •Тема 4. Введение в математическую статистику §4.1 Основные определения
- •§4.2. Вариационный ряд и статистическое распределение выборки
- •§4.3. Графическое изображение статистического распределения
- •§ 4.4. Выборочные средние и методы их расчета
- •Контрольные вопросы и задания
- •Список основной литературы
- •Список дополнительной литературы
- •Тема 5. Статистические оценки параметров распределения §5.1 Точечные оценки
- •§ 5.2. Интервальные оценки
- •5.2.1. Доверительные интервалы для оценки параметров m и σ2 нормально распределенной генеральной совокупности
- •5.2.2. Доверительные интервалы для оценки разности средних двух нормально распределенных генеральных совокупностей
- •5.2.3. Доверительные интервалы для оценки доли признака
- •Контрольные вопросы и задания
- •Список основной литературы
- •Список дополнительной литературы
- •Тема 6. Статистические гипотезы § 6.1. Основные понятия статистической проверки гипотез
- •§ 6.2. Проверка гипотезы о равенстве дисперсии нормально распределенной генеральной совокупности некоторому значению
- •§ 6.3. Проверка гипотезы о равенстве генеральной средней нормально распределенной генеральной совокупности некоторому значению
- •§ 6.4. Проверка гипотезы о доле признака
- •§ 6.5. Проверка гипотезы о виде распределения генеральной совокупности
- •§ 6.6. Проверка гипотезы о равенстве параметров двух нормально распределенных генеральных совокупностей
- •Контрольные вопросы и задания
- •Список основной литературы
- •Список дополнительной литературы
- •Приложение
- •Значения функции плотности стандартизированного нормального распределения n (0, 1)
- •Значения функции распределения f (0,1)(X) нормального закона n (0,1);
- •Распределение Пуассона
- •Квантили tp распределения Стьюдента
- •Квантили распределения 2(хи-квадрат)
- •Квантили распределения Фишера f0,99(k1, k2)
- •Квантили распределения Фишера f0,975(k1, k2).
- •Квантили распределения Фишера f0,95(k1, k2)
- •Квантили распределения Фишера f0,90(k1, k2)
- •Заключение
- •Евгений Алексеевич Рапоцевич теория вероятностей и мамематическая статистика Учебное пособие
- •630102, Г. Новосибирск, ул. Нижегородская, 6, СибАгс
§ 6.2. Проверка гипотезы о равенстве дисперсии нормально распределенной генеральной совокупности некоторому значению
Пусть
известно, что генеральная совокупность
распределена нормально. Кроме этого
есть основания предполагать, что
дисперсия равна некоторому значению
![]() .
Тогда выдвинем нулевую гипотезу
.
Тогда выдвинем нулевую гипотезу![]() «генеральная
дисперсия данной генеральной совокупности
равна гипотетическому (предполагаемому)
значению
«генеральная
дисперсия данной генеральной совокупности
равна гипотетическому (предполагаемому)
значению![]() ».
».
Возможны три случая
выдвижения альтернативной гипотезы:
![]() ;
;![]() ;
;![]() .
.
Для статистической
проверки нулевой гипотезы из генеральной
совокупности извлекают выборку объема
n. По этой выборке можно
рассчитать выборочную дисперсиюDви исправленную дисперсиюS2.
Необходимо проверить, значимо или
незначимо различаются исправленная
выборочная дисперсияS2и гипотетическая генеральная дисперсия![]() .
Для этого выберем некоторый уровень
значимости. Для
проверки нулевой гипотезы выберем
критерийслучайную
величину с известным законом распределения:
.
Для этого выберем некоторый уровень
значимости. Для
проверки нулевой гипотезы выберем
критерийслучайную
величину с известным законом распределения:![]() ,
имеющей распределение «хи-квадрат» сn-1степенями свободы. По
этому критерию и уровню значимости
строится критическая область. Как уже
говорилось ранее, вид критической
области зависит от выбора конкурирующей
гипотезы. Разберем возможные случаи:
,
имеющей распределение «хи-квадрат» сn-1степенями свободы. По
этому критерию и уровню значимости
строится критическая область. Как уже
говорилось ранее, вид критической
области зависит от выбора конкурирующей
гипотезы. Разберем возможные случаи:
 .
В этом случае критическая область
ищется, как правосторонняя из условия
.
В этом случае критическая область
ищется, как правосторонняя из условия
 а
критическую точку ищут по таблицам
квантилей распределения2:
а
критическую точку ищут по таблицам
квантилей распределения2:
 После
этого вычисляем по данной выборке
наблюдаемое значение критерия. Если
После
этого вычисляем по данной выборке
наблюдаемое значение критерия. Если то нулевая гипотеза принимается.
то нулевая гипотеза принимается. .
В этом случае критическую область ищут
как левостороннюю. Критическая точка
ищется как
.
В этом случае критическую область ищут
как левостороннюю. Критическая точка
ищется как
 .
Тогда, если
.
Тогда, если ,
то нулевая гипотеза принимается.
,
то нулевая гипотеза принимается. .
В этом случае критическая область
ищется как двусторонняя. Критические
точки находятся из условий
.
В этом случае критическая область
ищется как двусторонняя. Критические
точки находятся из условий

 Им
соответствуют квантили порядка α/2 и
1-α/2 распределения «хи-квадрат» (таблица
5).
Им
соответствуют квантили порядка α/2 и
1-α/2 распределения «хи-квадрат» (таблица
5).
Пример.
При обработке
выборки объема n=20 получено
значение![]() .
Проверить гипотезу о том, что заданное
значение
.
Проверить гипотезу о том, что заданное
значение![]() равно
дисперсии случайной величины против
двусторонней конкурирующей гипотезы
на уровне значимости 10%.
равно
дисперсии случайной величины против
двусторонней конкурирующей гипотезы
на уровне значимости 10%.
Имеем:
![]() ;
;![]() ;
α=0,1; α/2=0,05; 1-α/2=0,95. По таблице 5 находим
;
α=0,1; α/2=0,05; 1-α/2=0,95. По таблице 5 находим![]() ;
;![]() .
Эти точки определяют границы двусторонней
критической области. Найдем наблюдаемое
значение критерия
.
Эти точки определяют границы двусторонней
критической области. Найдем наблюдаемое
значение критерия![]() .
Следовательно, принимается гипотеза
.
Следовательно, принимается гипотеза![]() .
.
§ 6.3. Проверка гипотезы о равенстве генеральной средней нормально распределенной генеральной совокупности некоторому значению
Пусть
известно, что генеральная совокупность
распределена нормально. Кроме этого
есть основания предполагать, что
генеральная средняя равна некоторому
значению a0. Тогда
выдвинем нулевую гипотезу![]() «генеральная
средняя данной генеральной совокупности
равна гипотетическому значению
«генеральная
средняя данной генеральной совокупности
равна гипотетическому значению![]() »,
причем известен второй параметр –
дисперсия
»,
причем известен второй параметр –
дисперсия![]() .
.
Возможны три случая
выдвижения альтернативной гипотезы:
![]() ;
;![]() ;
;![]() .
.
Для статистической
проверки нулевой гипотезы из генеральной
совокупности извлекают выборку объема
n. По ней рассчитываем
выборочное среднее![]() и при заданном уровне значимости
и при заданном уровне значимости![]() нужно оценить, значимо или незначимо
различаются
нужно оценить, значимо или незначимо
различаются![]() иa0. Это делается
следующим образом.
иa0. Это делается
следующим образом.
Для проверки
заданной нулевой гипотезы выберем
критерий случайную
величину с известным законом распределения:![]() ,
которая имеет нормальное распределение,
причем
,
которая имеет нормальное распределение,
причем![]() .
По этому критерию и уровню значимости
строится критическая область. Как уже
говорилось ранее, вид критической
области зависит от выбора конкурирующей
гипотезы. Разберем возможные случаи:
.
По этому критерию и уровню значимости
строится критическая область. Как уже
говорилось ранее, вид критической
области зависит от выбора конкурирующей
гипотезы. Разберем возможные случаи:
Если
 ,
то ищется двусторонняя критическая
область с симметричными относительно
нуля критическими точками, которые
определяются из условия
,
то ищется двусторонняя критическая
область с симметричными относительно
нуля критическими точками, которые
определяются из условия ,
где
,
где −
функция Лапласа, или из условия
−
функция Лапласа, или из условия ,
где
,
где − интегральная функция нормального
распределения. То есть,
− интегральная функция нормального
распределения. То есть, − это квантиль порядка
− это квантиль порядка нормального распределения.
нормального распределения.Если
 ,
то ищется правосторонняя критическая
область критической точкой, которая
определяются из условия
,
то ищется правосторонняя критическая
область критической точкой, которая
определяются из условия ,
где
,
где −
функция Лапласа, или из условия
−
функция Лапласа, или из условия ,
где
,
где − интегральная функция нормального
распределения. То есть,
− интегральная функция нормального
распределения. То есть, − это квантиль порядка
− это квантиль порядка нормального распределения.
нормального распределения.Если
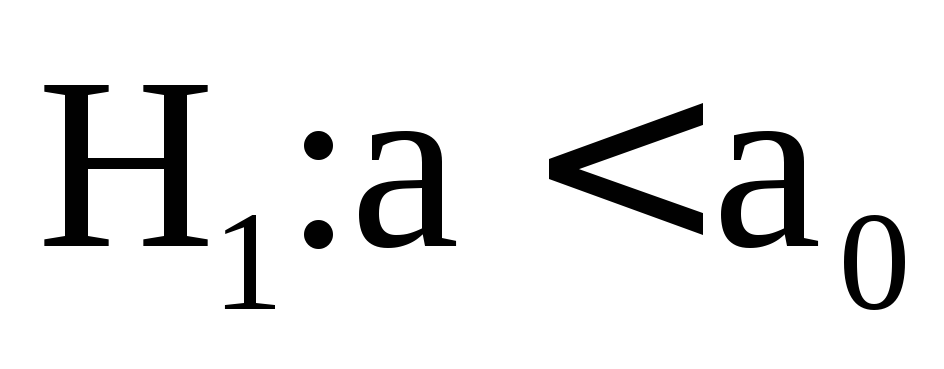 ,
то ищется левосторонняя критическая
область с критической точкой, которая
определяются из условия
,
то ищется левосторонняя критическая
область с критической точкой, которая
определяются из условия .
.
Если
второй параметр дисперсия
![]() неизвестен,
то для проверки заданной нулевой гипотезы
выберем критерийслучайную величину с известным законом
распределения:
неизвестен,
то для проверки заданной нулевой гипотезы
выберем критерийслучайную величину с известным законом
распределения:![]() ,
которая имеет распределение Стьюдента
сk=n-1
степенями свободы. По этому критерию и
уровню значимости строится критическая
область. Разберем возможные случаи:
,
которая имеет распределение Стьюдента
сk=n-1
степенями свободы. По этому критерию и
уровню значимости строится критическая
область. Разберем возможные случаи:
Если
 ,
то ищется двусторонняя критическая
область с симметричными относительно
нуля критическими точками, которые
определяются из условия
,
то ищется двусторонняя критическая
область с симметричными относительно
нуля критическими точками, которые
определяются из условия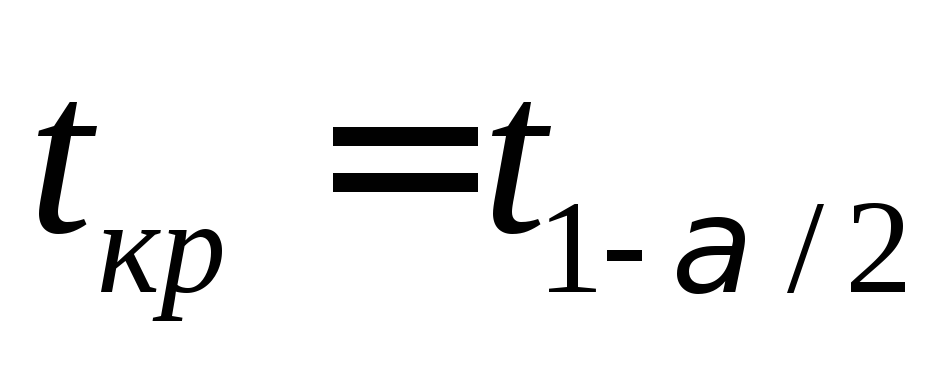 То есть,
То есть, − это квантиль порядка
− это квантиль порядка распределения Стьюдента.
распределения Стьюдента.Если
 ,
то ищется правосторонняя критическая
область критической точкой, которая
определяются из условия
,
то ищется правосторонняя критическая
область критической точкой, которая
определяются из условия .
То есть,
.
То есть, − это квантиль порядка
− это квантиль порядка распределения Стьюдента.
распределения Стьюдента.Если
 ,
то ищется левосторонняя критическая
область с критической точкой, которая
определяются из условия
,
то ищется левосторонняя критическая
область с критической точкой, которая
определяются из условия .
.
Примеры:
Проверить гипотезу о том, что заданное значение a=2 равно математическому ожиданию нормально распределенной случайной величины с известной дисперсией равной 9, против альтернативной двусторонней гипотезы на уровне значимости 5%, если в результате обработки выборки объема 10 получено значение средней равное 3.
Имеем
![]() ;
;![]() ;
α= 0,05;1-α/2=0,975. По
таблице 2 найдемz0,975квантиль порядка 0,975 стандартного
нормального распределения:z0,975=1,96.
Это критическая точка, определяет
симметричную относительно нуля
двустороннюю критическую область.
Найдем наблюдаемое значение критерия
;
α= 0,05;1-α/2=0,975. По
таблице 2 найдемz0,975квантиль порядка 0,975 стандартного
нормального распределения:z0,975=1,96.
Это критическая точка, определяет
симметричную относительно нуля
двустороннюю критическую область.
Найдем наблюдаемое значение критерия![]() .
.
Оно не попадает в критическую область.
Следовательно, принимается гипотеза![]() .
.
Проверить гипотезу о том, что заданное значение a=20 равно математическому ожиданию нормально распределенной случайной величины, против альтернативной правосторонней гипотезы на уровне значимости 5%, если в результате обработки выборки объема 10 получено значение средней равное 22 и исправленной дисперсией равной 4.
Имеем
![]() ;
;![]() ;
α= 0,05;1-α=0,95. По
таблице 3 найдемt0,95квантиль порядка 0,95 распределения
Стьюдентаcn-1=9
степенями свободы:t0,95(9)=1,833.
Это критическая точка, определяет
правостороннюю критическую область.
Найдем наблюдаемое значение критерия
;
α= 0,05;1-α=0,95. По
таблице 3 найдемt0,95квантиль порядка 0,95 распределения
Стьюдентаcn-1=9
степенями свободы:t0,95(9)=1,833.
Это критическая точка, определяет
правостороннюю критическую область.
Найдем наблюдаемое значение критерия![]() .
Это значение попадает в критическую
область, следовательно принимается
гипотеза
.
Это значение попадает в критическую
область, следовательно принимается
гипотеза![]() .
.
