ГОУ ВПО «Рязанский государственный медицинский университет

имени академика И.П. Павлова Федерального агентства по

здравоохранению и социальному развитию»

Кафедра математики и информатики

ПРИМЕРЫ ВЫПОЛНЕНИЯ, ВАРИАНТЫ ЗАДАНИЙ

Методические указания

Рязань 2007

УДК 512.8 (075.83)

ББК 22.11

К 651

Контрольные работы по математике и информатике: примеры выполнения, варианты заданий. /Сост. М.П. Булаев, И.С. Аверина. Рязань, РГМУ, 2007. – 100 с.

Рецензенты: В.В. Белов, доктор технических наук,

профессор Рязанской государственной

радиотехнической академии;

В.С. Богданов, кандидат технических наук,

доцент Рязанской государственной

радиотехнической академии.

Указания подготовлены в помощь студентам-заочникам специальности “фармация”, обучающимся на базе среднего специального образования с дифференцированным выбором вариантов заданий при выполнении контрольных работ по математике и информатике.

Табл: Ил.: Библиогр. 25 наз.

Печатается по решению Учебно-методического Совета Рязанского государственного медицинского университета им. акад. И.П. Павлова.

© Булаев М.П.

© РГМУ, 2007

Часть I математика Раздел 1. Дифференциальное исчисление

1.1 Определение производной. Таблица производных

Рассмотрим функцию y=f(x). Предположим, что x₀ внутренняя точка множества определения функции. Зададим приращение аргумента x0 такое, что точка x₀+xD_f. Тогда соответствующее приращение в т. x₀ будет иметь вид: f=f(x₀+x)–f(x₀).

Опр. Если существует предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента х0, то он называется значением производной функции f(x) в точке х₀

Обозначение: .

Таблица производных

1. С  = 0, где С–постоянная

2. (x^m) = mx^m–1

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

15. 

16. 

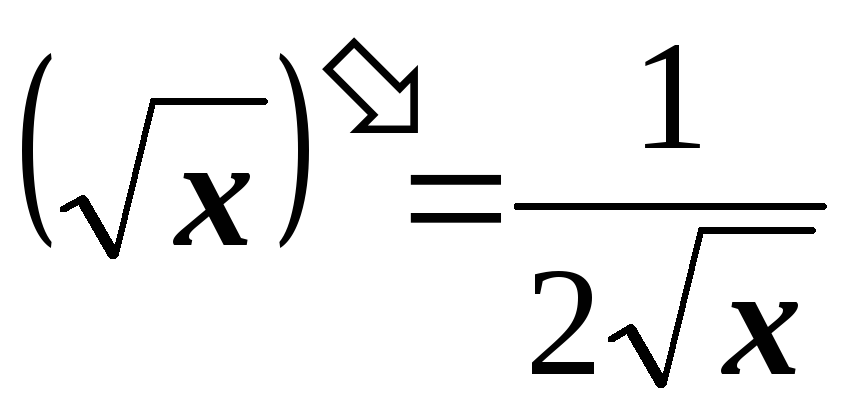
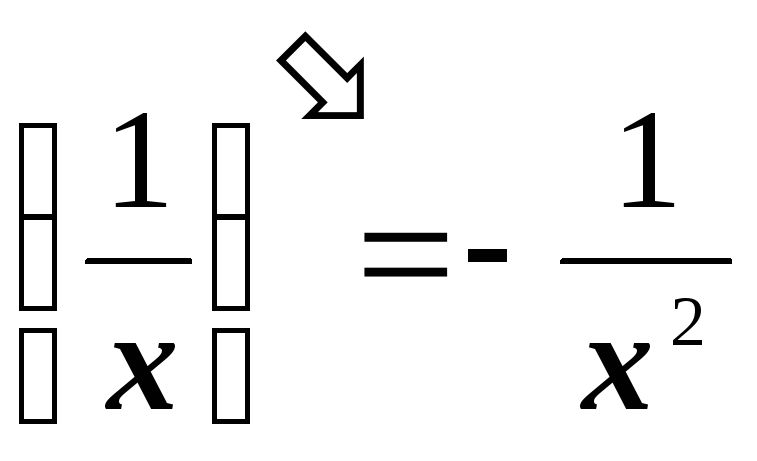
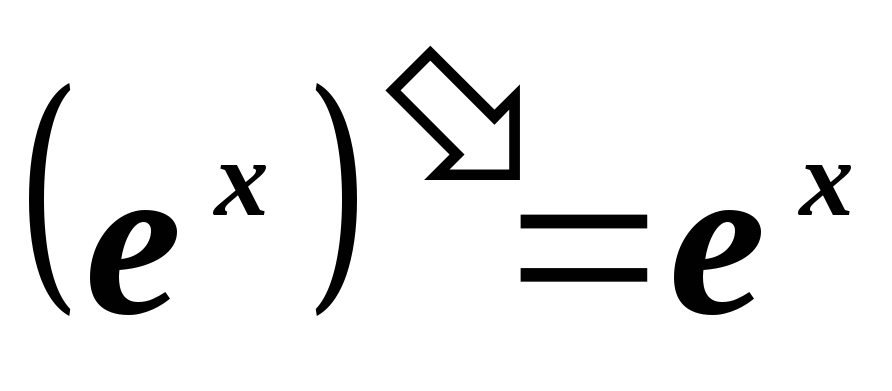
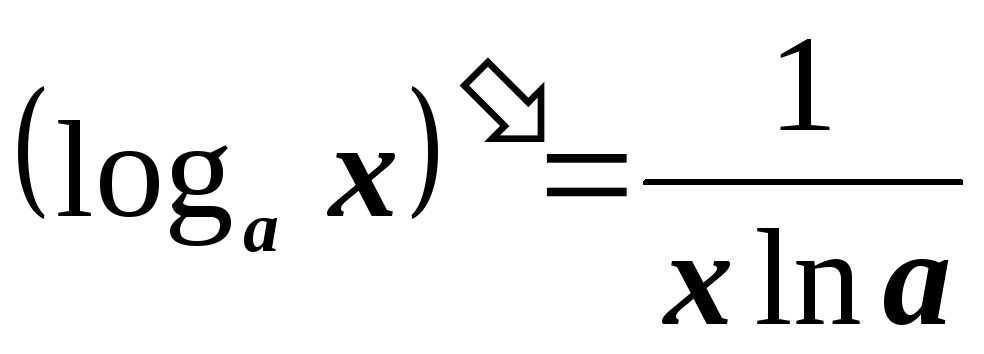
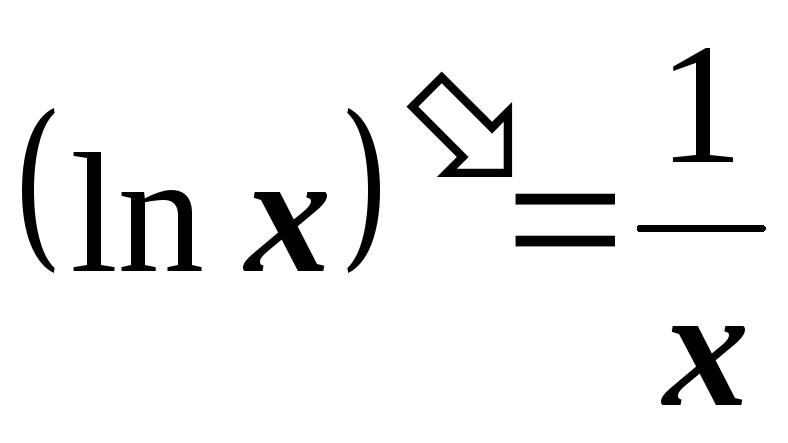
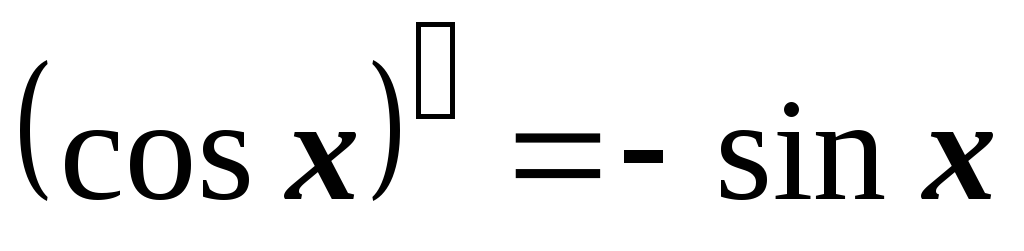
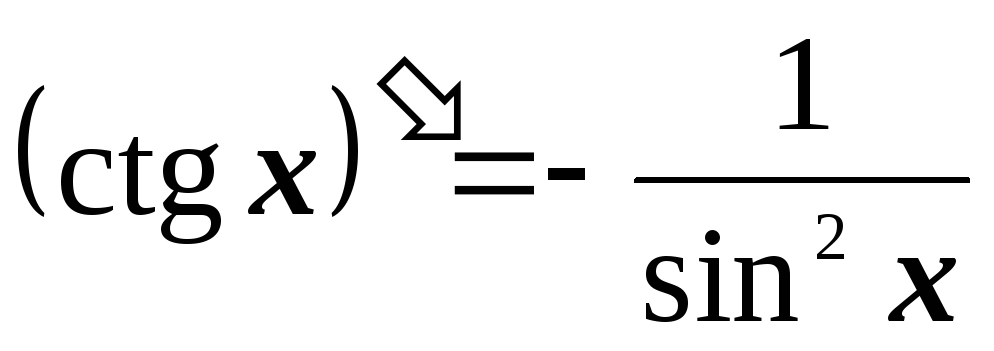
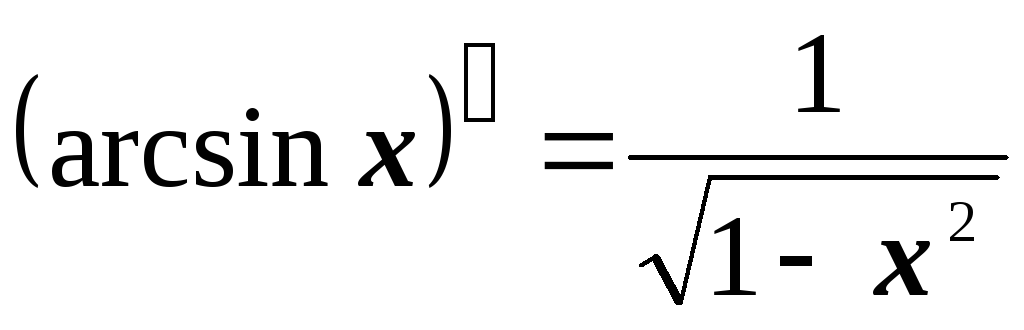
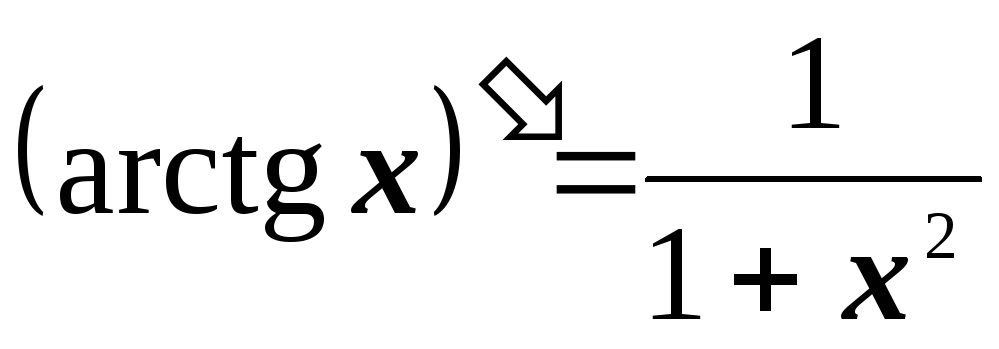
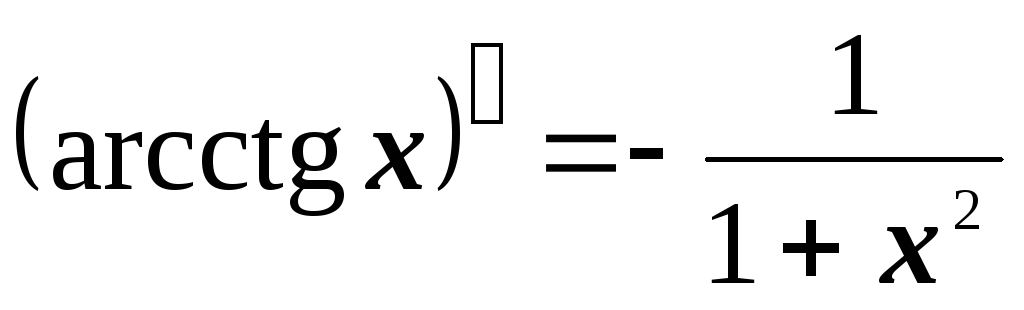
1.2. Основные правила дифференцирования

Пусть u и v – функции, дифференцируемые в точке х. Тогда

1. Производная суммы двух дифференцируемых функций равна сумме их производных:

(u+v) ′=u′+v′

2. Производная произведения двух дифференцируемых функций вычисляется по следующему правилу: (uv) ′=u′v+uv′, в частности (Cu) ′=Cu′, С=const (постоянный множитель можно выносить за знак производной)

3. Производная частного двух дифференцируемых функций вычисляется по следующему правилу:

, где v  0

4. Производная сложной функции равна производной по промежуточному аргументу, умноженной на производную промежуточного аргумента по независимой переменной: y′_x=y′_{u ·} u′_x, где и – промежуточный аргумент.

1.3. Численное дифференцирование

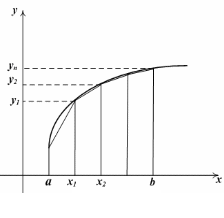
При анализе медицинских, инженерных и научных данных часто возникает необходимость найти наклон кривой, которая задана таблицей значений.

Возможна и другая ситуация: f(x) известна, но имеет очень сложное аналитическое выражение.

В первом случае классические методы дифференциального исчисления просто неприемлемы, а во втором случае их использование вызывает значительные трудности. В таких задачах вместо функции f(x) рассматривают интерполирующую функцию P(x), а затем полагают f '(x)  P'(x) на интервале axb. Аналогично поступают при нахождении производных высших порядков функции f(x).

Если для интерполирующей функции P(x) известна погрешность интерполяции R(x)=f(x)–P(x), то погрешность производной равна производной от погрешности этой функции

r(x)=f '(x)–P'(x)=R'(x).

Такое утверждение справедливо и для производных высших порядков.

В целом же численное дифференцирование представляет собой операцию менее точную, чем интерполирование.

Формулы для вычисления первой производной

Численное дифференцирование весьма чувствительно к погрешностям, вызванным неточностью исходных данных. Значительно меньшую погрешность имеет дифференцирование многочленов наилучшего среднеквадратического приближения (методом наименьших квадратов). На практике часто применяются формулы безразностного дифференцирования для производной первого порядка:

По трем точкам:

(1.3.1)

По четырем точкам:

; (1.3.2)

;

.

По пяти точкам:

;

;

; (1.3.3)

;

.

Формулы второй производной

По четырем точкам:

; (первое значение)

; (внутренние точки) (1.3.4)

. (последнее значение)

По пяти точкам:

;

;

; (1.3.5)

;

.

Заметим, что с ростом порядка производной резко падает точность численного дифференцирования. Поэтому на практике редко применяют формулы для производных второго порядка.