2.5. Основные понятия и свойства определенного интеграла

Пусть функция f(x) определена на отрезке [a; b]. Разобьем отрезок [a; b] на n частей точками a=x₀<x₁<…<x_n–1<x_n=b; на каждом элементарном отрезке [x_k–1, x_k] выберем произвольную точку c_k и обозначим через длину каждого такого отрезка. Вычислим значения функции f(x) в точках c_k, где k={1, 2, …, n}.

Опр. Интегральной суммой для функции f(x) на отрезке [a; b] называется сумма вида

(2.5.1)

Опр. Определенным интегралом от функции f(x) на отрезке [a; b] называется предел интегральной суммы (2.5.1), при условии, что длина наибольшего из элементарных отрезков стремится к нулю:

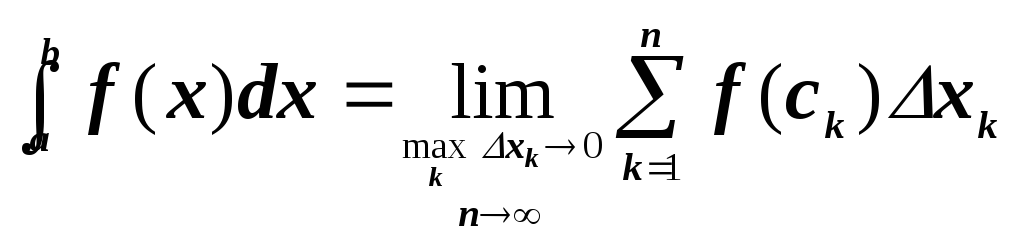(2.5.2)

При этом f(x) называется подынтегральной функцией, x – переменной интегрирования, числа а и b – соответственно нижним и верхним пределами интегрирования, [a; b] – промежутком интегрирования.

Простейшие свойства определенного интеграла

1. Определенный интеграл не зависит от обозначения переменной интегрирования, т.е.

2. 

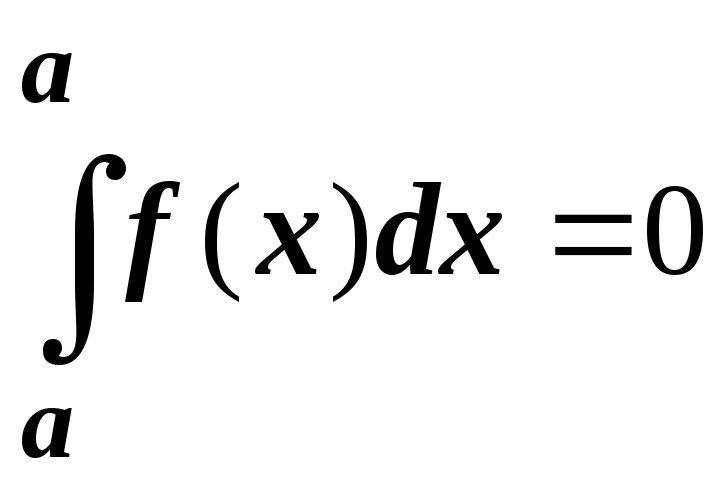
3. Определенный интеграл от суммы конечного числа непрерывных функций f₁(x), f₂(x), …, f_n(x), заданных на отрезке [a; b], равен сумме определенных интегралов от этих функций:

4. Постоянный множитель можно выносить за знак определенного интеграла:

5. 

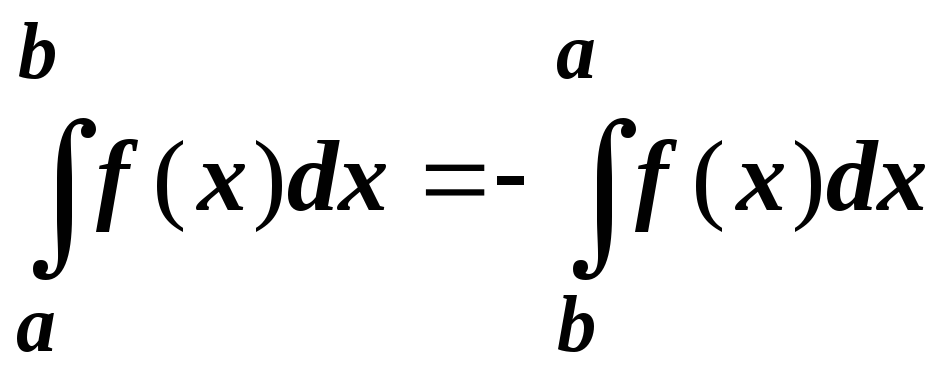
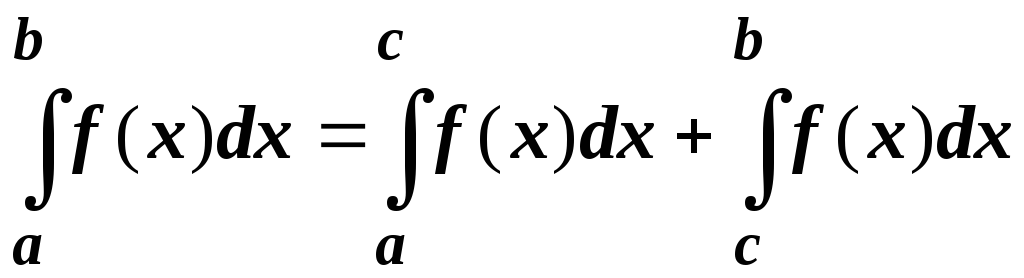6. , где a < c < b.

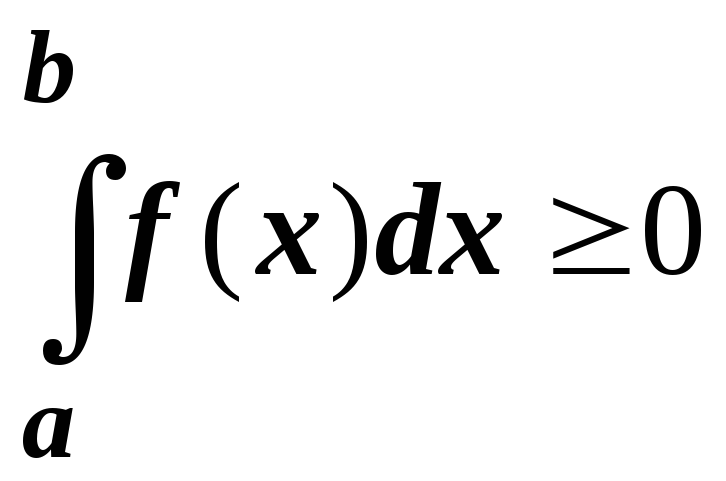7. Если f(x)0 на отрезке [a; b], то ; если f(x)0 на отрезке [a; b], то .

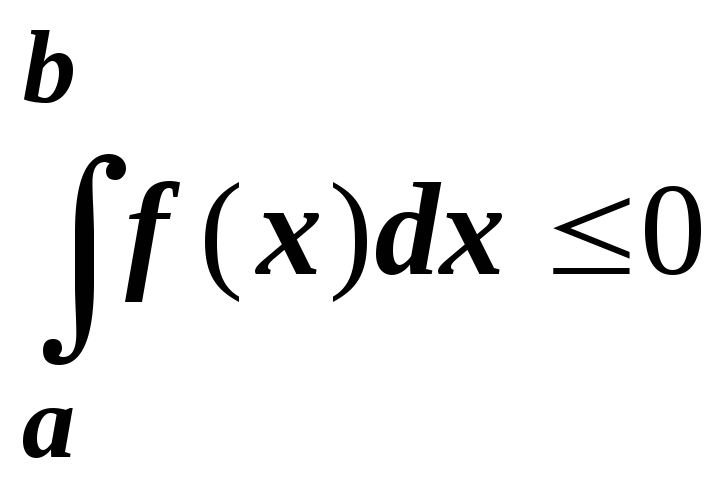2.6. Основные методы интегрирования

1) Формула Ньютона-Лейбница. Для вычисления определенного интеграла от непрерывной на отрезке [a;b] функции f(x) в том случае, когда может быть найдена ее первообразная F(x) служит формула Ньютона-Лейбница:

,

т.е. определенный интеграл равен разности значений любой первообразной при верхнем и нижнем пределах интегрирования.

2) Метод подстановки. При вычислении определенного интеграла методом замены переменной (метод подстановки) данный интеграл преобразуется с помощью подстановки t=(x) или x=(t) в определенный интеграл относительно новой переменной интегрирования t. При этом старые пределы интегрирования a, b заменяются новыми переделами интегрирования  и  соответственно, которые находятся из исходной подстановки.

Из первой подстановки новые пределы интегрирования вычисляются непосредственно: =(a), =(b). Из второй подстановки новые пределы интегрирования находятся путем решения уравнений ()=a, ()=b относительно  и .

Таким образом, имеем

Здесь предполагается, что функции (t) и ΄(t) непрерывны на отрезке [; ], а функция f((t)) определена и непрерывна на отрезке  t  .

3) Интегрирование по частям. Если функции u=u(x) и v=v(x) имеют непрерывные производные на отрезке [a; b], то для вычисления определенного интеграла используют формулу , которая называется формулой интегрирования по частям для определенного интеграла.

2.7. Численное интегрирование

Существует огромное количество функций, интеграл от которых не может быть выражен через элементарные функции. Для нахождения интегралов от подобных функций применяются разнообразные приближенные методы, суть которых заключается в том, что подынтегральная функция заменяется «близкой» к ней функцией, интеграл от которой выражается через элементарные функции.

Формула прямоугольников

Если известны значения функции f(x) в некоторых точках x₀, x₁, … , x_m, то в качестве функции «близкой» к f(x) можно взять многочлен Р(х) степени не выше m, значения которого в выбранных точках равны значениям функции f(x) в этих точках.

Разобьем отрезок интегрирования [a; b] на n равных частей. Обозначим длину каждой части. При этом y₀ = f(x₀), y₁ = f(x₁), …., y_n = f(x_n).

Составим суммы: y₀x + y₁x + … + y_n-1x

y₁x + y₂x + … + y_nx

Это соответственно нижняя и верхняя интегральные суммы. Первая соответствует вписанной ломаной, вторая – описанной.

Тогда

или (2.7.1)

любая из этих формул может применяться для приближенного вычисления определенного интеграла и называется общей формулой прямоугольников.

Формула трапеций

Эта формула является более точной по сравнению с формулой прямоугольников. Подынтегральная функция в этом случае заменяется на вписанную ломаную.

Геометрически площадь криволинейной трапеции заменяется суммой площадей вписанных трапеций (рис. 2.7.1). Очевидно, что чем больше взять точек n разбиения интервала, тем с большей точностью будет вычислен интеграл.

Площади вписанных трапеций вычисляются по формулам:

После приведения подобных слагаемых получаем формулу трапеций:

(2.7.2)

Формула Симпсона

(формула парабол или квадратурная формула)

Разделим отрезок интегрирования [a, b] на четное число отрезков п=2m.

Формула Симпсона имеет вид:

Чем больше взять число m, тем более точное значение интеграла будет получено.