3.4 Другие числовые характеристики дискретной случайной величины

3.4.1 Среднеквадратическое отклонение

Среднеквадратическим отклонением случайной величины X называется квадратный корень из ее дисперсии

(X)=(D(X))^0.5

В отличие от дисперсии, размерность которой соответствует квадрату размерности случайной величины, среднеквадратичное отклонение измеряется в тех же единицах, что и сама случайная величина X и является более наглядной характеристикой степени разброса значений.

3.4.2. Моменты k-го порядка

Начальным моментом k-го порядка случайной величины X называется математическое ожидание величины X^k

_k (X)=M(X ^k)=p_ix_i^k

ⁱ

Таким образом, математическое ожидание случайной величины является ее начальным моментом первого порядка. Моменты с k1 позволяют “усилить ” роль тех значений, которые имеют малую вероятность, но большую величину.

Разность между случайной величиной X и ее математическим ожиданием называется центрированной случайной величиной.

_

X= X -M(X)

Центральным моментом k-го порядка случайной величины X называется математическое ожидание k-ой степени соответствующей центрированной величины.

_

M_k(X)=M(X ^k)=p_i(x_i- M(X))^k

ⁱ

Дисперсия случайной величины является ее вторым центральным моментом.

3.4.3. Нормированная случайная величина

Нормированной случайной величиной называется величина

_

X=X/(X)

Легко показать, что

_

D(X)=D(X/(X))=1/((X)²D(X)=1

3.4.4. Функция распределения дискретной случайной величины.

Функция распределения дискретной случайной величины равна вероятности того, что дискретная случайная величина X в результате испытания примет значение, меньшее, чем заданная величина x.

F(x)=P(Xx), 0 F(x)1, -x

Рассмотрим в качестве примера дискретную случайную величину

xi	1	4	8
pi	0.3	0.1	0.6

X

При x1 функция F(x)=P(X x)=0

При 1x4 функция F(x)=P(X x)=0.3

При 4x8 функция F(x)=P(X x)=0.3+0.1=0.5

При x8 F(x)=P(X x)=1

На графике эта функция будет выглядеть следующим образом:

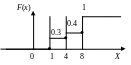
Рис. 7. Пример функции распределения дискретной случайной величины

3.4.5. Мода и медиана дискретной случайной величины

Модой дискретной случайной величины является ее наиболее вероятное значение. Например, в случае биномиального закона распределения наиболее вероятным будет значение k₀=[np-q]+1. В примере, рассмотренном выше - Mo= 8.

Медиана дискретной случаной величины равна значению, начиная с которого функция распределения превышает 0.5. В рассмотренном примере Me=8

3.4.6. Ковариация и коэффициент корреляции

Пусть X и Y -две дискретные случайные величины с законами распределения

xk	x1	x2	...	xm
pk	p1	p2	...	pm

X

и

yi	y1	y2	...	yn
pi	g1	g2	...	gn

Y

Пусть для этих величин математическое ожидание равно M(X) и M(Y), а дисперсия - D(X) и D(Y). В общем случае эти величины могут быть зависимыми и математическое ожидание для произведения величин X и Y должно вычисляться по формуле

M(XY)=p_ijx_iy_j,

^ij

В данном выражении p_ij - вероятность того, что величины X и Y одновременно примут значения x_i и y_j. Для независимых случайных величин

p_ij= p_i g_j

Ковариацией случайных величин X и Y называют математическое ожидание произведения центрированных случайных величин

_{ }

Cov(X, Y)=M(XY)=M([X-M(X)][Y-M(Y)])

Для дискретных случайных величин X и Y

_{ }

Cov(X, Y)=M(XY)= p_ij[x_i- M(X)][y_j- M(Y)]

^ij

Если в определении ковариации раскрыть скобки, получим:

Cov(X, Y)= M([X-M(X)][Y-M(Y)])=

=M([XY-M(X)Y-M(Y)X+M(X)M(Y)]=

= M(XY)-2 M(X)M(Y)+M(X)M(Y)=

== M(XY)-M(X)M(Y)

Таким образом, мы получили для ковариации выражение, уже использованное ранее при доказательстве формулы для дисперсии суммы двух случайных величин. Как уже отмечалось, в случае, если X и Y - независимые величины, то Cov(X, Y)= 0.

Ковариация нормированных случайных величин

_{ }

X=X/(X) и Y=Y/(Y)

называется коэффициентом корреляции.

_{ }

( X, Y)= Cov(X, Y)=Cov(X, Y)/(X)/(Y)

Так же, как и ковариация, коэффициент корреляции обращается в 0, если величины X и Y независимы. Вместе с тем, обратное верно не всегда, то есть и для зависимых величин возможна ситуация, когда коэффициент корреляции равен 0.

Сверху значения модуля коэффициента корреляции ограничены единицей

|(X, Y)|1

Рассмотрим выражение

_{     }

D(X + Y)= D(X)+ D(Y)+2 Cov(X, Y)=2[1⁺(X, Y)]0

Дисперсия не может быть отрицательной, поскольку в нее входят квадраты отклонений и неотрицательные вероятности. Для того, чтобы это условие было выполнено, необходимо, чтобы заключительное выражение в скобках было неотрицательным, то есть коэффициент корреляции обязан быть по модулю не больше единицы.

Равенство коэффициента корреляции единице выполняется только в том случае, когда величины X и Y связаны между собой линейной зависимостью

Пусть

|(X, Y)|=1

Тогда

_{ }

D(X ⁺ Y)= 0,

следовательно

_{ }

X ⁺ Y=C= const,

и

_{ }

Y= C ⁺X, Y= C ⁺(Y)/(X)X,

то есть величины связаны линейно.

С другой стороны, если величины связаны линейной зависимостью

Y= aX+b,

то

M(Y)=aM(X)+b, D(Y)=a²D(X),

M(XY)= M(X(aX+b))= aM(X²)+bM(X)

M(X)M(Y)= a(M(X))²+bM(X)

и

_{ }

( X, Y)= Cov(X, Y)=Cov(X, Y)/(X)/(Y)=

=[M(XY)- M(X)M(Y)]/(X)/(Y)= a·D(X)/((X)(X)|a|)

Результат равен 1 при a 0 и –1 при a 0