5.3.3. Мода и медиана

Модой непрерывной случайной величины X называют такое значение x_Mo=x₀, для которого функция плотности распределения f(x₀) максимальна.

Медианой непрерывной случайной величины X называют такое значение x_Me=x₀, для которого функция распределения равна 0.5

P(X x_Me)= P(X x_Me)= F(x_Me)=0.5

5.3.4. Моменты k-го порядка

Начальным моментом k-го порядка непрерывной случайной величины X называется математическое ожидание величины величины X^k

_

_k (X)=M(X ^k)= ∫x^k f(x)dx

^-

Центральным моментом k-го порядка непрерывной случайной величины X называется математическое ожидание k-ой степени соответствующей центрированной величины.

_{ }

M_k(X)=M(X ^k)= ∫[x-M(X)]^kf(x)dx

^-

5.3.5. Асимметрия и эксцесс.

Для характеристики общего вида графика плотности вероятности случайной величины вводят такие параметры, как асимметрия и эксцесс.

Для оценки асимметрии распределения случайной величины можно использовать любой нечетный центральный момент, если его порядок выше первого. Обычно используется нормированный третий момент случайной величины

as=³/³=1/³M([X-M(X)]³)

При as0 асимметрия положительна и более длинное крыло кривой распологается справа от математического ожидания. При as0 асимметрия отрицательна и «длинна часть» кривой распологается слева от математического ожидания. Для симметричного распределения as=0.

Эксцесс теоретического распределения вводится как

Ek=⁴/⁴-3.

Если случайная величина распределена в соответствии с нормальным законом, Ek=0. При Ek0 – функция плотности распределения имеет более низкую и плоскую вершину, чем в случае нормального распределения, при Ek0 – более высокую и острую вершину.

5.3. Законы распределения непрерывной случайной величины

5.3.1. Равномерное распределение

Распределение называется равномерным, если плотность вероятности постоянна на интервале axb и равна 0 вне интервала.

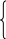
0, xa

f(x)= 1/(b-a), axb

1, xb

f(x) 1/(b-a)

0 a b x

Рис. 8. Равномерное распределение (плотность распределения)

Пользуясь свойствами функции распределения легко показать, что

При xa функция

_x

F(x)= P(-X x)= ∫ f(t)dt=0

^-

При axb функция

_{0 x}

F(x)=P(-Xx)= ∫ f(t)dt + ∫ f(t)dt=x/(b-a)

^{- a}

При xb F(x)=P(-X x)=1

_{0 b x b}

F(x)=P(-Xx)= ∫ f(t)dt + ∫ f(t)dt +∫ f(t)dt =∫1/(b-a)dx=(b-a)/(b-a)=1

^{- a b a}

Таким образом,

0, xa

F(x)= (x-a)/(b-a), axb

1, xb

F(x) 1

x/(b-a)

0 a b x

Рис. 9. Равномерное распределение (функция распределения)

Математическое ожидание для равномерного распределения

_{b b b}

M(x)= ∫ xf(x)dx=∫1/(b-a) xdx=1/2x²/(b-a)=(b²- a²)/(b-a)/2=(a+b)/2

^{a a a}

Дисперсия равномерного распределения

_b

D(X)=M([X]²)-[M(X)]²=∫x²/(b-a)dx-[(b+a)/2]²=(b-a)²/12

^a

Мода для равномерного распределения не существует, медиана x_Me==(a+b)/2.