2.2.3. Скорости и ускорения точек твердого тела, вращающегося вокруг неподвижной оси

С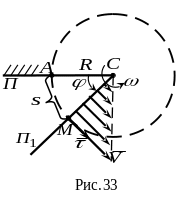 корости и ускорения точек вращающегося твердого тела определяются кинематическими характеристиками движения тела в целом и положением точек в теле.

При вращении тела вокруг неподвижной оси все его точки описывают окружности, плоскости которых перпендикулярны этой оси, а центры лежат на ней. Рассмотрим точку тела (рис. 32), лежащую в полуплоскости и находящуюся от оси вращения на расстоянии ; ее траектория – окружность радиуса с центром . Покажем вид на траекторию точки тела с положительного конца оси (рис. 33).

Применим естественный способ задания движения точки. За начало отсчета дуговой координаты выберем точку , лежащую в неподвижной полуплоскости . Положительное направление отсчета соответствует положительному направлению отсчета угла поворота .

Положение точки в данный момент времени определяется соотношением , где значение выражено в радианах.

Итак, уравнение движения точки по траектории имеет вид

. (88)

Проекция скорости на касательную в соответствии с (51), получается путем дифференцирования (87) по времени

. (89)

Вектор скорости направлен в сторону вращения тела по касательной к окружности и, следовательно, перпендикулярен к радиусу описываемой окружности (рис.33).

Модуль скорости точки равен

. (90)

Модули скоростей точек вращающегося тела пропорциональны «радиусам точек», т. е. расстояниям этих точек до оси вращения.

Эпюра векторов скоростей точек, лежащих на радиусе представлена на рис. 33.

Проекция ускорения точки на касательную в соответствии с (71)

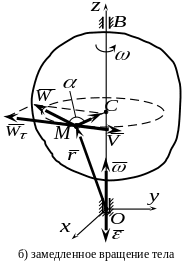. (91)

Модуль касательного ускорения равен

. (92)

Модуль нормального ускорения точки равен , но , а для окружности ; следовательно, имеем:

. (93)

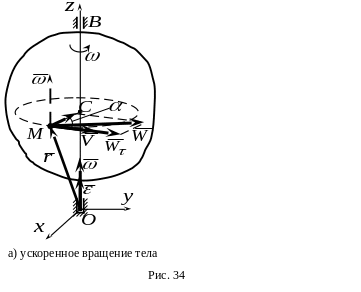
Рассмотрим твердое тело, вращающееся вокруг неподвижной оси (рис 34).

Касательное ускорение точки направлено по касательной в сторону вращения тела (рис. 34а), если вращение ускоренное, и в сторону, противоположную вращению тела, (рис.34б), если вращение замедленное.

Нормальное ускорение точки всегда направлено от точки к оси вращения тела (к центру описываемой точкой окружности).

Модули ускорений и пропорциональны расстояниям точек вращающегося тела до оси вращения.

Полное ускорение точки в соответствии с (70) равно , а его модуль равен:

(94)

Направление вектора полного ускорения точки определяется углом , образуемым вектором с радиусом . Из рис.34 видно, что:

. (95)

В частном случае равномерного вращения тела имеем:

, .

Полное ускорение направлено по радиусу к оси вращения от точки .

2.2.4. Векторные формулы для кинематических характеристик вращающегося твердого тела

Угловую скорость и угловое ускорение можно рассматривать как векторы и , направленные вдоль оси вращения тела (рис.34). Проекции векторов и на ось равны

. (96)

Модули этих векторов представлены формулами (82), (87).

При ускоренном вращении векторы и направлены в одну сторону (рис. 34а); при замедленном - направления этих векторов противоположны (рис. 34б). В соответствии с первой формулой (96) вектор направлен по оси вращения в ту сторону, откуда вращение тела представляется происходящим в направлении против хода часовой стрелки.

Векторы и связаны зависимостью:

. (97)

Рассмотрим вновь твердое тело, вращающееся вокруг неподвижной оси (рис. 34). Выберем произвольную точку тела, находящуюся на расстоянии от оси вращения. Изобразим векторы скорости , касательного, нормального и полного ускорения , выберем произвольную точку на оси вращения и проведем из нее радиус-вектор точки . Докажем, что

. (98)

Модуль скорости равен , а модуль векторного произведения - .

Из треугольника видно, что , поэтому .

Вектор направлен перпендикулярно плоскости треугольника , содержащего перемножаемые векторы и . Вектор также направлен перпендикулярно к этой плоскости в ту сторону, откуда поворот вектора к вектору на наименьший угол между ними виден происходящим в направлении против хода часовой стрелки. Следовательно, векторы и направлены одинаково. Формула (98) тем самым доказана.

Используя формулу (41) для вектора скорости точки , можно написать

. (99)

Производная по времени от постоянного по модулю радиус-вектора, неизменно связанного с вращающимся твердым телом, равна векторному произведению угловой скорости его вращения вокруг оси на радиус-вектор.

Для вывода векторной формулы ускорения точки продифференцируем обе части равенства (98) по времени:

.

Здесь . Поэтому

. (100)

С другой стороны

.

Докажем, что

. (101)

По модулю касательное ускорение равно:

.

Легко доказать, что по направлению векторы и совпадают [смотри доказательство равенства (98)].

Докажем, что

. (101а)

По модулю нормальное ускорение равно :

, .

Но , поскольку ; следовательно .

Вектор направлен перпендикулярно плоскости, содержащей векторы и , по отрезку к точке [вектор мысленно перенесем в точку (рис. 34а)].