3.2.2. Пример решения задачи на свободные колебания точки
Пример
3. Гиря
массой
подвешена к пружине, коэффициент
жесткости которой
.
В начальный момент гиря была прикреплена
к нижнему концу недеформированной
пружины и отпущена без начальной
скорости. Пренебрегая массой пружины
и силами сопротивления, определить
закон движения гири, а также период и
амплитуду ее колебаний.
Решение.
Примем гирю
за материальную точку
,
движущуюся прямолинейно и вертикально,
к которой приложены сила тяжести
и сила упругости
(рис. 6). Совместим ось
с вертикальной траекторией точки
и рассмотрим три положения гири на этой
оси. На рисунке 6:
- положение нижнего конца недеформированной
пружины длиной
;
- положение равновесия гири, висящей на
пружине;
- текущее положение гири, фиксируемое
координатой
.
В положении статического равновесия гири будет выполняться условие
,
или
,
(а)
где
- статическая деформация пружины;
- статическая сила упругости пружины.
Начало отсчета координаты выберем в положении равновесия гири. Выведенная из положения равновесия гиря приходит в колебательное движение около положения равновесия.
Составим дифференциальное уравнение движения гири в проекции на ось :
;
(б)
и
учтем, что в момент времени
,
когда положение точки
определяется координатой
,
деформация пружины равна
,
а модуль силы упругости будет равен
.
Тогда c учетом уравнения (а) уравнение (б) примет вид:
,
или
, (в)
где .
Следовательно, точка совершает свободные гармонические колебания. Общее решение уравнения (в) представим как
. (г)
Из условий задачи находим начальные условия движения:
при
Собственная частота равна
,
начальное значение координаты
.
Окончательно закон движения гири запишется в виде:
.
Период свободных колебаний гири
.
Амплитуда свободных колебаний гири
.
3.2.2. Свободные затухающие колебания материальной точки
Свободные гармонические колебания в реальных условиях не реализуются, так как, кроме восстанавливающей силы, на тело действуют еще силы сопротивления. При небольших скоростях движения силу сопротивления можно считать пропорциональной первой степени скорости.
Рассмотрим
прямолинейное движение материальной
точки
под действием восстанавливающей силы
и силы сопротивления
,
равной
,
(27)
где
- постоянный положительный коэффициент,
а вектор силы
всегда направлен противоположно вектору
скорости
.
С
оставим
дифференциальное уравнение движения
точки в проекции на ось
(рис. 7):
.
(28)
Разделив уравнение (28) на и введя, кроме ранее принятого обозначения
, еще одно
,
(29)
приведем уравнение (28) к виду
.
(30)
Это уравнение представляет собой дифференциальное уравнение свободных затухающих колебаний материальной точки.
Из
теории линейных дифференциальных
уравнений известно, что при
общее решение уравнения (30)будет иметь
вид:
,
(31)
где
и
- постоянные интегрирования, зависящие
от начальных условий и равные соответственно
;
.
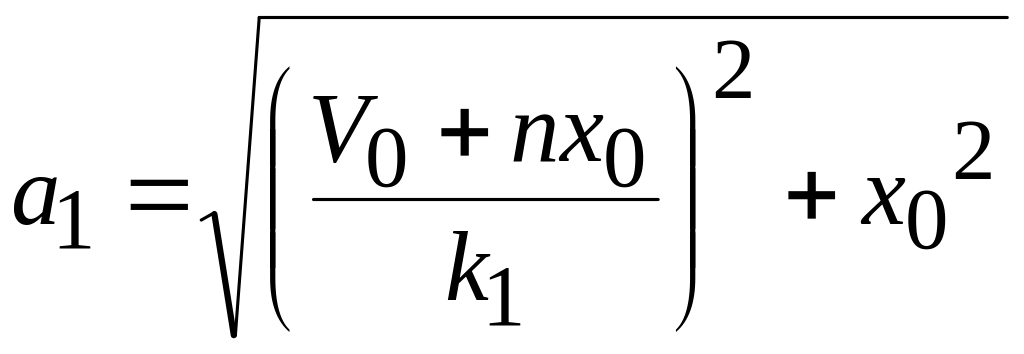(32)
Здесь
.
(33)
Постоянная
называется угловой частотой свободных
затухающих колебаний точки.
Н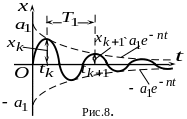
а
рис. 8 представлен график функции (31). Из
графика следует, что материальная точка,
выведенная из состояния равновесия и
находящаяся под действием восстанавливающей
силы и силы сопротивления, совершает
колебания, при которых наибольшие
отклонения точки от положения равновесия
с течением времени убывают.
Такие колебания называются затухающими.
Периодом
свободных затухающих колебаний называется
промежуток времени, в течение которого
два последовательных отклонения точки
от положения равновесия в одну и ту же
сторону достигают наибольшего значения.
Величина определяется соотношением:
.
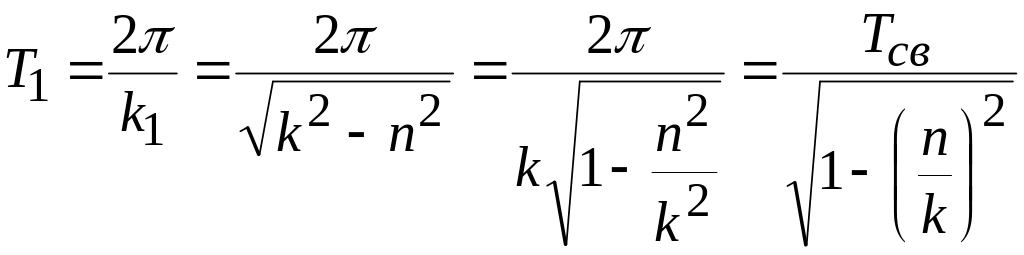(34)
Период
всегда несколько больше периода свободных
гармонических колебаний; однако это
превышение при малых сопротивлениях,
когда
мало, незначительно.
Свободные
затухающие колебания не являются
гармоническими, так как гармонические
колебания характеризуются неизменной
амплитудой. Решение (31) описывает
колебания с постоянной частотой
,
но с переменными отклонениями от
положения равновесия
,
которые при
стремятся к нулю.
Из
уравнения (31) также следует, что отношение
двух последовательных отклонений точки
и
,
соответствующих моментам времени
и
и отличающихся друг от друга на период
,
является постоянной величиной
.
(35)
Иными
словами, через равные промежутки времени
отклонения точки от положения равновесия
убывают по закону геометрической
прогрессии, при этом число
называется декрементом
затухающих колебаний.
Натуральный логарифм декремента
(36)
называется логарифмическим декрементом.