
- •Кафедра теоретической и прикладной механики теоретическая механика Учебно-методический комплекс
- •1. Информация о дисциплине
- •1.1. Предисловие
- •1.2. Содержание дисциплины и виды учебной работы
- •1.2.1. Содержание дисциплины по гос
- •1.2.2. Объем дисциплины и виды учебной работы
- •Раздел I. Статика (40 часов)
- •1.2. Моменты силы. Пара сил (10 часов)
- •1.3. Произвольная система сил (10 часов)
- •1.4. Плоская система сил (10 часов)
- •Раздел 2. Кинематика (60 часов)
- •2.1. Кинематика точки (13 часов)
- •2.2. Простейшие движения твердого тела (9 часов)
- •2.3. Сложное движение точки (15 часов)
- •2.4. Плоское движение твердого тела (15 часов)
- •2.5. Сферическое движение твердого тела. Общий случай движения свободного твердого тела (8 часов)
- •Раздел 3. Динамика (100 часов)
- •3.1. Дифференциальные уравнения движения материальной точки (10 часов)
- •3.2. Прямолинейные колебания материальной точки (12 часов)
- •3.3. Введение в динамику механической системы. Теорема об изменении количества движения системы и о движении центра масс системы (8 часов)
- •3.4. Теорема об изменении кинетического момента системы относительно неподвижных центра и осей (10 часов)
- •3.5. Теорема об изменении кинетической энергии системы (10 часов)
- •3.6. Динамика плоского движения твердого тела (10 часов)
- •3.7. Основы кинетостатики (10 часов)
- •3.8. Введение в аналитическую механику (8 часов)
- •3.9. Принцип возможных перемещений (11 часов)
- •3.10. Общее уравнение динамики. Уравнения Лагранжа второго рода (11 часов)
- •3.11. Элементарная теория гироскопа (13 часов)
- •3.12. Основы теории удара (17 часов)
- •Заключение
- •2.2. Тематический план дисциплины
- •2.2.1. Тематический план дисциплины для студентов очной формы обучения
- •2.2.2. Тематический план дисциплины для студентов очно-заочной формы обучения
- •2.2.3. Тематический план дисциплины для студентов заочной формы обучения
- •2.2.4. Тематический план дисциплины для студентов очной формы обучения
- •2.2.5. Тематический план дисциплины для студентов очно-заочной формы обучения
- •2.2.6. Тематический план дисциплины для студентов заочной формы обучения
- •2.4.1.2. Практические занятия (очно-заочная форма обучения)
- •2.4.1.3. Практические занятия (заочная форма обучения)
- •2.4.2. Практические занятия
- •2.4.2.2. Практические занятия (очно-заочная форма обучения)
- •2.4.2.3. Практические занятия (заочная форма обучения)
- •2.5. Временной график изучения дисциплины
- •2.5.1. Временной график изучения дисциплины «Теоретическая механика»
- •2.5.2. Временной график изучения дисциплины «Теоретическая механика»
- •2.6. Балльно-рейтинговая система оценки знаний
- •3. Информационные ресурсы дисциплины
- •3.1. Библиографический список
- •3.2. Опорный конспект по дисциплине Введение
- •Раздел 1. Статика
- •1.1. Введение в механику
- •1.1.1. Некоторые основные понятия и определения
- •1.1.2. Основные законы механики
- •1.1.3. Свободные и несвободные тела. Связи и реакции связей
- •1.2. Моменты силы. Пара сил
- •1.2.1.Предмет статики
- •1.2.2. Условия и уравнения равновесия материальной точки
- •1.2.3. Момент силы относительно точки
- •1.2.4. Момент силы относительно оси
- •1.2.5. Пара сил и ее свойства
- •1.3. Произвольная система сил
- •1.3.1. Приведение силы к данному центру
- •1.3.2. Основная теорема статики
- •1.3.3. Определение модулей и направлений главного вектора и главного момента
- •1.3.4. Уравнения равновесия произвольной системы сил.
- •1.4. Плоская система сил
- •1.4.1. Уравнения равновесия плоской системы сил
- •1.4.2. Пример решения задачи на равновесие твердого тела под действием плоской системы сил
- •1.4.3. Равновесие системы тел
- •1.4.4. Пример решения задачи на равновесие твердого тела под действием произвольной системы сил
- •Раздел 2. Кинематика
- •2.1. Кинематика точки
- •2.1.1. Кинематические способы задания движения точки
- •2.1.2. Скорость точки
- •2.1.3. Ускорение точки
- •2.1.4. Естественные оси
- •2.1.5. Проекции вектора ускорения точки на естественные оси
- •2.1.6. Пример решения задачи на кинематику точки
- •2.2. Простейшие движения твердого тела
- •2.2.1. Поступательное движение твердого тела
- •2.2.2. Вращение твердого тела вокруг неподвижной оси и кинематические характеристики этого движения
- •2.2.3. Скорости и ускорения точек твердого тела, вращающегося вокруг неподвижной оси
- •2.2.4. Векторные формулы для кинематических характеристик вращающегося твердого тела
- •2.2.5. Пример решения задачи на вращение твердого тела вокруг неподвижной оси
- •Раздел 3. Динамика
- •3.1. Динамика материальной точки
- •3.1.1. Основное уравнение динамики материальной точки в декартовых и естественных координатах
- •3.1.2. Две основные задачи динамики материальной точки
- •3.1.3. Инерциальные системы отсчета
- •3.2. Прямолинейные колебания материальной точки
- •3.2.1. Свободные гармонические колебания материальной точки
- •3.2.2. Пример решения задачи на свободные колебания точки
- •3.2.2. Свободные затухающие колебания материальной точки
- •3.2.3. Вынужденные колебания материальной точки
- •3.3. Теоремы об изменении количества движения и о движении центра масс механической системы
- •3.3.1. Механическая система
- •3.3.2. Количество движения материальной точки и системы
- •3.3.3. Теорема об изменении количества движения системы
- •3.3.4. Теорема о движении центра масс системы
- •3.3.5. Пример решения задачи на теорему о движении центра масс
- •3.4. Теорема об изменении кинетического момента механической системы относительно неподвижных центра и оси
- •3.4.1. Момент количества движения материальной точки относительно центра и оси
- •3.4.2. Кинетический момент системы относительно центра и оси
- •3.4.3. Кинетический момент твердого тела, вращающегося вокруг неподвижной оси
- •3.4.4. Осевые моменты инерции однородных тел простейшей геометрической формы
- •3.4.5. Теоремы об изменении кинетического момента системы относительно неподвижных центра и оси
- •3.4.6. Дифференциальное уравнение вращения твердого тела вокруг неподвижной оси
- •3.4.7. Пример решения задач на теорему об изменении кинетического момента системы
- •3.5. Теорема об изменении кинетической энергии механической системы
- •3.5.1. Кинетическая энергия материальной точки, твердого тела и механической системы
- •3.5.2. Кинетическая энергия твердого тела
- •3.5.3. Работа и мощность силы
- •3.5.4. Работа силы тяжести и силы упругости
- •3.5.5. Работа и мощность сил, приложенных к твердому телу, вращающемуся вокруг неподвижной оси
- •3.5.6. Теорема об изменении кинетической энергии материальной точки
- •3.5.7. Теорема об изменении кинетической энергии системы
- •3.5.8. Потенциальное силовое поле
- •3.5.9. Закон сохранения механической энергии
- •3.5.10. Пример решения задачи на теорему об изменении кинетической энергии механической системы
- •Заключение
- •3.3. Глоссарий (краткий словарь терминов)
- •4. Блок контроля освоения дисциплины
- •4.1. Задания на контрольные работы и методические указания к их выполнению
- •4.1.1. Общие указания
- •4.1.2. Указания к выполнению контрольной работы 1 (Таблица 1)
- •4.1.3. Указания к выполнению контрольной работы 2 (Таблица 2)
- •4.1.4. Указания к выполнению контрольной работы 3 (Таблица 3)
- •4.1.5. Указания к выполнению контрольной работы 4 (Таблица 4)
- •4.1.6. Указания к выполнению контрольной работы 3 (Таблица 5)
- •4.1.7. Указания к выполнению контрольной работы 4 (Таблица 6)
- •4.2. Тестовые задания текущего контроля
- •4.3. Итоговый контроль. Вопросы к экзамену
3.4.5. Теоремы об изменении кинетического момента системы относительно неподвижных центра и оси
Рассмотрим механическую систему, состоящую из материальных точек и движущуюся относительно инерциальной системы отсчета под действием системы внешних и внутренних сил. Движение системы описывается системой дифференциальных уравнений (51).
Сложим
почленно левые и правые части этих
уравнений, предварительно умножив
каждое из них векторно слева на
соответствующий радиус-вектор
,
где
![]() .
.
Тогда получим
![]() .
(79)
.
(79)
Вычислим производную по времени от количества движения -ой точки:
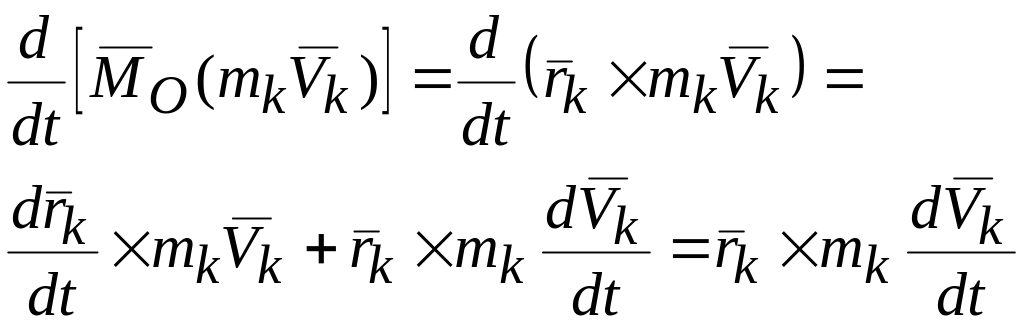 .
.
Здесь
учтено, что
![]() и
и
![]() ,
поскольку векторное произведение
коллинеарных векторов
и
равно нулю.
,
поскольку векторное произведение
коллинеарных векторов
и
равно нулю.
Если
обозначить
![]() ;
;
![]() ,
то сумма уравнений (79) может быть записана
в виде:
,
то сумма уравнений (79) может быть записана
в виде:
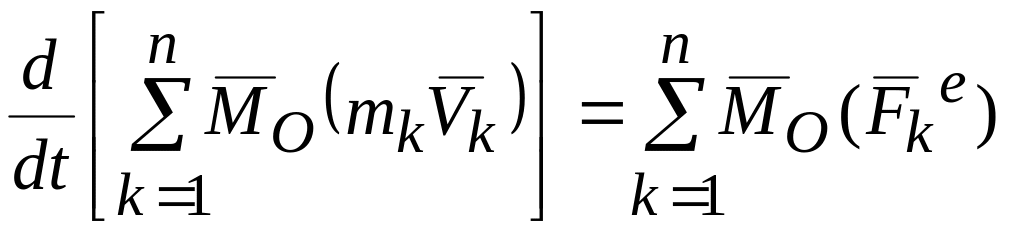 ,
или
,
или
![]() .
(80)
.
(80)
Здесь
учтена формула (70), а также следующее
обстоятельство: складывая попарно
моменты всех внутренних сил системы и
учитывая, что в соответствии с третьим
законом механики они попарно равны по
модулю и противоположны по направлению,
имеем
![]() ,
то есть геометрическая сумма всех
внутренних сил (главный момент) для
системы равна нулю.
,
то есть геометрическая сумма всех
внутренних сил (главный момент) для
системы равна нулю.
Уравнение (80) выражает теорему об изменении кинетического момента механической системы: производная по времени от кинетического момента системы относительно неподвижного центра равна геометрической сумме моментов (главному моменту) всех внешних сил относительно того же центра.
Проектируя обе части уравнения (80) на неподвижные оси , получим с учетом (72) три алгебраические уравнения:
![]() ,
,
![]() ,
,
![]() ,
(81)
,
(81)
где
![]() - кинетические моменты системы относительно
осей
- кинетические моменты системы относительно
осей
![]() ,
а
,
а
![]() ,
,
![]() ,
,
![]() - главные моменты внешних сил относительно
тех же осей.
- главные моменты внешних сил относительно
тех же осей.
Из доказанной теоремы вытекают следующие следствия:
1) Внутренние силы непосредственно не влияют на изменение кинетического момента системы. Это вытекает из того, что главный момент всех внутренних сил для системы равен нулю (см. вывод уравнения (80)).
2)
Если
![]() ,
то
,
то
![]() и
и
![]() .
.
Если главный момент внешних сил относительно неподвижного центра равен нулю, то кинетический момент системы относительно того же центра сохраняется постоянным.
3)
Если
![]() ,
то
,
то
![]() и
и
![]() .
.
Если главный момент внешних сил относительно неподвижной оси равен нулю, то кинетический момент системы относительно той же оси сохраняется постоянным.
Последние два следствия называются законами сохранения кинетического момента системы.
Практическим преимуществом доказанной теоремы является то, что моменты внутренних сил непосредственно не влияют на изменение кинетического момента системы.
3.4.6. Дифференциальное уравнение вращения твердого тела вокруг неподвижной оси
Р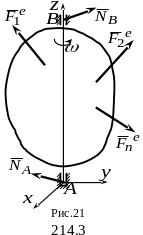 ассмотрим
некоторое твердое тело, вращающееся
вокруг неподвижной оси
,
и на которое действуют система внешних
сил
ассмотрим
некоторое твердое тело, вращающееся
вокруг неподвижной оси
,
и на которое действуют система внешних
сил
![]() и реакции опор
и
и реакции опор
и
![]() (рис. 20).
(рис. 20).
Для решения задачи о вращении этого тела используем теорему об изменении кинетического момента системы относительно оси (третье уравнение системы (81)):
. (82)
Кинетический момент этого тела согласно (76) равен .
Поскольку момент инерции является постоянной величиной, то уравнение (82) можно записать в форме:
![]() .
(83)
.
(83)
Это уравнение называется дифференциальным уравнением вращения твердого тела вокруг неподвижной оси.
Используя
формулы кинематики
![]() ,
перепишем уравнение (83) в виде:
,
перепишем уравнение (83) в виде:
![]() .
(84)
.
(84)
Сравним
уравнение (84) с дифференциальным
уравнением поступательного движения
твердого тела, например, в направлении
оси
(первое уравнение системы (66)). Если при
поступательном движении силовым фактором
является проекция
![]() главного вектора внешних сил на ось
,
то при вращении – главный момент
внешних сил относительно оси
;
аналог же линейного ускорения
главного вектора внешних сил на ось
,
то при вращении – главный момент
внешних сил относительно оси
;
аналог же линейного ускорения
![]() центра масс тела – угловое ускорение
центра масс тела – угловое ускорение
![]() .
Аналогом массы тела, как меры инертности
тела при его поступательном движении,
является момент инерции
,
как мера инертности тела при его вращении
вокруг неподвижной оси. С помощью
дифференциальных уравнений (83) и (84)
можно решать как прямую, так и обратную
задачи динамики вращения твердого тела
вокруг неподвижной оси.
.
Аналогом массы тела, как меры инертности
тела при его поступательном движении,
является момент инерции
,
как мера инертности тела при его вращении
вокруг неподвижной оси. С помощью
дифференциальных уравнений (83) и (84)
можно решать как прямую, так и обратную
задачи динамики вращения твердого тела
вокруг неподвижной оси.
