3.1.2. Две основные задачи динамики материальной точки

Имея уравнения динамики материальной точки, можно сформулировать две основные задачи динамики: прямую и обратную.

Прямой называется задача, в которой по заданным движению и массе точки следует определить силы, действующие на эту точку.

Обратной называется задаче, в которой по заданным силам, действующим на точку массы , следует найти движение точки.

Рассмотрим прямую задачу динамики точки. Если кинематические уравнения движения заданы, например, в декартовой системе координат:

,

а масса точки известна, то согласно системе уравнений (3) равнодействующая сил, действующих на точку, будет иметь проекции:

, , . (5)

Тогда модуль равнодействующей будет равен:

; (6)

а направляющие косинусы:

, , . (7)

Таким образом, равнодействующая определяется путем дифференцирования по времени заданных кинематических уравнений движения.

Проиллюстрируем прямую задачу динамики примером.

Пример. 1 Материальная точка движется в горизонтальной плоскости согласно уравнениям , где - положительные постоянные. Определить силу, вызывающую это движение.

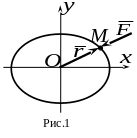Решение. Дважды дифференцируя по времени заданные уравнения движения, найдем проекции ускорения на оси декартовой системы координат:

Проекции искомой силы согласно (5) будут равны:

Отсюда:

.

Таким образом, модуль искомой силы пропорционален модулю радиус-вектора движущейся точки (рис. 1).

С другой стороны, имеем:

,

,

Сравнивая выражения для направляющих косинусов векторов и , заключаем, что эти вектора направлены по одной прямой в противоположные стороны, то есть сила является силой притяжения к центру (рис. 1).

Рассмотрим теперь обратную задачу динамики. Пусть заданы силы, действующие на свободную точку массы ; требуется определить закон движения точки.

Силы, действующие на точку, могут являться функциями положения точки, характеризуемого радиус-вектором , ее скорости , а также времени . Поэтому в общем случае закон изменения силы имеет вид:

Определение движения материальной точки по заданным силам сводится к нахождению закона ее движения

,

то есть к интегрированию дифференциальных уравнений вида:

,

, (8)

;

к которым в этом случае сводятся уравнения динамики (3).

Уравнения (8) образуют систему трех совместных дифференциальных уравнений второго порядка. Предположим, что нам удалось проинтегрировать систему (8) и получить общее решение вида:

, (9)

где - произвольные постоянные интегрирования.

Если постоянным интегрирования в соотношениях (9) давать различные числовые значения, то можно получить множество различных решений вида (9). Значит под действием одних и тех же сил можно получить множество различных решений, это физически означает, что точка может совершать различные движения.

Поэтому, кроме задания сил, действующих на материальную точку, необходимо задать еще и начальные условия ее движения:

при . (10)

Подставляя начальные условия (10) в уравнения (9), получим систему шести уравнений для определения постоянных интегрирования:

;

.

Решая эти уравнения относительно постоянных , найдем эти постоянные:

, . (11)

Подставляя найденные значения постоянных в общее решение(9), получим частное решение системы уравнений (8), удовлетворяющее начальным условиям (10), то есть уравнения движения точки, соответствующие начальным условиям конкретной задачи:

(12)

.

Проиллюстрируем обратную задачу динамики примером.

Пример 2 Самолет весом летит по горизонтальной прямолинейной траектории. Сила тяги постоянна и составляет угол с направлением полета. Сопротивление воздуха пропорционально квадрату скорости: , где - постоянный положительный коэффициент. Определить, какое расстояние пролетит самолет, прежде чем его скорость увеличится с некоторого значения до значения . Определить также условие, при котором полет самолета будет действительно горизонтальным.

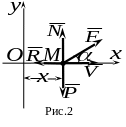Решение. Будем рассматривать поступательное движение самолета как движение материальной точки , к которой приложены сила тяжести , сила тяги , составляющая угол с направлением вектора скорости , подъемная аэродинамическая сила и сила сопротивления воздуха (рис. 2).

Совместим ось системы отсчета с горизонтальной траекторией самолета и составим дифференциальное уравнение движения точки в проекции на ось :

.

Сделаем замену , где - алгебраическая величина скорости. Далее выполним подстановку, введя аргумент вместо :

.

Тогда дифференциальное уравнение примет вид:

.

Получили дифференциальное уравнение первого порядка с разделяющимися переменными и . Разделяем переменные и интегрируем левую и правую части этого уравнения в соответствующих, заданных условиями задачи , пределах:

при ; при .

;

, .

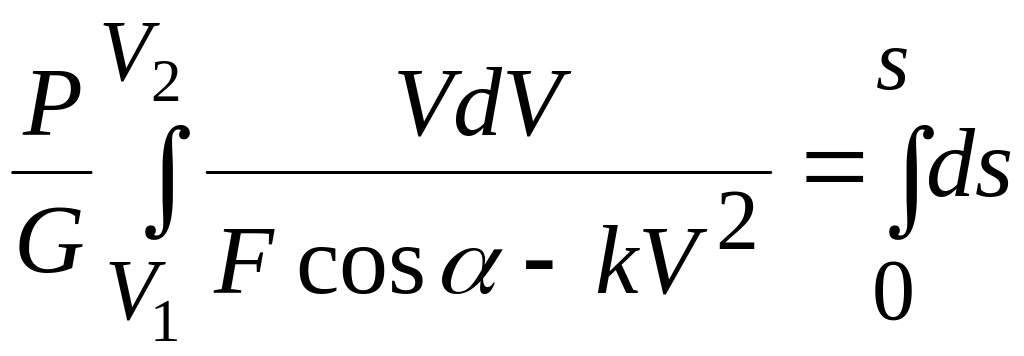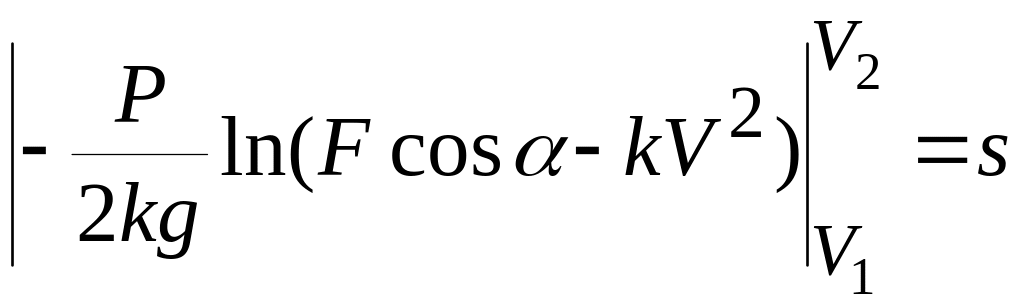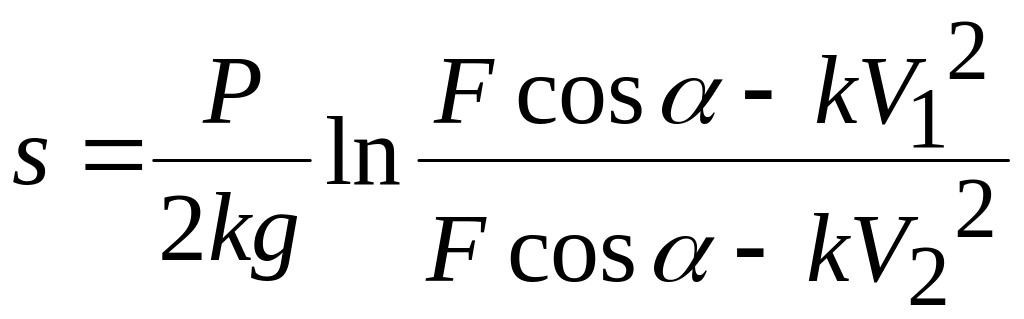Для определения условия горизонтальности полета составим дифференциальное уравнение движения самолета в проекции на ось :

.

Так как при горизонтальном полете , то , и уравнение примет вид уравнения равновесия:

,

что и является условием горизонтальности полета.