3.2.3. Вынужденные колебания материальной точки
Рассматриваемые
до сих пор свободные колебания материальной
точки происходили под действием
восстанавливающей силы
и силы сопротивления
.
Эти силы не только влияют на движение
точки , но и сами управляются этим
движением, поскольку они зависят от
координаты
и скорости
.
Р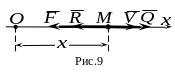
ассмотрим
случай, когда на точку, кроме этих сил,
действует еще и возмущающая сила,
описываемая как функция времени
и не зависящая от движения самой точки.
Подобные силы возникают при работе
различных машин и механизмов. Будем
рассматривать важный для технических
приложений случай, когда проекция этой
силы на ось
равна
,
(37)
где
- амплитуда, а
- частота возмущающей силы (рис. 9).
Дифференциальное уравнение движения т очки в проекции на ось имеет вид:
.
Приведем его к следующему виду, используя обозначения, рассмотренные при изучении свободных колебаний:
,
(38)
где
,
,
.
Общее
решение этого неоднородного линейного
дифференциального уравнения второго
порядка , как известно, складывается из
общего решения
соответствующего однородного уравнения
и частного решения
исходного уравнения (38).
Решение , описываемое уравнением (31), было найдено ранее для случая свободных затухающих колебаний; частное же решение будем искать в виде:
,
(39)
где - амплитуда и - сдвиг фаз вынужденных колебаний, подлежащие определению.
Подставляя
функцию (39) и ее производные
и
в уравнение (38), получим:
.
(40)
Отметим, что в правой части этого уравнения выполнены следующие тождественные преобразования:
.
Функция
(39) будет частным решением уравнения
(38), если она обращает это уравнение в
тождество, которое будет справедливо
при любом значении
.
А для этого необходимо, чтобы коэффициенты
при
и
в правой и левой частях равенства (40)
были бы равны.
Это позволяет получить систему двух алгебраических уравнений
.
(41)
Из
этих уравнений, используя равенство
,
легко находим амплитуду и сдвиг фаз
вынужденных колебаний:
;
(42)
.
(43)
Итак, общее решение уравнения (38) имеет вид:
,
(44)
где произвольные постоянные и находятся из начальных условий движения.
Из уравнения (44) видно, что колебания складываются из свободных затухающих колебаний с частотой и гармонических вынужденных колебаний с частотой возмущающей силы . Поскольку с ростом времени слагаемое стремится к нулю, то с течением времени устанавливаются вынужденные колебания с частотой возмущающей силы; причем их амплитуда и сдвиг фазы определяются зависимостями (42) и (43) и не зависят от начальных условий.
Запишем формулу (42) для амплитуды вынужденных колебаний в следующем виде:
;
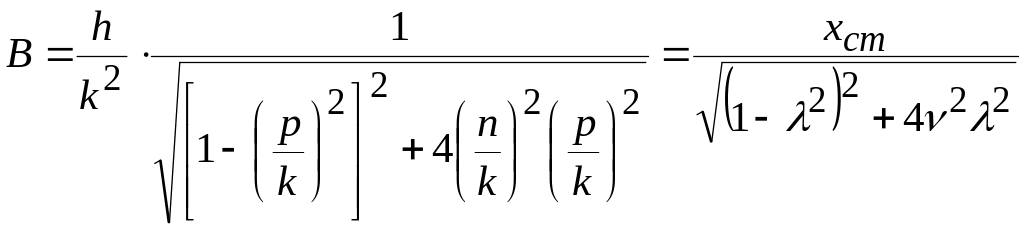(45)
где
- коэффициент
расстройки;
;
-
статическое
отклонение
точки при действии на нее постоянной
силы
.
Коэффициент динамичности
(46)
показывает,
как изменяется амплитуда вынужденных
колебаний, отнесенная к статическому
отклонению, при действии силы
в зависимости от частоты
и коэффициента
.
График функции
называется резонансной
кривой.
На
рис. 10 представлены резонансные кривые
для различных значений
.
Семейство кривых расположено ниже
кривой, отвечающей отсутствию сопротивления
.
В случае, когда
амплитуда (и коэффициент динамичности)
с увеличением
монотонно уменьшается.
Когда
частота возмущающей силы мала по
сравнению с собственной частотой
,
коэффициент динамичности близок к
единице. В другом крайнем случае, когда
частота
велика по сравнению с собственной
частотой
,
коэффициент
весьма мал; соответственно мала и
амплитуда
.
В отмеченных крайних случаях резонансные кривые сходятся очень близко, то есть сила сопротивления в этих случаях практически не влияет на величину и .
К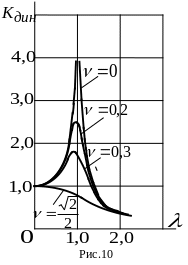
огда
же частоты
и
сближаются, коэффициент динамичности
и амплитуда
быстро возрастают и их значения уже
существенно зависят от степени
сопротивления. Максимум
достигается, вообще говоря, при значении
,
несколько меньшим единицы.
Приравнивая
нулю производную
можно найти, что
достигает максимума при значении
или при значении , равным:
.
(47)
Максимальное значение амплитуды вынужденных колебаний будет при этом равно
.
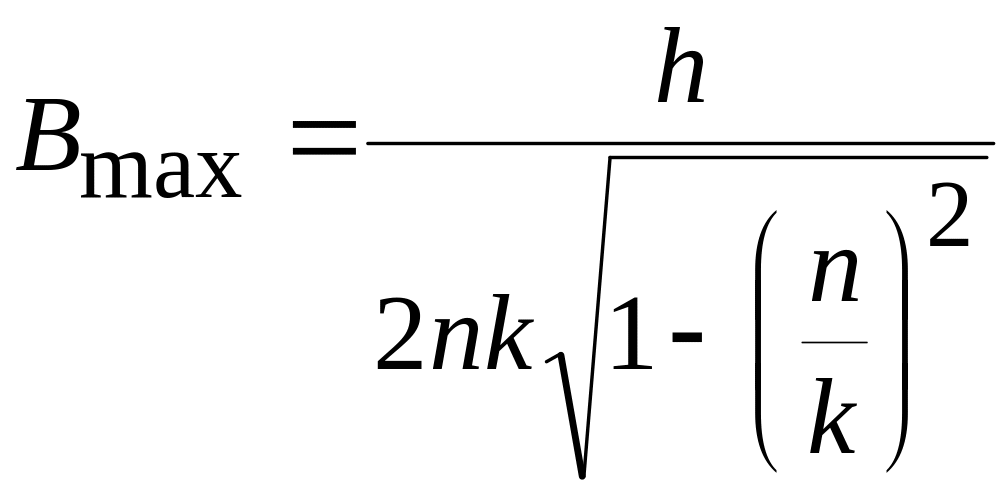(48)
Однако,
поскольку коэффициент
весьма мал по сравнению с
,
то с достаточной степенью точности
можно считать, что амплитуда приобретает
максимальное значение при
.
В этом случае
,
(49)
то есть наибольшее значение амплитуды вынужденных колебаний обратно пропорционально коэффициенту сопротивления .
Явление, при котором частота вынуждающей силы близка к собственной частоте, а амплитуда вынужденных колебаний достигает максимального значения, называется резонансом.
С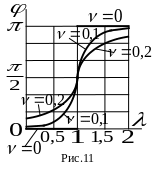
двиг
фаз между вынужденными колебаниями и
возмущающей силой, определяемый формулой
(43), можно представить в виде:
.
(50)
График
зависимости
представлен на рис. 11. На нем изображены
кривые функции
для различных значений
.
При
;
при
;
при
.
При
и при отсутствии сопротивления
имеет место скачкообразное изменение
сдвига фаз
от
до
.
Вынужденные колебания очки при отсутствии действия силы сопротивления изучаются самостоятельно (см. [1], с. 48-53 или [2], с. 285-287).
Вопросы для самопроверки по теме 3.2
1. Дайте определение восстанавливающей силы. Приведите примеры восстанавливающих сил.
2. Составьте дифференциальное уравнение свободных гармонических колебаний материальной точки.
3. Что такое период и частота свободных колебаний?
4. Дайте определение амплитуды свободных гармонических колебаний, фазы этих колебаний.
5. Напишите общее решение дифференциального уравнения свободных колебаний без учета действия силы сопротивления, с учетом ее действия.
6. Какие характеристики свободных колебаний не зависят от начальных условий?
7. Дайте определение декремента колебаний.
8. Что такое период свободных затухающих колебаний? Какова его связь с периодом свободных гармонических колебаний?
9. Напишите дифференциальное уравнение вынужденных колебаний материальной точки.
10. Чему равна частота вынужденных колебаний?
11. Напишите формулы для амплитуды вынужденных колебаний.
12. Какие факторы влияют на величину амплитуды вынужденных колебаний?
13. Дайте определение явления резонанса.
14. Напишите формулы для амплитуды вынужденных колебаний при резонансе.
15. Чему равен сдвиг фаз резонансных колебаний?
16. Что называется коэффициентом динамичности?
17. Решите самостоятельно задачи 32.2, 32.3, 32.16, 32.35, 32.51, 32.72, 32.82, из [3].