3.4.7. Пример решения задач на теорему об изменении кинетического момента системы

Пример 5 На вал, вращающийся с угловой скоростью , насажен маховик весом 1000 и диаметром (рис. 22). В некоторый момент времени к маховику был приложен постоянный тормозной момент , в результате чего через минуты вал остановился. Считая маховик однородным диском, а также пренебрегая трением в опорах и весом самого вала, определить модуль тормозного момента.

Р ешение. В состав механической системы входит твердое тело – вал с маховиком, вращающимся вокруг неподвижной оси . На вал действуют внешний тормозной момент , а также внешние силы: - вес вала с маховиком, , - реакции опор и .

Запишем дифференциальное уравнение вращения твердого тела вокруг неподвижной оси (83), которое в условиях данной задачи имеет вид:

,

или , (а)

где - момент инерции маховика относительно оси ;

, поскольку моментами трения в опорах пренебрегаем по условию, а моменты внешних сил , , равны нулю, так как их линии действия пересекают ось ,

Разделим переменные в уравнении (а)

и в результате интегрирования находим

.

Постоянную интегрирования находим из начального условия -

при : .

Таким образом, частное решение уравнения (а) будет иметь вид

. (б)

Это уравнение выражает зависимость угловой скорости вала от времени. В момент остановки вала имеем , .

В результате из уравнения (б) определяем момент :

Вопросы для самопроверки по теме 3.4.

1) Дайте определение момента количества движения точки относительно неподвижных центра и оси.

2) В чем заключается отличие момента силы от момента количества движения?

3) В каких случаях момент количества движения точки относительно центра, а также относительно оси, равен нулю?

4) Что такое кинетический момент системы относительно неподвижных центра и оси?

5) Сформулируйте теорему об изменении кинетического момента системы относительно центра и оси.

6) В каком случае кинетический момент системы сохраняется постоянным? – равным нулю?

7) Определите кинетический момент твердого тела, вращающегося вокруг неподвижной оси

8) Могут ли внутренние силы изменить кинетический момент системы и почему?

9) Могут ли внутренние силы и их моменты косвенно повлиять на изменение движения системы?

10) Дайте определение момента инерции твердого тела относительно оси; радиуса инерции тела относительно оси.

11) Напишите дифференциальное уравнение вращения твердого тела вокруг неподвижной оси.

12) При каких условиях тело вращается вокруг неподвижной оси равномерно? – равноускоренно? – замедленно?

13) Каков физический смысл момента инерции твердого тела относительно оси?

14) Решите самостоятельно задачи 37.5,.37.9, 37.15, 37.52 из [3].

3.5. Теорема об изменении кинетической энергии механической системы

3.5.1. Кинетическая энергия материальной точки, твердого тела и механической системы

Кинетической энергией материальной точки называется скалярная положительная мера ее движения, определяемая формулой

,

где - масса точки; - модуль ее скорости.

Кинетической энергией механической системы называется арифметическая сумма кинетических энергий всех ее точек

. (85)

Если в качестве системы рассматривается механизм или машина, то кинетическая энергия определяется следующей формулой

, (86)

где - кинетическая энергия подвижного звена механизма с номером , - число подвижных звеньев, которые рассматриваются как твердые тела.

Рассмотренные формулы для кинетической энергии содержат абсолютные скорости, измеряемые относительно инерциальной (абсолютной) системы отсчета. Однако во многих случаях движение системы полезно представить как сложное, состоящее из поступательного движения вместе с центром масс и относительного движения по отношению к центру масс.

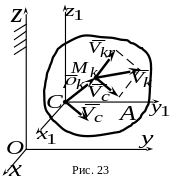Введем в рассмотрение, кроме инерциальной системы отсчета , систему отсчета , поступательно движущуюся относительно инерциальной (рис. 23). Абсолютная скорость произвольной точки некоторой механической системы определится как геометрическая сумма скорости центра масс и относительной скорости этой точки по отношению к центру масс (смотри тему 2.3):

.

Из векторной алгебры известно, что

, .

Тогда кинетическая энергия системы будет равна

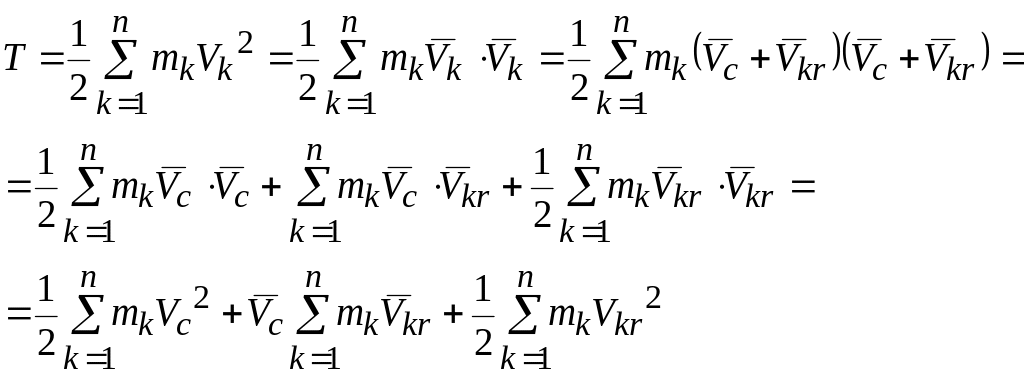
В этой формуле первое слагаемое можно представить в виде

,

где - масса всей системы.

Проведем из центра масс системы радиус-векторы во все точки системы. Радиус-вектор центра масс с учетом формулы (61) темы3.3 будет равен:

.

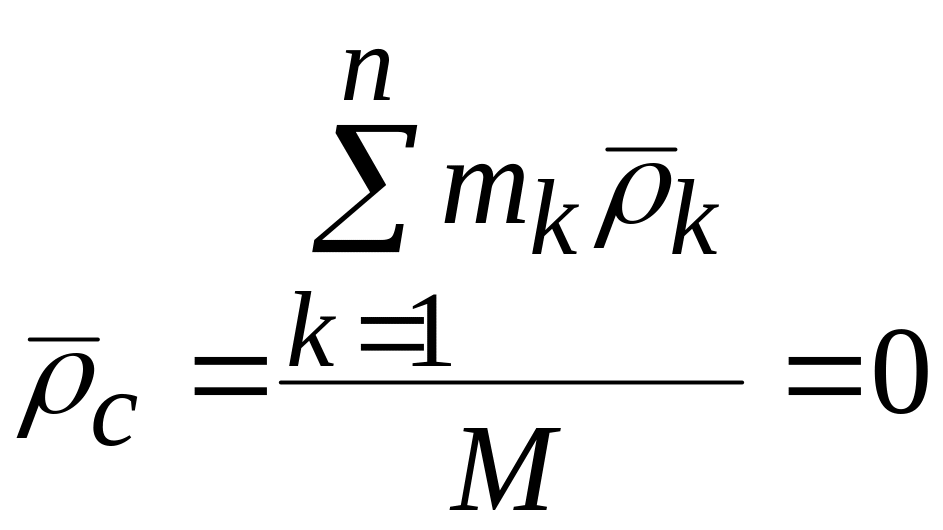Поэтому и, следовательно,

Действительно, радиус-вектор проведен из начала подвижной системы отсчета , а производная представляет собой относительную скорость точки .

Итак, второе слагаемое обращается в ноль.

Третье слагаемое представляет собой кинетическую энергию системы в ее относительном движении по отношению к центру масс.

Окончательно получим:

. (87)

Это соотношение выражает теорему Кенига, которая формулируется следующим образом: кинетическая энергия механической системы в абсолютном движении равна сумме кинетической энергии центра масс системы, в котором мысленно сосредоточена ее масса, и кинетической энергии системы в ее относительном движении по отношению к центру масс.