3.3. Теоремы об изменении количества движения и о движении центра масс механической системы

3.3.1. Механическая система

В предыдущих темах изучалась динамика одной материальной точки. Практически же в технике чаще встречаются задачи, когда движение одной материальной точки нельзя изучать изолированно от движения других точек или тел. Это приводит к необходимости перейти от динамики точки к изучению динамики механической системы. Механической системой называется совокупность материальных точек или тел, движения которых взаимосвязаны. Механической системой будут являться Солнечная планетная система, какой-либо механизм или машина.

Силы, приложенные к точкам системы можно разделить на внешние и внутренние. Внешними называются силы, действующие на систему извне. Внутренними называются силы взаимодействия между материальными точками самой системы. Отметим, что в состав внешних и внутренних сил могут входить как активные силы, так и реакции связей. В дальнейшем условимся обозначать внешнюю силу , а внутреннюю - .

Рассмотрим механическую систему, состоящую из материальных точек. Применяя принцип освобождаемости от связей (см. тему 1.1), заменим связи их реакциями. Обозначим через и равнодействующие соответственно внешних и внутренних сил, приложенных к точке системы с номером . С учетом уравнения (1) опишем движение этой системы следующими уравнениями:

, (51)

где и - масса и ускорение -ой точки системы.

В проекциях на оси инерциальной декартовой системы координат имеем:

; ; , (52)

.

Уравнения (52) представляют собой систему дифференциальных уравнений движения материальных точек всей системы.

Решение задачи динамики механической системы путем интегрирования системы дифференциальных уравнений (52) практически нереализуемо, поскольку внутренние силы и входящие в число внешних сил реакции связей заранее неизвестны, а число точек системы может быть достаточно велико.

В связи с этим в теоретической механике разработаны методы, позволяющие в какой-то степени обойти указанные трудности. При этом в рассмотрение вводятся векторные и скалярные величины, характеризующие движение механической системы в целом и называемые мерами движения системы. К числу таких мер относятся количество движения, момент количества движения (кинетический момент) и кинетическая энергия механической системы.

3.3.2. Количество движения материальной точки и системы

Количеством движения материальной точки называется вектор , равный произведению массы точки на вектор ее скорости, а направление которого совпадает с направлением вектора скорости.

Количеством движения механической системы называется геометрическая сумма количеств движения всех ее точек:

, (53)

где - количество движения -ой точки.

Отметим, что вектор является свободным вектором.

3.3.3. Теорема об изменении количества движения системы

Пусть имеется механическая система, состоящая из материальных точек и движущаяся под действием внешних и внутренних сил относительно инерциальной системы отсчета . Движение этой системы описывается системой уравнений (51).

Сложив почленно левые и правые части этих уравнений, получим:

. (54)

Представим левую часть полученного уравнения в виде

. (55)

Складывая попарно внутренние силы и учитывая, что по третьему закону механики они равны по модулю и противоположны по направлению, имеем , то есть геометрическая сумма (главный вектор) всех внутренних сил системы равна нулю. Окончательно из уравнений (54) и (55) получим:

. (56)

Уравнение (56) выражает теорему об изменении количества движения системы в дифференциальной форме: производная по времени от количества движения механической системы равна геометрической сумме (главному вектору) всех внешних сил, приложенных к системе.

Проектируя обе части уравнения (56) на оси координат , получим

, (57)

где ; ; - проекции вектора на эти оси.

Умножим уравнение (56) на и проинтегрируем обе его части в соответствующих пределах:

; ;

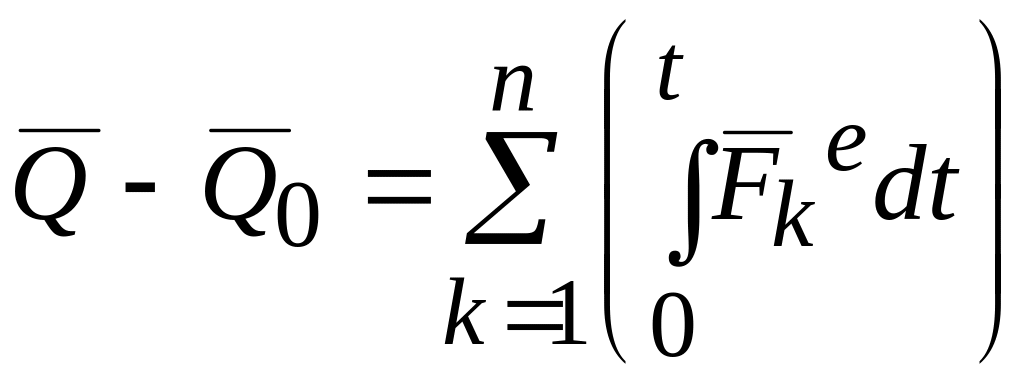или

. (58)

Здесь и - значения количества движения системы в моменты времени и ; а

(59) –

импульс внешней силы за промежуток времени .

Уравнение (58) выражает теорему об изменении количества движения системы в конечной форме: изменение количества движения механической системы за некоторый промежуток времени равно сумме импульсов всех внешних сил, приложенных к системе за тот же промежуток времени.

Векторному уравнению (58) соответствуют три алгебраических уравнения:

; ; ; (60)

где ; ; - проекции импульса на оси координат.

Из доказанной теоремы вытекают следующие следствия:

1) Внутренние силы непосредственно не влияют на изменение количества движения системы.

Однако, следует отметить, что в некоторых случаях за счет действия внутренних сил могут появиться внешние силы, влияющие на изменение количества движения системы.

2) Если , то тогда согласно (56) и .

Если сумма всех внешних сил, приложенных к системе , равна нулю, то количество движения системы сохраняется постоянным.

3) Если , то тогда согласно первому из уравнений (57) имеем и .

Если сумма проекций всех внешних сил, приложенных к системе, на какую-либо ось равна нулю, то проекция количества движения системы на ту же ось сохраняется постоянной.

Последние два следствия называются законами сохранения количества движения системы.