3.3.5. Пример решения задачи на теорему о движении центра масс

Пример 1. К оси ведомого колеса радиуса приложена движущая сила , направленная горизонтально и равная по модулю , где - масса колеса, - коэффициент трения скольжения, - ускорение свободного падения. Определить уравнение движения центра масс колеса, если его движение начинается из состояния покоя.

Решение. Отнесем движение данной механической системы, представленной твердым телом (колесом), совершающим плоское движение, к инерциальной условно неподвижной системе отсчета (рис. 12).

На колесо действуют следующие внешние силы: активные силы и , а также реакции связи (реакция плоскости) и (сила трения скольжения).

П рименяя теорему о движении центра масс системы, составим дифференциальные уравнения движения точки тела в проекции на оси и :

; . (а)

Центр масс колеса движется вдоль пунктирной линии, параллельной оси (рис. 12).

Поскольку колесо катится по плоскости дороги , не отрываясь от нее, то и . Второе уравнение (а) обращается в уравнение равновесия:

; ;

По закону Кулона наибольшее значение силы трения, имеющее место при наличии проскальзывания, равно

.

Тогда первое дифференциальное уравнение (а) примет вид:

,

или . (б)

Интегрируя это уравнение, получим общее решение

; . (в)

Запишем начальные условия: при , , ,

тогда будем иметь, что .

Окончательно, частное решение уравнения (б) будет иметь вид:

,

это и есть закон движения центра масс колеса.

Вопросы для самопроверки по теме 3.3

1. Дайте определение механической системы. Приведите примеры механических систем

2. На какие две группы можно разделить силы, действующие на точки системы?

3. Чему равен главный вектор внутренних сил механической системы?

4. Что называется количеством движения точки (системы)?

5. Дайте определение конечного импульса силы.

6. Чему равна сумма импульсов внутренних сил, действующих на систему? Почему?

7. Сформулируйте теорему об изменении количества движения механической системы в дифференциальной и интегральной формах

8. Дайте определение центра масс системы. В каких случаях можно заменить понятие центра масс понятием центра тяжести?

9. Выразите количество движения системы через ее массу; используйте понятие центра масс.

10. В каких задачах динамики твердое тело можно считать материальной точки?

11. Сформулируйте теорему о движении центра масс системы.

12. В чем заключается закон сохранения количества движения системы?

13. Твердое тело вращается вокруг неподвижной оси, проходящей через центр масс. Определите количество движения тела.

14. Самостоятельно решите задачи 35.4, 35.10, 35.17, 35.20 из [3].

3.4. Теорема об изменении кинетического момента механической системы относительно неподвижных центра и оси

3.4.1. Момент количества движения материальной точки относительно центра и оси

Понятие момента количества движения точки математически аналогично понятию момента силы (смотри тему 1.2).

Пусть точка движется относительно неподвижной системы координат ; положение точки определяется ее радиус-вектором , а ее количество движения равно (рис. 13). Напомним, что моментом силы относительно центра является вектор , приложенный в этом центре.

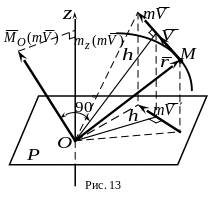Аналогично вводится понятие момента количества движения точки относительно центра :

. (67)

Вектор приложен в центре и в соответствии с правилом векторного произведения направлен перпендикулярно плоскости , проходящей через вектор и центр , в ту сторону, откуда движение точки видно происходящим в направлении против хода часовой стрелки. Модуль этого вектора равен

, (68)

где - плечо вектора относительно центра .

Аналогично понятию момента силы относительно оси, вводится понятие момента количества движения точки относительно оси.

Моментом количества движения точки относительно оси называется алгебраическая величина, равная произведению модуля проекции количества движения точки на плоскость (плоскость ), перпендикулярную к оси , на кратчайшее расстояние от точки до линии проекции (рис. 13):

. (69)