3.4.2. Кинетический момент системы относительно центра и оси

Кинетическим моментом системы относительно центра называется геометрическая сумма моментов количеств движения всех точек системы относительно того же центра:

. (70)

Кинетическим моментом системы относительно оси (например, оси ) называется алгебраическая сумма моментов количеств движения всех точек системы относительно оси :

. (71)

Между величинами и существует зависимость, аналогичная зависимости (19) в теме 1.2:

. (72)

3.4.3. Кинетический момент твердого тела, вращающегося вокруг неподвижной оси

Р ассмотрим твердое тело, вращающееся вокруг неподвижной оси с угловой скоростью (рис. 14). При этом некоторая точка тела движется по окружности с радиусом, равным расстоянию точки от оси . Скорость точки и ее количество движения направлены по касательной к этой окружности, то есть перпендикулярно радиусу в сторону вращения тела. Векторы и располагаются в плоскости, перпендикулярной оси вращения . Момент количества движения точки в соответствии с (69) равен:

. (73)

Здесь - проекция вектора скорости на касательную к траектории точки , равная в соответствии с формулой (88) из темы 2.2

.

Поэтому получим:

. (74)

Величина является алгебраической, ее знак определяется знаком , то есть направлением вращения тела вокруг оси .

В соответствии с (71) кинетический момент вращающегося твердого тела равен сумме моментов количеств движения всех точек твердого тела:

.

Здесь учтено, что является общим множителем при рассмотрении всех точек тела.

Введем обозначение

. (75)

Величина называется осевым моментом инерции тела относительно оси . Окончательно получим:

. (76)

Знак определяется знаком угловой скорости вращения твердого тела.

Определенный таким образом кинетический момент можно считать мерой вращения твердого тела вокруг неподвижной оси.

3.4.4. Осевые моменты инерции однородных тел простейшей геометрической формы

При изучении вращения твердого тела для полной характеристики распределения масс его точек кроме понятия центра масс необходимо ввести понятие центра инерции.

Из формулы (75) следует, что момент инерции является постоянной, положительной, скалярной величиной, не зависящей от движения тела и характеризующей распределение масс точек тела относительно оси вращения.

Моменты инерции однородных тел простой геометрической формы вычисляются путем интегрирования, их значения приводятся в технических справочниках и в учебных пособиях по механике.

Моменты инерции неоднородных тел сложной конфигурации вычисляются как путем их мысленного расчленения на фрагменты в виде простых геометрических форм, так и определяются экспериментально.

Иногда осевой момент инерции выражают через радиус инерции тела по формуле:

, (77)

где - масса тела.

Величины осевых моментов инерции некоторых однородных симметричных тел приводятся ниже.

А ) Однородный тонкий стержень

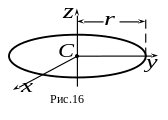
Б) Круглое тонкое кольцо (окружность)

В ) Круглый диск

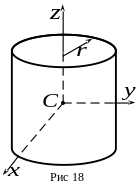
Г) Круглый цилиндр

Если известен момент инерции относительно центральной оси (оси, проходящей через центр масс тела), то можно определить момент инерции тела относительно любой оси, параллельной центральной. При этом и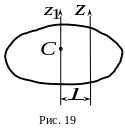 спользуется теорема Гюйгенса-Штейнера о моментах инерции относительно параллельных осей (рис.19): момент инерции тела относительно некоторой оси равен моменту инерции относительно оси , проходящей через центр масс тела параллельно оси , сложенному с произведением массы тела на квадрат расстояния между осями.

То есть . (78)