Лекция №10 Смешанные стратегии

Большинство матричных игр не имеет седловых точек. В такой ситуации игроку важно, чтобы противник не угадал, какую стратегию он будет использовать. Для осуществления этого плана следует пользовать­ся смешанной стратегией. Смешанная стратегия представляет собой схему случайного выбора чистой стратегии. Математически ее можно представить как вероятностное распределение на множестве чистых стра­тегий игрока.

Def. Пусть R – платежная матрица игры размера m×n.Тогда смешанная стратегия игрока А представляет собой вектор,удовлетворяющий условиям

,

а смешанная стратегия для игрока Б есть вектор,такой, что

.

Данное определение имеет следующий смысл: когда игрок Аис­пользует смешанную стратегиюp, он применяет случайный способ вы­бора стратегии, при котором чистая стратегиявыбирается с вероят­ностью, где. Аналогично игрокБ, используя смешанную стратегиюqприменяет случайный способ выбора стратегии, при кото­ром чистая стратегиявыбирается с вероятностью, гдеЭти две схемы рандомизации будем предполагать независимыми, так что вероятность того, что в партии игрокАвыберет стратегию, а игрокБ -, равна. Так как платеж в этом случае равен, математи­ческое ожидание результата игры (средний платеж игрокаА при розыг­рыше большого числа партий) выражается формулой

,

или в матричных обозначениях

,

где значок tозначает транспонирование.

Для смешанных стратегий седловая точка определяется как пара стратегий удовлетворяющих условию

для любых стратегий , гдеPиQ- множества допустимых смешанных стратегий игроковАиБ, соответственно.

Теорема. Каждая матричная игра имеет, по крайней мере, одну седловую точку в смешанных стратегиях.

Эта теорема носит название теоремы о минимаксе. Из нее следует, чтодля любой матричной игры

Величина Vобычно называетсяценойилизначением игры.

Def. Оптимальной называется такая стратегия игрока, которая гарантирует ему (в смысле математического ожидания) выигрыш, равный цене игры.

Таким образом, стратегия оптимальна для игрокаА,если

,

и стратегия оптимальна для игрока Б, если

.

Теорема о минимаксе гарантирует существование, по крайней ме­ре, одной оптимальной стратегии для каждого из игроков, т.е. матричные игры всегда имеют решение в смешанных стратегиях, и ниже мы рассмотрим алгоритмы его нахождения.

Методы определения оптимальных стратегий

1. Простейший метод состоит в нахождении седловой точки для чистых стратегий. Если такая седловая точка существует, то две чистые стратегии, которые к ней приводят, являются оптимальными.

2. Для уменьшения размерности игры используется доминирова­ние строк и столбцов.

Говорят, что k-я строка матрицыRдоминируетi-ю строку (т.е. од­на чистая стратегия доминирует другую), если

при всех j.

Аналогично l-й столбец доминируетj-й столбец, если

при всех i.

Заметим, что доминирующая стратегия никогда не хуже, а в неко­торых случаях и лучше, чем доминируемая. Игроку невыгодно использо­вать доминируемую стратегию, и она не должна войти в оптимальную смешанную страте­гию. Это позволяет при решении игры все доминируе­мые строки и столбцы отбросить, т.е. уменьшить размеры матрицы.

Пример

Рассмотрим игру с матрицей

.

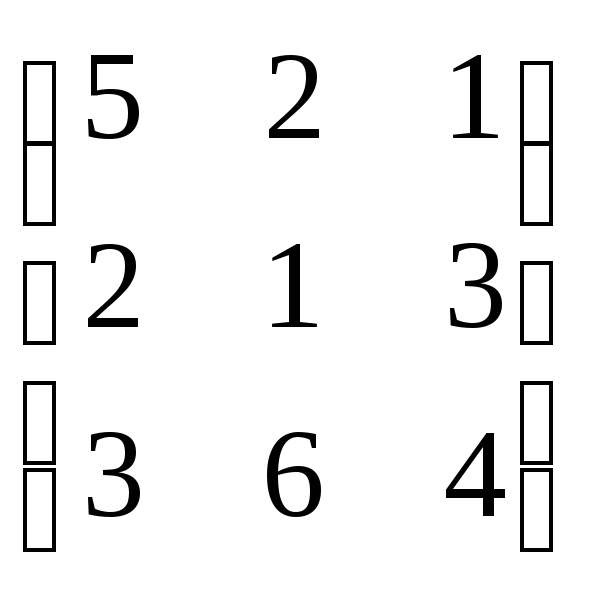Вторая строка доминирует третью. Исключение третьей строки приводит к матрице

.

Первый столбец в этой урезанной матрице доминирует второй. Исключе­ние второго столбца приводит к матрице

.

Найдя решение полученной игры, легко получить решение ис­ход­ной игры, приписав исключенным строкам и столбцам нулевые вероят­ности.

3. Существуют простые процедуры получения решения игр ма­лой размерности. Рассмотрим один из них на примере игры 22.

Пример

Рассмотрим игру с платежной матрицей

.

Эта игра не имеет решения в чистых стратегиях, так как

.

Будем искать решение этой игры в смешанных стратегиях.

Пусть pиq– вероятности выбора игрокамиАиБ, соответст­вен­но, первой чистой стратегии. Тогдаи(1-q)– вероятности выбора ими вто­рой чистой стратегии.

Математическое ожидание результата .

Для определения оптимальной стратегии игрока Анужно найти

.

Сначала при фиксированном значении pнеобходимо найти макси­мум поq, а для этого разобьем область измененияpна два интервала[0,0.4]и[0.4,1]знакопостоянства выражения(5p-2)и решим эту задачу на каждом из этих интервалов.

;

Итак, мы определили, что оптимальной для игрока Абудет сме­шан­ная стратегия, при которой первая чистая стратегия выбирается им с вероятностью (или частотой) 0,4, а вторая - с вероятностью 0,6. Цена игры - 3,2 .

Аналогично задача решается и для игрока Б.

С ростом размерности матрицы платежей сложность задачи замет­но воз­растает.

4. Для решения больших игр предложено несколько методов. Наи­бо­лее распространенным является определение опти­маль­ной стра­те­гии мето­да­ми линейного программирования.

Теорема.Каждой матричной игре mn с платежной матрицей R эквивалентна следующая пара двойственных задач линейного програм­мирования:

минимизировать целевую функцию при условиях

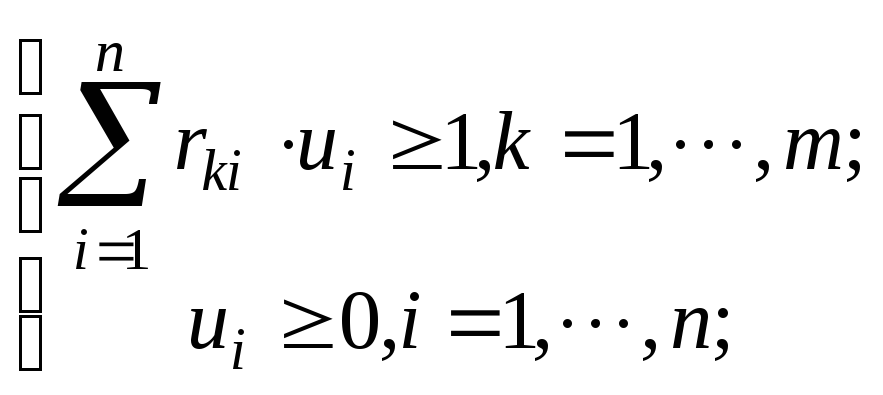(1)

максимизировать целевую функцию при условиях

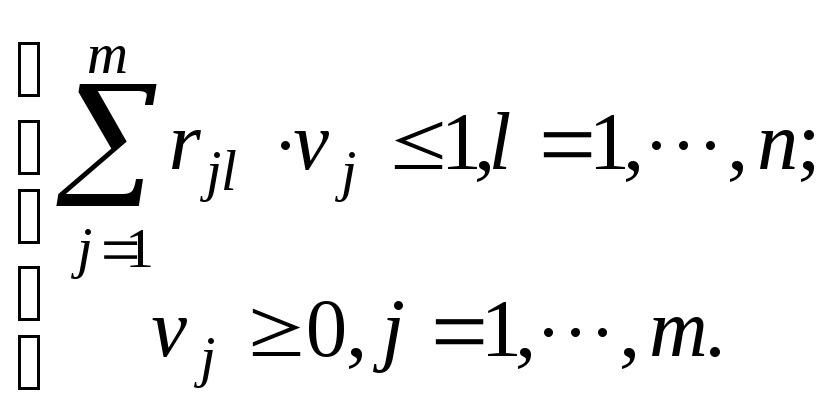(2)

Составляющие оптимальных смешанных стратегий игры и цена игры V связаны с компонентами оптимальных планов задачи ЛП со­от­но­шениями

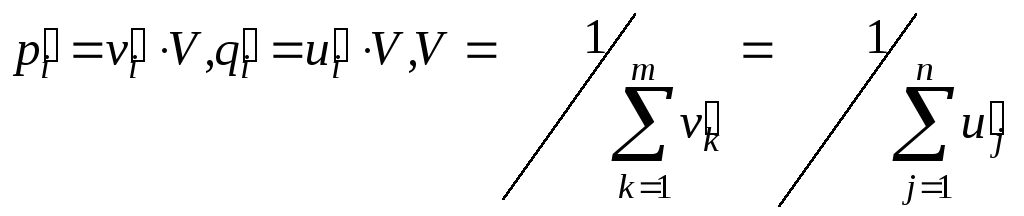(3)

Доказательство

Оптимальная стратегия должна обеспечить игрокуАпроиг­рыш, не боль­шийVпри любом поведении противника. В частности, если игрокБбу­дет использовать любую чистую стратегию, средний проигрыш не должен пре­выситьV, т.е. должны выполняться следующие неравенства

(4)

Допустим, что все элементы матрицы платежей R положительны. Этого всег­да можно добиться, прибавив ко всем элементам матрицы достаточно боль­шое положительное числоМ; при этом цена игры уве­ли­чит­ся наМ, а оп­тимальные стратегии не изменятся.

Тогда V>0и, разделив неравенства (4) наV, получим

(5)

где

Так как , то.

Гарантированный проигрыш игрока А-Vнужно миними­зи­ро­вать, т.е.- максимизировать.

Итак, мы доказали, что задача нахождения оптимальной страте­гии игрока Асводится к задаче линейного программирования (2) сmпере­меннымииnограничениями. Зная оптимальные значения, опти­мальную стратегиюpи цену игрыVможно найти по формулам (3) .

Аналогично доказывается, что задача нахождения оптимальной стратегии игрока Бсводится к задаче линейного программирования (2) .

Итак, вместо решения матричной игры можно решать эквива­лент­ную ей пару задач линейного программирования.

Справедливо и обратное утверждение: для любой задачи линейного программированияможет быть построена эквивалентная ей задача теории игр.