Лекция №13 Теория ожидаемой полезности

Простым распределением вероятностей p называется вещест­вен­ная функция, которая принимает положительные значения на боль­шинстве элементов x из конечного множества X, причем сумма всех значений p(x) равна 1.

Пусть P- множество всех простых распределений вероятностейp,q, ... , заданных на непустом множествеX. Следует отметить, что, если множествоXсодержит более одного элемента, то множествоPбудет не­ис­числимым.

Элементами Xмогут быть чистые стратегии или альтернативы, ли­бо же они могут представлять собой исходы (последствия) некоторых ре­шений, принимаемых в ситуациях, содержащих элемент риска; вероят­ность таких исхо­дов описывается некоторым распределением изP. В за­висимости от контекста распределения изP называютставками,игра­ми,лотереями,альтернативамириска,смешаннымистратегиямиилирандомизи­ро­ванными стратегиями.

Для любых распределений p и q из P выражение p+(1-)q назы­вается прямой линейной комбинацией распределений p и q; где- дейст­вительное число и 0≤α≤1 . Еслиr=α·p+(1-α)·q, то для любогоxизXr(x)= α·p(x)+(1-α)·q(x). Еслии 0≤α≤1, то.

Пример

Пусть элементами Xявляются некоторые суммы денег и пусть

p(0)=0,3;p(10)=0,2;p(20)=0,5;q(7)=0,7;q(10)=0,3;=0,5 иr=α·p+(1-α)·q,

тогда r(0)=0,15;r(7)=0,35;r(10)=0,25;r(20)=0,25.

Аналогично рассмотренному ранее и на множестве P можно ввес­ти от­но­шение предпочтения  и функцию полезности. Так, например, ве­щес­твенная функцияu, заданная на множествеP, является функцией по­лезности для от­но­ше­ния, еслидля всех.

В рассматриваемом случае наличие определенных структурных свойств у множества Pприводит к тому, что функция полезностиuобла­дает свойством линейности, т.е.

u(α·p+(1-α)·q)= α·u(p)+(1- α)·u(q) (1)

для всех 0≤α≤1 и для всехpиq, принадлежащихP.

Функция полезности u, определенная для отношения наP, на­зы­ваетсялинейной функцией полезности, если для нее выполняется ра­вен­ство (1). Аналогично, еслиu- совершенная функция полезности, ко­то­рая удовлетворяет условию (1), то она на­зы­ваетсясовершеннойлинейной функцией полезности.

На основе функции полезности u, определенной для отношения наP, введем вспомогательную функциюvнаX

v(x)=u(p), когдаp(x)=1. (2)

Определим отношение предпочтения наXтак, чтотогда и толь­ко тогда, когдапри p(x)=1 и q(y)=1. В этом случаеvбу­дет функ­цией по­лезности для отношениянаXпри условии, чтоuяв­ляется функцией по­лез­ности для отношения наP.

Пусть - различные элементы множестваXи

.

Считая uлинейной функцией полезности, можно получить

. (3)

Согласно этому выражению, полезность pравна математи­чес­ко­му ожи­да­нию дополнительной функцииvс распределением вероятностейp, заданном наX.

Если рассматривать v(x)как полезность исхода, то выражение (3) озна­ча­ет, что полезность некоторой альтернативы (с элементом риска) рав­на ожи­дае­мой полезности для исходов, которые могут иметь место при использовании этой альтернативы.

Соотношение (3) очень важно, так как его можно использовать при мас­шта­бировании и вычислении полезности. Если функция v(x)опре­де­ле­на наXи масштабирована таким образом, что это согласуется с ус­ло­вием линейности и выражением (2), то с помощью равенства (3) мож­но вычислить функциюu(p)для любогоpиз множестваP.

Пусть отношение наPявляется слабым упорядочением,иu- совершенная линейная функция полезности. В этом случае значе­ние любого (одного) из элементовv(x),v(y)иv(z), например,v(y), можно однозначно вы­ра­зить через два других, если определить значение, при которомyнаходится в отношении безразличия к лотереи, имею­щей исходxс вероятностьюи исходzс вероятностью(1-) . Пусть та­ким значением является, тогда

. (4)

Следует отметить, что в реальной ситуации психологические осо­бен­­ности человека могут сделать поставленную задачу достаточно слож­ной, так как ока­зы­вается трудно определить точное значение , при ко­то­ромyнаходится в отношении безразличия к лотереи.

Пусть u- совершенная линейная функция полезности для отно­ше­ниянаP. Тогдатакже является совершенной линейной функ­цией полезности для отно­ше­ния наPтогда и только тогда, когда су­щест­вуют действительные числаb>0 и cтакие, чтодля всехp из P, т.е.иu связаны аффинным (линейным) положитель­ным (возрастающим) преобразованием.

Следует отметить, что при этом при всехx из X.

Итак:

1. если x и y - два элемента множества Xтакие, что, тоv(x)иv(y)могут быть любыми двумя числами, удовлетворяющими условию;

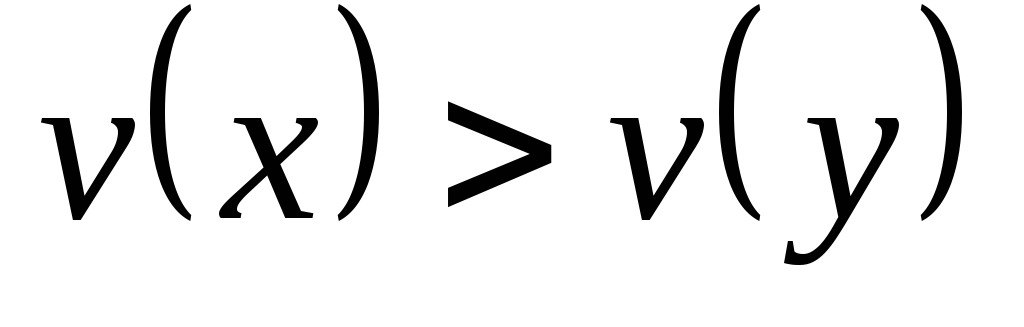2. для данных v(x)иv(y)значениеv(z)однозначно определяется из уравнения (4) для каждогоzиз X.

Определив таким образом функцию vнаX, можно полностью построить совершенную линейную функцию полезностиuнаP, вы­чис­лив ее с помощью соотношения (3).