Итерационный метод решения игр

Рассмотрим один из наиболее простых итерационных методов решения игр – метод Брауна - Робинсона. Основная идея метода заклю­чается в том, что игроки при многократном повторении игры при выборе стратегии в каждой конкретной партии используют весь накопленный в предыдущих партиях опыт.

Пусть - множество чистых стратегий игрокаА, а- множество чистых стратегий игрокаБ. Соответственно назо­вемэмпирическими смешанными стратегиямиигроковАиБпосле проведенияkпартий векторы

и ,

где - частота использования стратегийвkпар­тиях, а- соответственно число использования стратегийвkпартиях.

Алгоритм построения решения заключается в том, что разыгры­ва­ет­ся боль­шое число партий, причем в каждой партии каждый игрок вы­би­рает такую чистую стратегию, которая обеспечивает наилучший ре­зуль­тат для эмпи­ри­чес­кой смешанной стратегии, использованной против­ни­ком в предыдущих пар­тиях. После каждой партии значенияипе­ре­считываются (так как изме­ня­ет­ся число сыгранных партийk). Выбор игроками стратегий в первой партии произволен, например, можно ис­пользовать минимаксные стратегии.

Доказано, что

и ,

где и- оптимальные стратегии игроковАиБсоответственно, а выиг­рыш игрокаБ(проигрыш игрокаА) стабилизируется и стремится к цене игры.

При практической реализации метода вычисления прекращаются, когда

,

где ε- заданная точность.

При использовании метода Брауна - Робинсона следует иметь в виду, что он сходится медленно, но прост в реализации на ЭВМ, причем уве­личение раз­мер­ности игры не приводит к ощутимому увеличению объ­ема вычислений, чего нельзя сказать о методе сведения к задачам линейного программирования.

Лекция №11 Игры двух лиц с ненулевой суммой

В играх двух лиц с ненулевой суммой есть одна существенная осо­бенность: то, что хорошо для одного игрока, не обязательно плохо для другого. Следовательно, интересы не являются полностью противопо­ложными, и они могут извлечь выгоду из сообщения о своей стратегии. Различают два варианта таких игр:

1. некооперативные(бескоалиционные) игры, когда запреще­ны любые соглашения, обмен информацией, побочные плате­жи и совместный выбор стратегий;

2. кооперативныеигры, в которых разрешается любой вид кооперации.

В некооперативных играхзадают две функции выигрышаА(σ,τ)иВ(σ,τ), определенные для всех пар стратегий(σ,τ)и соответствующие выиг­ры­шам игроковАиБ. Если множества стратегий конечные, то функции выиг­ры­шаА(σ,τ)иВ(σ,τ)можно представить в виде матрици. Игра в такой форме называетсябиматричной игрой.

В общем случае в таких играх равновесных пар чистых стратегий может и не существовать, но справедливо следующее утверждение.

Теорема.В любой биматричной игре существует, по крайней мере, одна равновесная пара смешанных стратегий.

К сожалению, для игр с ненулевой суммой равновесные пары не полнос­тью удовлетворяют понятию «решение игры». Рассмотрим при­ме­ры, которые демонстрируют соответствующие трудности.

Пример 1

Фирма Аможет выпускать два сорта кофе: дешевый и доро­гой, а фирмаБ- два типа кофейников: дешевые и дорогие. Дорогой кофе можно сварить в любом кофейнике, а дешевый кофе – только в дорогом кофейнике.

Если одна фирма производит дорогой продукт, а другая – деше­вый, то существуют соизмеримые объемы продажных товаров, при кото­рых фирма, выпускающая дорогой продукт, получит большую прибыль, а другая будет иметь некоторую разумную прибыль. Если обе фирмы бу­дут выпускать дорогую продукцию, то объемы продаж будут малы и ни одна из них не получит никакой прибыли. Если же обе фирмы будут выпускать дешевую продукцию, то они ничего не продадут.

Рассматриваемую игру, разумным образом вводя полезность (в ус­лов­ных единицах), можно представить с помощью двух матриц

.

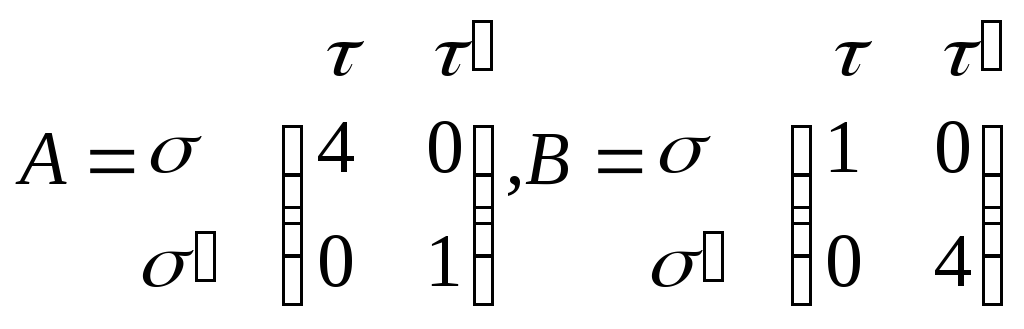Нетрудно видеть, что равновесными будут пары и. Однако парыине являются равновесными. Более того, выигрыши в равновесных точках различны.

Пример 2 (дилемма заключенного)

Два преступника ожидают приговора суда за совершенное злодея­ние. Ад­вокат конфиденциально предлагает каждому из преступников об­лег­чить его участь (и даже освободить!), если он сознается и даст по­ка­за­ния против сообщ­ника. Если никто не сознается, то обоим угрожает за­клю­чение на определен­ный срок по сфабрикованному обвинению в не­зна­чительном преступлении.

Каждый заключенный имеет на выбор две стратегии: не соз­на­вать­ся или сознаться, выдав при этом сообщника. Разумно назна­чив полезность, можно получить матрицы

.

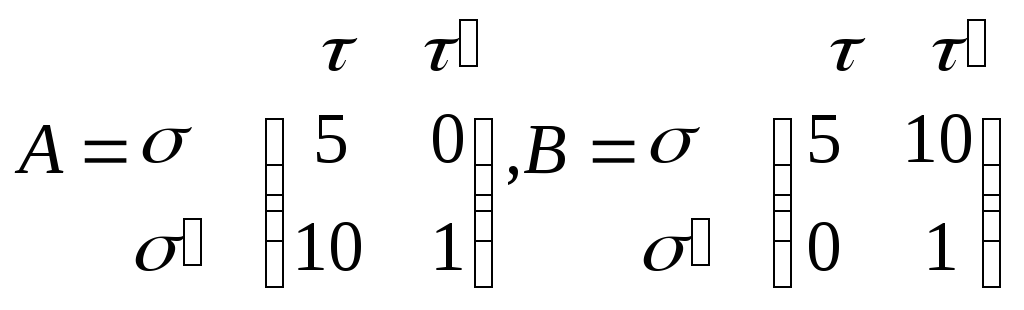Нетрудно видеть, что - единственная равновесная пара, од­на­ко неравновесные стратегии дадут им больший выигрыш.

Рассмотренные примеры показывают, что некооперативные игры двух лиц с ненулевой суммой существенно отличаются от игр двух лиц с нулевой сум­мой. Подробнее остановиться на таких играх не позволяет объем нашего курса.

В основе кооперативных игрлежит предпосылка, согласно кото­рой оба игрока могут в целом достичь большего, если будут действовать сообща, - в этом и состоит ценность кооперации. Такая кооперация, ес­тественно, должна оплачиваться, что приводит к различнымсделкам, или так называемымпобочным платежам.

В простейшем случае предполагается, что два игрока не могут воз­действовать друг на друга, пока не придут к некоторому соглашению. Таким образом, игра определяется посредством подмножества Sв ев­кли­довом пространстве, представляющего (общие) выигрыши, которые оба игрока могут получить в слу­чае кооперации; кроме того, заданы два числа, определяющие вели­чи­ну выигрыша каждого из игроков без кооперации между ними.

Обычно предполагают, что подмножество S является замкнутым, выпук­лым и ограниченным сверху (в том смысле, что для любых(a,b)мно­жество всехсограничено). В таком случае, ос­но­вываясь на разумной системе аксиом (аксиомах Нэша), можно прий­ти к выводу, что игроки «должны» согласиться получить выигрыш, соот­ветст­вующий точке, в которой достигается

при ограничениях .

Такая точка известна какточка Нэша. Можно доказать, что она единственна.

В более общем случае каждый из игроков может воздействовать на другого, даже если соглашение между ними не достигнуто. В этом слу­чае игра будет иметь более сложную структуру, определяемую множест­вом S, аналогичным введенному выше, и двумя функциями платежейА(σ,τ)иВ(σ,τ), которые характеризуют выигрыши игроков, если они не могут достичь соглашения (здесьσиτ– стратегии двух игроков).

Идея состоит в том, что стратегии σиτвыбираются и исполь­зуются какугроза, которая осуществляется только в том случае, если соглашение не достигнуто. Тогда сделка может быть заключена, если каждый из игроков знает угрозу другого. Последнее обстоятельство при­водит к тому, что исход сделки будет зависеть от весомости угроз.

Если сделаны угрозы σиτ, то исходом сделки должна быть точка, в которой достигается

при ограничениях .

Таким образом, точка логически получается в результате приме­не­ния пары угроз. При этом появляется возможность опре­де­лить равно­вес­ную паруне через выигрыши (с угрозой!)А(σ,τ)иВ(σ,τ), а скорее через логические исходы.

Относительно введенных понятий верна следующая теорема.

Теорема. Если множества стратегий обоих игроков конечны, то су­щест­вует по крайней мере одна равновесная пара смешанных стратегий угроз, которая известна как оптимальная стратегия угроз.

Эта теорема гарантирует существование значений и опти­маль­ных угроз для конечных игр. Конечно, вычислить их весьма сложно, так как они за­ви­сят от обеих платежных матрицА,Ви от множестваS.