Алгебраическое представление графа

Помимо графического и теоретико-множественного часто исполь­зуют и алгебраическое представлениеграфа в виде матрицы.

Рассмотрим орграф G, содержащийnвершин иmребер.Мат­ри­цей смежностиорграфаG называется матрицаA размераnn

,

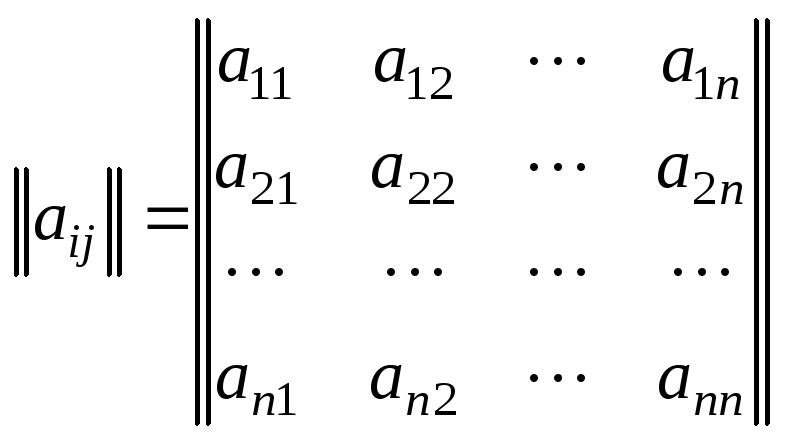где

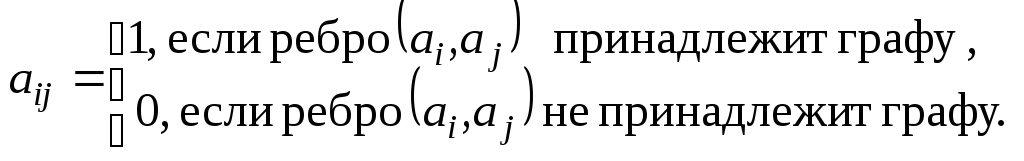
Иногда матрицу смежности называют матрицей отношений, или матри­цей не­пос­ред­ст­вен­ных связей.

Матрицей инцидентности(илиматрицей инциденций) орграфаGна­зы­вается матрицаB размераnm, у которой

Для введения матрицы смежности нужно пронумеровать вершины, а для матрицы инцидентности - и ребра графа.

Алгебраическое представление позволяет алгоритмизировать в удоб­ной для программи­рования на ЭВМ форме процедуру определения структурных количественных параметров системы.

Рассмотрим теперь некоторые методы решения практических за­дач, ис­пользуя введен­ный нами математический формализм.

Лекция №3 Ранжирование элементов систем

Анализ связей в графе заключается, прежде всего, в нахождении и оцен­ке путей между его верши­на­ми. Помимо непосредственного отыс­ка­ния пу­ти в не­ко­торой системе коммуникаций к этой задаче относится, например, задача вы­бора опти­маль­ной стратегии и др. Действительно, достаточно вершинам графа по­ста­вить в соответствие некоторые цели, а длинам путей - стоимости дос­ти­жения этих целей, чтобы получить за­да­чу выбора стра­те­гии дости­же­ния цели с наименьшими издержками.

Поиски путей по чертежу при сколько-нибудь сложной структуре гра­фа (на практике приходится анализировать графы с числом вершин более 100) за­труд­нены и сопряжены с возможностью ошибок. Поэтому рас­смотрим один из алгебраических методов, удобный для использова­ния ЭВМ. Этот метод поз­во­ля­ет, исходя из матрицы непосредственных связей , построитьполную матрицу путей, где- число путей из вершиныiк вершинеj(= 0), либо ограничиться отысканием од­но­го из ее элементов.

Числа или их буквенные выражения определяются при помо­щи опре­де­лителей особого рода -квазиминоров(беззнаковыхопре­де­ли­те­лей). Имеет место формула

.

Выражение называютквазиминором элементамат­ри­цы. Знакявляется символом квазиминора, аука­зы­вает на матрицу с вычеркнутымиl-й строкой иk-м столбцом, ко­то­рая впи­сывается в символ квазиминора подобно матрице, вписываемой в сим­вол обычного минора.

Вычисление квазиминора сводится к разложению его на квазими­но­ры меньшего порядка по формуле

Здесь

Процедура вычисления во многом сходна с процедурой вычис­ле­ния обыч­ных определителей, но для овладения этим методом требуется не­ко­то­рый навык.

Пример.

Пусть матрица непосредственных связей имеет вид

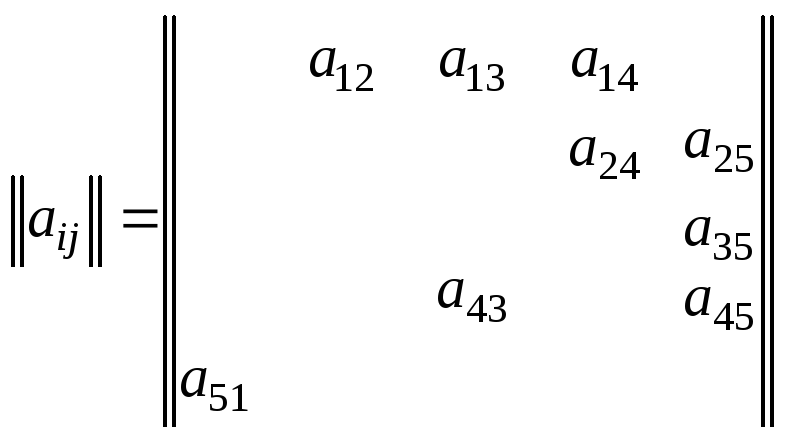
Необходимо найти все пути, ведущие из вершины 1 в 5, и подсчи­тать их число.

Для рассматриваемого примера получаем

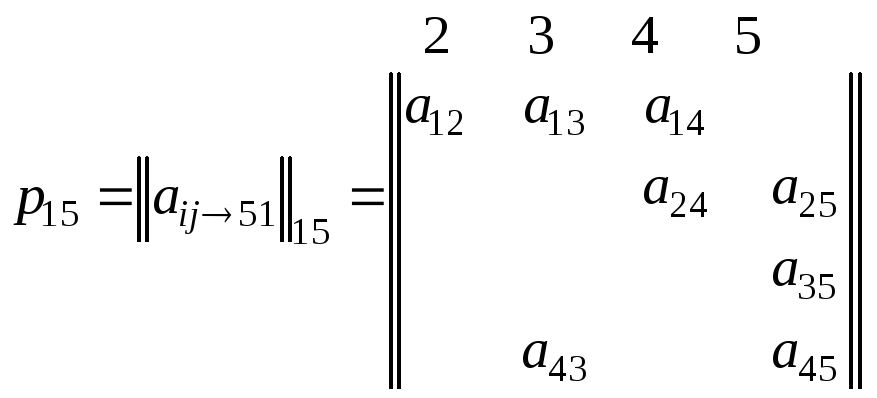
Первоначально в матрице вычеркивается столбец 1, соответ­ст­вую­щий номеру вершины, от которой начинается путь, и строка 5, соот­вет­ст­вующая номеру вершины, в которой путь заканчивается. Это соот­вет­ствует удалению из графа всех ребер, ведущих в вершину 1 и выхо­дя­щих из вершины 5. По­ло­же­ние и нумерацию остальных строк и столб­цов удобнее оставить без из­ме­нения. Далее необходимо про­из­вес­ти раз­ло­жение полученного квази­ми­но­ра по ненулевым элементам 1-й строки

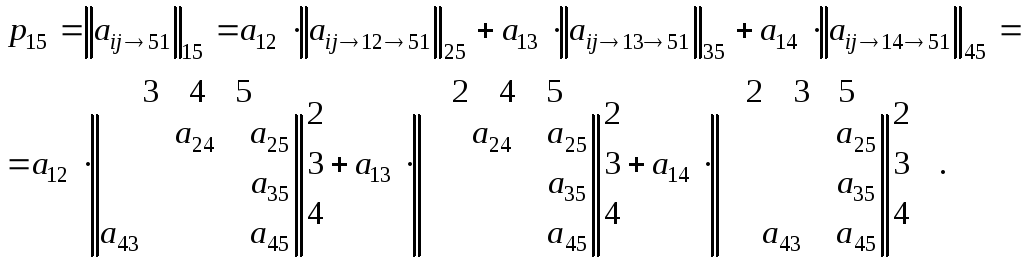
Разложение для первого слагаемого ведется по второй строке, вто­ро­го - по третьей, третьего - по четвертой, т.е. номер стро­ки, по которой ведется разложение, равен номеру столбца, в ко­то­ром на­хо­дился последний член разложения.

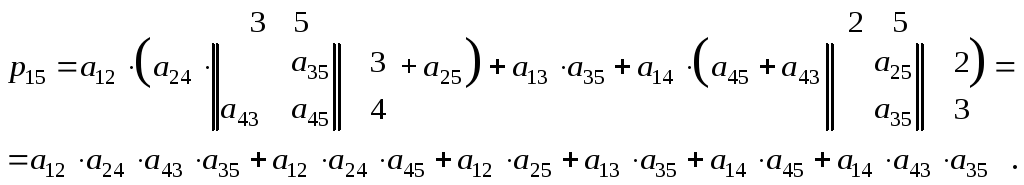
Если теперь положить для ненулевых элементов = 1 и про­из­вес­ти опе­ра­ции по правилам обычной арифметики, то получим количество пу­тей из вер­ши­ны 1 в вершину 5 -.

Если же в полученном выражении произвести действия по пра­ви­лам буле­вой алгебры, то получим значение полной матрицы связей, которая ха­рактеризуетсвязность графа. Значения элементов пол­ной мат­рицы связейопределяются так:

= 1, если вершина i связана с вершиной j хотя бы одним путем,

=0 в противном случае.

Обычно считают, что .

Связность - важнейшая характеристика структурной схемы систе­мы. Струк­тура тем луч­ше, чем полнее заполненность полной матрицы связей. На­ли­чие большого числа нулей гово­рит о серьезных изъянах в структуре системы.

Другая важная характеристика структуры - распределение значи­мо­с­ти эле­мен­тов сис­те­мы. Количественная характеристика значимости - ранг элемента- впервые явно была сфор­му­лирована при анализе струк­ту­ры отношений домини­ро­вания (превосходства, преобладания) в груп­пах индивидуумов (людей, жи­вот­ных).

Используя полную матрицу путей , значения рангов элемен­тов опре­де­ляются по формуле

.

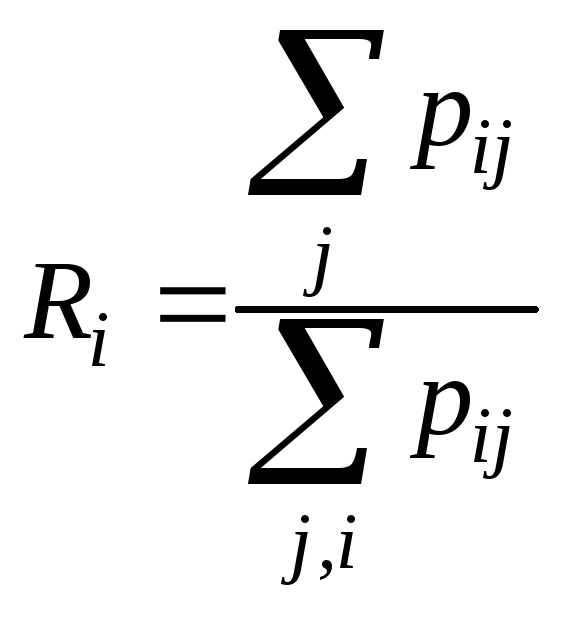Следует иметь в виду, что значимость элемента определяется не са­мим значением , а сравнением рангов всех элементов, т.е. ранг- это от­но­си­тельный показатель значимости.

Какие же практические рекомендации можно выработать, проведя ранжи­ро­вание элементов системы?

Чем больше ранг данного элемента, тем большим числом путей он связан с другими элементами и тем для большего числа элементов нару­шат­ся нор­маль­ные условия работы при его отказе. Следовательно, при формировании про­граммы обеспечения надежности рассмат­ри­ваемой сис­те­мы необходимо уделить особое внимание элементам с большим рангом.

Для систем со структурой типа сетей наличие элементов с ран­га­ми, заметно боль­ши­ми, чем у остальных, обычно свидетельствует о функ­­циональной перегрузке этих элементов. Желательно перераспре­де­лить связи, преду­смот­реть обходные пути, чтобы уравнять значи­мость эле­ментов данной системы.

Существуют и другие методики определения рангов. Выбор под­хо­дя­щей методики опре­деляется спецификой задачи.

Следует отметить, что имеются структуры, ранжирование элемен­тов кото­рых может потерять практический смысл. Это, прежде всего, иерар­хи­ческие струк­туры. Значимость элемента в них определяется уров­нем иерар­хии.