надежность машин и оборудования

	161
	Пример 8.25. Коэффициент вариации ресурса дви-				Таблица 8.22
	гателей определенной марки равен 0,4. При испытани-
		ЗНАЧЕНИЯ КОЭФФИЦИЕНТА C
	ях 12 двигателей в течение 3000 ÷ два двигателя ис-
	черпали ресурс. Определить оценки 80%-ного и сред-
		v	0,3	0,4		0,6	0,8
	него ресурсов.
		c	1,35	1,56		2,14	3,06
	Äëÿ v=0,4, N=12 è r=2 значение коэффициента

k=1,08 (прил.I). По формуле (8.101) оценка 80%-ного ресурса двигателей T0,8* = 1,08×3000=3240 ÷.

Äëÿ v=0,4 значение коэффициента ñ=1,56 (табл.8.22). По формуле (8.103) оценка среднего ресурса двигателей T* = 1,56×3240 » 5050 ÷.

Пример 8.26. Наблюдения проводились за 26 тракторами. Наработки тракторов

незначительно отличались между собой, средняя наработка составила 2600 ÷. На двух тракторах муфта сцепления исчерпала ресурс, на остальных ее ресурс не был исчерпан. Коэффициент вариации ресурса муфты равен 0,3. Определить оценки 80%-ного и среднего ресурсов муфты сцепления.

Èç ïðèë.I äëÿ v=0,3, N=26 è r=2 значение k = 1,32. Оценка 80%- ного ресурса муфты сцепления по формуле (8.101) T0,8* =1,32×2600 » 3430 ÷.

Äëÿ v=0,3 значение коэффициента ñ=1,35 (табл.8.22). По формуле (8.103) оценка среднего ресурса муфты сцепления T* = 1,35×3430 » 4630 ÷;

Пример 8.27. Испытывались 16 коробок передач. За период испытаний три коробки передач исчерпали ресурс при наработках 1000, 1200 и 2000 ÷. Из оставшихся пять

были сняты с испытаний при наработке 1200 ÷, восемь - при наработке 2300 ÷. Определить оценки 80%-ного и среднего ресурсов коробки передач, если известно, что коэффициент вариации ресурса равен 0,4.

Из рис.8.8 по коэффициенту вариации v=0,4 находим параметр формы распределе-

ния Вейбулла b =2,7. По формуле (8.100) определяем оценку 80%-ного ресурса коробки передач

				êé-	1	(10002,7		2,7 )úù	1
		= (- ln 0,8)	1
	T0*,8						+ 12002,7 + 20002,7 + 5 ×12002,7 + 8 × 2300		2,7	» 2048.
			2,7
					3
		ë						û

Äëÿ v=0,4 значение коэффициента ñ=1,56 (табл.8.22). По формуле (8.103) оценка среднего ресурса коробки передач T* = 1,56×2048 » 3190 ÷.

8.5.5. Расчет ресурса при отсутствии отказов

Если за время испытаний ни одно из изделий не отказало, то рассчи- тываются только нижние доверительные границы показателей надежности.

Нижняя доверительная граница гамма-процентного ресурса

					ln(g)	ù1b æ				1
				é				N	ö b
		T	g	= ê		ú	çç	åTib	÷÷	,	(8.104)
					ln(1 - g)
				ë		û	èi=1		ø

ãäå T1,T2,...,TN - наработки изделий к окончанию испытаний; b - параметр формы распределения ресурса по принятому значению коэффициента вариации v (ðèñ.8.8).

В случае усеченных испытаний, когда все изделия испытываются до одной наработки T, формула (8.104) принимает вид

1

é N ln(g) ùb

T g = ê ( ) ú T = DT, (8.105)

ëln 1 - g û

ãäå D - коэффициент, зависящий от числа изделий N, коэффициента формы b и значе- ния g.

Нижняя доверительная граница среднего ресурса определяется по формуле, аналогичной формуле (8.103):

T = ñT0,8,

(8.106)

в которой коэффициент с находится по табл.8.22.

162

Пример 8.28. Наработки 20 тракторов за период наблюдений незначительно отли-

чились между собой и средняя наработка составила 3000 ÷. Ни на одном из тракторов задний мост не исчерпал ресурс. Определить нижние доверительные границы для 80%- ного и среднего ресурсов при доверительной вероятности 0,8. Коэффициент вариации ресурса равен 0,4.

По рис.8.8 при коэффициенте вариации ресурса v=0,4 параметр формы распределения Вейбулла b=2,7. В формуле (8.105) D = (20×ln0,8/ln0,2)1/2,7 = 1,46 и нижняя до-

верительная граница 80%-ного ресурса T0,8 = 1,46×3000=4380 ÷.

Ïî òàáë.8.22 ïðè v=0,4 коэффициент c=1,56 и по формуле (8.106) нижняя оценка среднего ресурса T = 1,56×4350 » 6790 ÷.

Пример 8.29. Наблюдались 15 тракторов, из них пять - до наработки 2000 ÷ è äå-

сять - до наработки 3000 ÷. Ни на одном из тракторов конечные передачи не исчерпали ресурс. Определить нижнюю доверительную границу 80%-ного ресурса конечных передач при доверительной вероятности 0,8, если известно, что коэффициент вариации их ресурса равен 0,4.

По рис.8.8 при коэффициенте вариации v=0,4 параметр b=2,7. По формуле (8.104) нижняя доверительная граница 80%-ного ресурса

						1		1
			æ ln 0,8ö 2,7
							(5 × 20002,7 + 10 × 30002,7 )2,7
	T	0.8	= ç		÷				» 3586.
			è ln 0,2ø
По формуле (8.106)				нижняя			оценка среднего ресурса		конечных передач T =

1,56×3586 » 5590 ÷.

8.5.6. Расчет среднего числа отказов за установленную наработку

Среднее число отказов за установленную наработку рассчитывается либо по машине в целом, либо по отдельным агрегатам. Расчет проводится отдельно по каждой группе сложности отказов.

Максимальная из наработок машин tmax разбивается на 10 интервалов t=tmax/10, при этом нижняя граница j-го интервала равна (j−1)tmax/10, верхняя - jtmax/10. Для каждого интервала подсчитывается условное чис-

ло машин, работавших в этом интервале Nj:

	rj	τ	ij
Nj	= å			,	(8.107)
			t
	i=1

ãäå rj - число изделий, отказавших в j-ом интервале; Dt - величина интервала наработки; tij - наработка i-го изделия в j-м интервале (если изделие в интервале не отказало,

òî tij = Dt).

Среднее число отказов одного изделия в j-ом интервале

mj = rj/Nj,	(8.108)
среднее число отказов за назначенный период работы	(за наработку
jtmax/10)
j
Mj = åmk .	(8.109)
k=1
Параметр потока отказов в i-ом интервале
ωj = mj/ t.	(8.110)

Если значение tmax меньше назначенной наработки Tí, на которую необходимо провести прогноз, то прогнозирование среднего числа отказов по разным группам сложности агрегата за эту наработку проводится следующим образом. Когда для какой-то группы сложности отказы наблюдаются не более чем в одном интервале наработки или не наблюдаются ни в од-

163

ном из интервалов, кроме трех последних, тогда прогнозируемое среднее число отказов mïð определяется по формуле

mïð(Tí) = Tí×M/tmax. (8.111)

Во всех остальных случаях, если отказы наблюдались хотя бы в двух интервалах наработки и хотя бы в одном из первых семи интервалов, то среднее число отказов за назначенный период работы аппроксимируется степенной функцией

m T	=	ì0, ï ðè			Tí < c,				(8.112)
ï p( í )		í		)	b		í
		î ( í	- c			, npu		³ c,
		a T					T

ãäå c - нижняя граница первого интервала наработки, в котором наблюдались отказы данной группы сложности; a è b - постоянные:

ln a =	åln miåln2(ti - c) - åln(ti - c)åln mi × ln(ti - c)
		nåln2(ti	- c) - [åln(ti - c)]2
			(8.113)
	b =	nåln miåln(ti - c) - åln miåln(ti - c)
		nåln2	(ti - c) - [åln(ti - c)]2

где суммирование производится по всем интервалам наработки, в которых mi ¹ 0.

Åñëè tmax > Òí, то берется интервал наработки, концы которого удовлетворяют неравенству tj−1£ Tí £ tj. В этом случае прогнозируемое число отказов за наработку Tí определяется линейной интерполяцией:

m T	= m	j-1	+	TH − tj-1	m	.	(8.114)
ïð( í )				Dt	j

Пример 8.30. Необходимо определить среднее число отказов второй группы сложности отремонтированного

трактора за 3000 ÷, если в эксплуатации получены следующие данные (см.табл.8.23):

Среднее число отказов за 1200 ч по формуле (8.109):

			Таблица 8.23
ЭКСПЛУАТАЦИОННЫЕ ДАННЫЕ ТРАКТОРОВ
Номер	Интервал	Число машин	Число отказов
интервала	наработки, ÷.	в интервале	в интервале
1	äî 200	15	6
2	200-400	15	7
3	400-600	12	8
4	600-800	9	4
5	800-1000	3	2
6	1000-1200	2	1

M(1200) = 156 + 157 + 128 + 94 + 23 + 12 = 314, .

Принимая tmax= 1200 ÷, определяем среднее число отказов за назначенную наработку Tí = 3000 ÷ по формуле (8.111):

mïð(3000) = 12003000 × 314, = 7,85.

Если информация об отказах за период испытаний (наблюдений) недостаточна для оценки характеристик ресурса, то необходимо дополнительно использовать данные диагностики об отклонении параметров технического состояния от номинальных значений. По этим данным определяются полные и остаточные ресурсы элементов, которые затем вместе с данными о наработках отказавших одноименных элементов обрабатываются как полная выборка.

164

Ëè ò å ð à ò ó ð à

1.Канарчук В.Е. Основы надежности машин.- Киев: Наукова думка, 1982.- 248 с.

2.Кугель Р.В. Испытания на надежность машин и их элементов.- М.: Машиностроение, 1982.- 181 с.

3.ÃÎÑÒ 16504-81. Система государственных испытаний продукции. Испытания и контроль качества продукции. Основные термины и определения.

4.ÃÎÑÒ 28.001-76. Система технического обслуживания и ремонта техники. Основные положения.

5.ÃÎÑÒ 21623-76. Система технического обслуживания и ремонта техники. Показатели для оценки ремонтопригодности. Термины и определения.

6.Надежность и эффективность в технике: Справочник: В 10 т. Т.1. Методология, организация, терминология. - М.: Машиностроение, 1986.- 224 с.

7.Сотсков Б.С. Основы теории и расчета надежности элементов и устройств автоматики и вычислительной техники.- М.: Высш.школа, 1970.- 272 с.

8.Надежность и эффективность в технике: Справочник: В 10 т. Т.6. Экспериментальная отработка и испытания. - М.: Машиностроение, 1989.- 376 с.

9.Надежность технических систем. Справочник. Под ред. И.А.Ушакова.- М.: Радио и связь, 1985. - 608 с.

10.Фишбейн Ф.И. Методы оценки надежности по результатам испытаний.- М.: Знание, 1973.- 98 с.

11.ÃÎÑÒ 27.002-89. Надежность в технике. Термины и определения.

12.Аронов И.З., Бурдасов Е.И. Оценка надежности по результатам сокращенных испытаний.- М.: Изд-во стандартов, 1987.- 184 с.

13.ÃÎÑÒ 27.504-87. Надежность в технике. Методы оценки показателей надежности по цензурированным выборкам.

14.Гнеденко Б.В., Беляев Ю.К., Соловьев А.Д. Математические методы в теории надежности.- М.: Наука, 1965.- 524 с.

15.Введение в теорию порядковых статистик.- М.: Статистика, 1970.- 414 с.

16.ÃÎÑÒ 27.503-87. Надежность в технике. Система сбора и обработки информации. Методы оценки показателей надежности.

17.Гребеник В.М., Цапко В.К. Надежность металлургического оборудования. Справочник.- М.: Металлургия, 1980.- 344 с.

18.Хазов Б.Ф., Дидусев Б.А. Справочник по расчету надежности машин на стадии проектирования.- М.: Машиностроение, 1986.- 224 с.

19.Бессонов А.А., Мороз А.В. Надежность систем автоматического регулирования.- Л.: Энергоатомиздат, 1984.- 216 с.

20.Вентцель Е.С., Овгаров Л.А. Теория вероятностей.- М.: Наука, 1973.- 260 с.

21.Капур Е., Ламберсон Л. Надежность и проектирование систем.- М.: Мир, 1980.- 604 с.

22.Хан Г., Шапиро С. Статистические модели в инженерных задачах. - М.: Мир, 1969.- 396 с.

23.Химмельблау Д. Анализ процессов статистическими методами. - М.: Мир, 1973.- 958 с.

24.Сотсков Б.С. Основы теории и расчета надежности элементов и устройств автоматики и вычислительной техники.- М.: Высш.шк., 1970.- 272 с.

25.Справочник по надежности. Том 1.- М.: Мир, 1969.- 340 с.

26.Труханов В.М. Методы обеспечения надежности изделий машиностроения.- М.: Машиностроение, 1995.- 304 с.

27.Королев В.Л. Основы испытаний на надежность. Учебное пособие.- Красноярск: КГТУ, 1997.- 126 с.

28.Ллойд Д., Липов М. Надежность: организация, исследования, методы, математический аппарат.- М.: Сов.радио, 1964.- 686 с.

29.Беляев Ю.К. Непараметрические методы в задачах обработки результатов испытаний и эксплуатации.- М.: Знание, 1984.- 65 с.

30.Скрипник В.М., Назин А.Е. Оценка надежности технических систем по цензурированным выборкам.- Минск: Наука и техника, 1981.- 143 с.

31.Статистические задачи отработки систем и таблицы для числовых расчетов показателей надежности. Под ред.Р.С.Судакова.- М.: Высш.школа, 1975.- 604 с.

32.Судаков Р.С. Испытания систем: выбор объемов и продолжительности.- М.: Машиностроение, 1988.- 445 с.

165

Г л а в а 9

КОНТРОЛЬНЫЕ ИСПЫТАНИЯ НА НАДЕЖНОСТЬ

Как уже отмечалось, целью контрольных испытаний на надежность (или контроля показателей надежности по альтернативному признаку) является проверка соответствия фактического уровня надежности партии требованиям, установленным в нормативно-технической документации [1- 3]. По результатам испытаний партия объявляется либо годной, либо браком. Это утверждение принимается на основании экспериментального исследования части партии (выборки).

В процессе разработки изделия контроль надежности проводится как минимум один раз на приемочных испытаниях. При серийном производстве контроль надежности производится периодически. Для малосерийных высоконадежных изделий контроль надежности вводится в состав типовых испытаний, проводимых при изменениях в конструкции, технологии или составе комплектующих. Основанием для проведения контрольных испытаний могут быть также сведения о недостаточном уровне надежности, полученные в результате каких-либо других испытаний или эксплуатации. Контроль надежности больших сложных систем с широким применением резервирования может быть включен в состав приемо-сдаточных испытаний.

Изделия, образующие партию объема N, характеризуются некоторым показателем надежности R. При контрольных испытаниях может исследоваться время безотказной работы, продолжительность восстановления и т.п., отрицательным исходом наблюдения будет наступление отказа или предельного состояния, невозможность восстановления в течение заданного времени и т.п. Соответственно уровень надежности может контролироваться по значениям вероятностей безотказной работы (или отказа), безотказного хранения, восстановления и т.п. (показатели типа вероятности P) или наработки, ресурса, срока службы, срока сохраняемости, срока хранения, времени восстановления и т.п. (показатели типа наработки T) [4].

Совокупность случайных значений параметра R во всей партии называется генеральной совокупностью, а его среднее значение - соответственно генеральным или фактическим Rô значением параметра в партии. Для генерального параметра Rô устанавливаются два уровня: R0, соответствующий нормальному уровню надежности, и R1, соответствующий минимально допустимомой надежности. В зависимости от соотношения генерального параметра Rô с заданными уровнями R0 è R1 партия квалифицируется по следующим неравенствам:

Rô ³ R0,

Rô £ R1,

R1 < Rô < R0 .

(9.1)

В первом случае партия должна приниматься (годная партия), во втором - браковаться (негодная партия), в третьем случае партию допускается и принять и забраковать (допустимая партия).

166

Неравенства (9.1) соответствуют случаю, когда в качестве показателя надежности R используются показатели, большие значения которых характеризуют большую надежность (средняя наработка Tñð, вероятность безотказной работы p(t) и т.д.). Для показателей, большие значения которых характеризуют меньшую надежность (например, вероятность q(t)

или интенсивность отказов l), в соотношениях (9.1) изменятся знаки неравенств.

Таким образом, в ходе испытаний нужно проверить и выбрать одну из двух взаимоисключающих гипотез:

- прямая гипотеза H0 - надежность партии соответствует требовани-

ÿì: Rô ³ R0;

- обратная (альтернативная) гипотеза H1 - надежность партии не

соответствует требованиям: Rô £ R1.

Третий возможный исход (9.1) "допустимая партия" в зависимости от условий может быть присоединен к любому из утверждений H0 èëè H1.

Испытаниям подвергается, как правило, часть партии объемом n (выборка). Значения параметра R изделий в выборке образуют выборочную совокупность, характеризуемую некоторым выборочным распределением f(R). При контроле надежности невосстанавливаемых изделий объем выборки равен необходимому количеству наблюдений, для восстанавливаемых изделий объем выборки может быть уменьшен вплоть до одного образца, если обеспечивается независимость наблюдений к началу очередного наблюдения [4]. Среднее значение параметра надежности R в выбороч- ной совокупности R* называется выборочным, и оно может быть вычислено по результатам экспериментальных исследований выборки.

Выбор одной из гипотез H0 èëè H1, наиболее соответствующей выборочной совокупности, производится по определенным правилам - критериям проверки гипотез, которые и определяют метод контроля надежности - одноили двухступенчатый, последовательный и др.

Основные методы статистического контроля показателей надежности по альтернативному признаку регламентируются в ГОСТ 27.410-87 [4].

9.1. Метод одноступенчатого контроля

Одноступенчатый контроль надежности (метод однократной выборки) сводится к организации и проведению наблюдений некоторого объема n с фиксацией набора результатов наблюдений R1,R2,...,Rn. По окончании наблюдений вычисляется некоторая функция результатов наблюдений R*(R1,R2,...,Rn), область определения которой разделена на две непересекающиеся области (R*<Rïð è R*>Rïð) и решение о приемке или браковке изделия принимается в зависимости от того, в какую из них попадает рас- четное значение R*[5].

Процедуре испытаний предшествует их планирование, заключающееся в нахождении значений приемочного норматива показателя Rïð и объема выборки n, удовлетворяющих заданным значениям рисков изготовителя a

167

и заказчика b, а также нормальному R0 и минимально допустимому R1 значениям генерального показателя R [1,3]. Выборка n изделий из партии подвергается испытаниям, по результатам которых вычисляется выбороч- ная точечная оценка R*. Ее сравнением со значением Rïð производится выбор гипотезы о приемке или браковке партии.

Существует несколько способов разделения выборочного пространства на две области с помощью различных функций R*(R1,R2,...,Rn), каждый из которых имеет свои достоинства и недостатки в зависимости от конкретных условий применения, однако наиболее часто используется критерий согласия Неймана-Пирсона, обеспечивающий при заданных условиях (уровнях риска изготовителя a и заказчика b) наименьший требуемый объем наблюдений n.

9.1.1. Критерий Неймана-Пирсона

Проверка гипотез по критерию согласия Неймана-Пирсона заключается в сравнении выборочной оценка R* с назначенным приемочнобраковочным нормативом Rïð. Ïðè R*³Rïð принимается гипотеза H0 (ò.å.

утверждается, что Rô ³R0), ïðè R*<Rïð принимается гипотеза H1 (Rô £R1). Из-за выбора гипотез по ограниченному объему статистических данных

(n<N) принципиально возможны ошибки двух видов.

Ошибка первого рода заключается в том, что по испытаниям выборки утверждается гипотеза H1 и партия бракуется, тогда как в действительности партия приемлема. Максимальная вероятность ошибки первого рода называется риском изготовителя (или поставщика) a [5]. Если обозна- чить через P1 вероятность браковки партии, то риск изготовителя можно определить как условную вероятность

a = max{P(R* < Rïð /Rô ³ R0)} = max{P(R* < Rïð /H0)} = max{P1(H0)}. (9.2)

Ошибка второго рода заключается в том, что по результатам испытаний выборки утверждается гипотеза H0 и партия принимается, тогда как в действительности партия неудовлетворительная. Максимальная вероятность ошибки второго рода называется риском заказчика (или потреби-

òåëÿ) b [5]. Обозначив через P0 вероятность приемки партии, риск заказ- чика можно определить как условную вероятность

b = max{P(R* > Rïð / Rô £ R1)} = max{P(R* > Rïð /H1)} = max{P0(H1)}. (9.3)

Очевидно всегда P0 + P1 = 1.

Ошибки при выборочных испытаниях неизбежны, однако их вероятность можно сделать сколь угодно малой. Величины P0 è P1 определяются значениями R* è Rïð - большие значения R* способствуют приемке партии. Поскольку выборка при испытаниях подбирается случайным образом, средний уровень надежности в ней определяется неизвестной генеральной характеристикой Rô. Зависимость P0 èëè P1 îò Rô называется оперативной характеристикой выборочного контроля надежности. Назначенное значение Rïð также влияет на исход испытаний: его увеличение способст-

		168
	P	P
	1
		1

	2	1
		Rïð1>Rïð2		n1<n2<n3=N
			1
	0		2	3
		Rô	0	Rïð	Rô
	Рис.9.1. Изменение оперативной		Рис.9.2. Изменение оперативной
	характеристики при изменении		характеристики при изменении
	приемочного уровня Rïð		объема выборки n
	(сплошные линии - P0, штриховые - P1)

вует браковке, а уменьшение - приемке. Изменение величины Rïð приводит к сдвигу оперативной характеристики по оси Rô (ðèñ.9.1).

Третьим фактором, определяющим вероятности приемки и браковки, является объем выборки n: чем он ближе к объему партии N, тем меньше элемент случайности в определении выборочной характеристики R* и, соответственно, в выполнении условий приемки или браковки. В пределе n=N случайность величины R* полностью исключается и кривая оперативной характеристики обращается в "ступеньку" (рис.9.2).

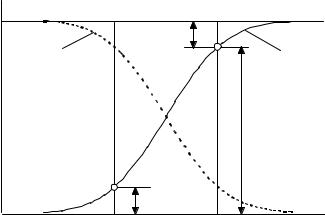
Очевидно, ошибочная приемка, т.е. ошибка второго рода, может произойти только в области значений Rô ≤ R1 (рис.9.3), так как согласно условиям (9.1) при больших значениях Rô приемка перестает быть ошибоч- ной. При этом вероятность ошибочной приемки максимальна при Rô=R1, следовательно, риск заказчика (9.3)

β = P0(Rô=R1).	(9.4)
Ошибка первого рода возможна только при Rô ≤ R0 и максимальна в
точке R0, так что риск изготовителя
α = P1(Rô=R0) = 1 – P0(Rô=R0).	(9.5)

Значения четырех величин R0, R1, α è β определяют две точки оперативной характеристики (рис.9.3) с координатами, соответственно, (R1,β) è

(R0,1−α) и, в свою очередь, позволяют составить план контроля надежности.

Вариацией величин n è Rïð можно получить кривую оперативной характеристики Ð0(Rô), которая обеспечит любые сколь угодно малые заданные значения α è β. Формально выражения (9.4) и (9.5) образуют систему уравнений, связывающих величины R0, R1, α, β, n è Rïð и позволяют вычислить n è Rïð, удовлетворяющие заданным α, β, R0 è R1. Эта процедура, называемая планированием проверки гипотез, является основной частью проверки по критерию Неймана-Пирсона.

169

Следует отметить, что в целом P

возможно вместо двух иметь один кри-

1

a

тический уровень Rêð

и формулировать

гипотезы приемки

è

браковки в

âèäå

P1

P0

неравенств Rô³Rêð è Rô<Rêð. Однако в

ýòîì

случае

a=P1(Rô=Rêð)=1-P0(Rô=Rêð)

è

b=P0(Rô=Rêð), т.е. a+b=1. Следова-

1-a

тельно, в этом случае никакими соче-

таниями значений n è Rïð

невозможно

обеспечить одновременно малые зна-

чения a и b. Поэтому такой "одно-

уровневый"

контроль

надежности

b

практически не применяется.

0

R1

R

Rô

Значение

R1 устанавливается

0

â

стандартах

èëè

технических

Рис.9.3. Риск заказчика и изготовителя.

условиях на

изделие,

величина

R0 определяется разработчиком и изготовителем и на нее должно быть

ориентировано производство изделия. Однако в экономически обоснован-

ных случаях допускается размещать интервал [R1,R0] относительно значе-

ния, заданного в стандартах или технических условиях Rïð таким образом,

чтобы обеспечить равенство ущерба потребителя от приемки ненадежных

изделий и изготовителя - от браковки надежных [4]. Если ущерб потреби-

теля сопоставим с ущербом изготовителя, то интервал [R1,R0] размещается

симметрично

относительно

установленного

значения

Rïð

(ïðè

ýòîì

P0»0,5). Если ущерб потребителя невелик по сравнению с ущербом изго-

товителя, то интервал [R1,R0] смещается влево вплоть до крайнего поло-

жения R0=Rïð. Если, наоборот, ущерб изготовителя невелик по сравнению

с ущербом потребителя, то интервал [R1,R0] смещается вправо вплоть до

крайнего положения R1=Rïð [5].

Риски a и b назначаются достаточно малыми (от 0,001 до 0,2) по дого-

воренности между изготовителем и заказчиком. Аналитическая форма

функций P0(Rô) è P1(Rô) определяется видом параметра надежности R è

законом его распределения в генеральной совокупности.

Критерий согласия Неймана-Пирсона является основой контрольных ис-

пытаний на надежность методом однократной выборки.

9.1.2 Одноступенчатый контроль вероятности отказа

Если контролируемым показателем надежности является вероятность отказа q(t0) или вероятность безотказной работы p(t0)=1-q(t0) за время t0, это значит, что в партии изделий объемом N имеется M дефектных изделий, время безотказной работы которых меньше t0, òàê ÷òî q(t0)=M/N.

В качестве контролируемых уровней надежности R0 è R1 используются нормальная q0(t0) и максимально допустимая q1(t0) вероятности отказа за время t0. Проверяемые гипотезы формулируются следующим образом:

H0:	qô(t0) £ q0(t0)	èëè M £ M0 =q0(t0)×N,	(9.6)
H1:	qô(t0) ³ q1(t0)	èëè M ³ M0 =q1(t0)×N,	(9.7)

170

Испытания выборки объемом n проводятся по плану [nUt0]. Подсчитывается количество отказавших изделий r, которое и является выборочной характеристикой R*. Тогда условие принятия гипотезы H0 (приемки) можно представить в виде r≤c, а условие принятия H1 (браковки) - в виде r>c, ãäå c (допустимое число отказов) является прие- мочно-браковочным нормативом

P

1

0

P		P1
0
1−α
α	β
q0	q1	qô

Рис.9.4. Оперативная характеристика контроля вероятности отказа

Rïð в условиях критерия Неймана-Пирсона. Время (или наработка) t0, за которое заданы проверяемые вероятности q0(t0) è q1(t0), определяет продолжительность испытаний, однако если до его истечения число отказов r превысит допустимое значение c, испытания прекращаются досрочно.

Вид оперативной характеристики для контроля по вероятности отказа показан на рис.9.4. По формулам (9.4) и (9.5) из рис.9.4 можно выразить риски изготовителя и заказчика:

1 - a = P0 (qô = q0 ) = P(r £ c / qô = q0 ),

(9.8)

b = P0 (qô = q1) = P(r £ c / qô = q1),

ãäå P0 - вероятность приемки гипотезы H0 (здесь и далее в обозначениях вероятностей время или наработка t опущены).

Сравнение выражения (9.8) с определением интегральной функции распределения случайной величины (см.гл.2) показывает, что вероятностью приемки партии является значение интегральной функции распределения дискретной случайной величины r (числа отказов в выборке объемом n) при значении аргумента r=c.

В самом общем случае распределение r является гипергеометрическим (см.гл.2), и вероятность приемки партии

c		Cr	× Cn−r
P0 (qô ) = P(r £ c) = å		M	N − M	.	(9.9)
			Cn
r =	0		N

Система уравнений (9.8) в случае гипергеометрического распределения аналитического решения относительно n è c не имеет.

Если объем выборки мал (n<0,1N), то распределение количества отказов r описывается биномиальным законом (см.гл.2) с параметром p=qô. В этом случае система (9.8) запишется в виде [5]

c		ü
b = å Cnr q1r (1 - q1)n−r ,		ï		b = Fá (ñ, n, qô = q1),			ü
r = 0		ï	èëè				ï	(9.10)
c		ý					ý
	−	ï		1 - a = F	(ñ, n, q = q		),ï
1 - a = å Cnr q0r (1 - q0 )n
		r ,ï		á	ô	0	þ
r = 0		þ

ãäå Fá(ñ,n,qô) - значение интегральной функции при аргументах ñ, n è qô.