84

Теперь рассчитаем момент инерции I0 стержня относительно оси, проходящей через центр инерции (середину) стержня. Относительно оси, прохо-

I		I0	дящей через конец стержня I								1	m 2 .		Расстояние
											3
	a	C	между осями a			1		(рис. 1.59). Тогда по теореме
						2
			Штейнера	1	m 2 I			m	1	2 . Отсюда			I			1	m 2 .
	Рис. 1.59
				3			0							0	12
								2

Видим, что в любом случае момент инерции тела представляется в виде I = kmr2, где r – какой-либо характерный размер тела, а k – коэффициент пропорциональности, зависящий от формы тела. Единица измерения момента инерции – кг∙м2.

1.8.5.Свободные оси вращения. Главные оси инерции

Рассмотрим твѐрдое тело, которое может вращаться вокруг неподвижной вертикальной оси. Чтобы удержать ось от перемещений в пространстве,

							заключим ее в подшипники. При вращении
							тела возникают силы взаимодействия между
		I3	O3	O
				2
							осью и подшипниками, удерживающие ось
O					O		вращения в заданном положении. В случае
1				1		I1
							вращения однородного симметричного тела
							вокруг оси симметрии силы бокового давле-
							ния подшипников на ось не возникают. В от-
	I2	O2	O3
							сутствие силы тяжести подшипники можно
		Рис. 1.60.					было бы убрать – ось и без них сохраняла бы
							своѐ положение в пространстве. Ось враще-

ния, положение которой в пространстве остается неизменным в отсутствие внешних сил, называется свободной осью тела.

Для тела любой формы и с произвольным распределением массы существуют три взаимно перпендикулярные, проходящие через центр инерции тела оси, которые могут служить свободными осями. Они называются главными осями инерции тела. Моменты инерции относительно главных осей называются главными моментами инерции тела.

Так, для прямоугольного параллелепипеда главные оси инерции O1O1 , O2O2 , O3O3 проходят так, как показано на рис. 1.60, а моменты инерции относительно этих осей в общем случае не равны.

Рис. 1.61.

						85
		O			У	тел с осевой симметрией одной главной
		1			осью инерции служит ось симметрии, а остальными
I1			I3
					– любые две взаимно перпендикулярные оси, прохо-
			O
					дящие	через центр	инерции, и перпендикулярные
I2			3
O			O	оси симметрии (рис.			1.61). Для этих осей в общем
2			2			I1 I2 I3 . Такое тело называется симмет-
					случае
O3					ричным волчком. Примером симметричного волчка
		O1			может	служить тело цилиндрической формы или
					юла.

У тела с центральной симметрией ни одна из главных осей не фиксирована, ими могут служить любые три взаимно перпендикулярные оси, проходящие через центр симмет-

рии. Для этих осей моменты инерции равны I1 I2 I3 . Такое тело называется шаровым волчком. Примером шарового волчка может служить тело в форме шара или в форме куба.

Если тело вращается в условиях, когда какое-либо воздействие извне отсутствует, то устойчивым оказывается только вращение вокруг главных осей, соответствующих максимальному и минимальному значениям момента инерции. Вращение вокруг оси, соответствующей промежуточному по величине моменту инерции, будет неустойчивым. Можно легко наблюдать это явление, бросая вращающийся прямоугольный брусок (спичечный коробок, коробку из-под конфет).

Под действием внешней силы устойчивым является вращение тела вокруг главной оси, соответствующей максимальному моменту инерции Imax .

1.8.6. Тензор инерции тела

y

y

d y

dm

r	dx
dz
z	x	x

Рис. 1.62.

Определим, в каком соотношении находятся моменты инерции тела, вычисленные относительно различных координатных осей. Для этого разобьем тело на совокупность материальных точек массой dm (рис.1.62). Затем дважды запишем одно и то же выражение равное r2dm , где r модуль радиус-

вектора материальной точки массой dm. Сложим и перегруппируем оба равенства:

86

r2dm (x2 y2 z2 )dm

r2dm (x2 y2 z2 )dm

2 r2dm (z2 y2 )dm (x2 z2 )dm (x2 y2 )dm

Как видно из рис. 1.62, z2 y2 dx2 , x2 z2 dy2 , x2 y2 dz2 это квадраты расстояний от материальной точки до осей координат x, y и z . Тогда

dx2dm Jxx момент инерции тела относительно оси х;

dy2dm J yy момент инерции тела относительно оси у;

dz2dm J zz момент инерции тела относительно оси z, и

2 r2dm Jxx J yy Jzz .

Для плоских тел, лежащих в плоскости xy, dz r , r2dm Jzz , тогда

Jzz Jxx J yy .

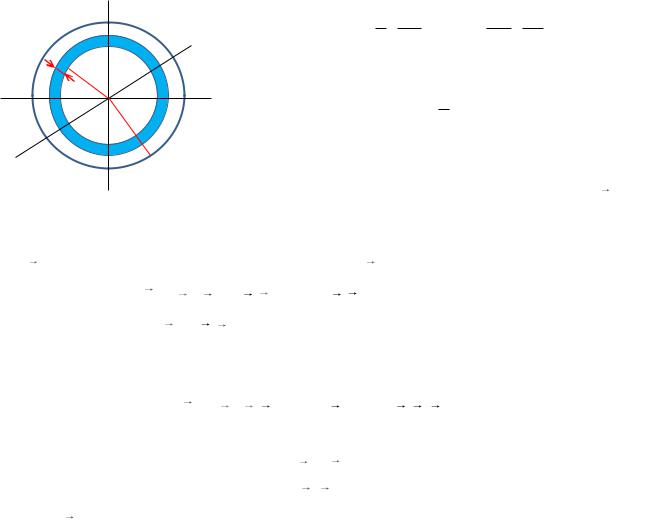
Для тела в форме шара, если ось вращения проходит через центр масс, то все три момента инерции равны: Jxx J yy Jzz . Найдем, например, J zz .

J zz 23 r2dm.

Разобьем шар на очень тонкие сферические слои (рис. 1.63) массой

dm dV , где плотность вещества шара.

m

m

3m

.

3 R

3

4 R

3

V

4

dV объем сферического слоя.

dV 4 r2dr.

Масса сферического слоя dm

3m

4 r2dr

3m

r2dr.

4 R3

R3

Подставляя в формулу для момента инерции, получим:

87

y

2

3m R

2m R5

J zz 3

R3

r4dr

R3 5 ,

0

dr

r

R

x

J zz

2 mR2.

5

z

Теперь

рассмотрим

тело

произвольной

Рис. 1.63.

формы, вращающееся с угловой скоростью

вокруг некоторой оси, проходящей через

центр масс. Совместим с центром масс начало координат. Момент импульса

тела L складывается из моментов импульсов dL материальных точек, состав-

ляющих это тело. dL r ,dp r ,v dm r ,v dm.

Учитывая, что v , r ,

и применяя свойство двойного векторного

произведения (см. Приложение), получим

dL r , ,r dm r2dm r (r , )dm.

Используя разложения векторов r и по осям координат, их скалярное

произведение можно представить как r , x x

y y z z . Тогда проекции

вектора dL на оси координат запишутся как

dL

(r2

x2 )dm

y

xydm

xzdm;

x

x

z

x yxdm y r2

y2 dm z yzdm;

dLy

x zxdm y zydm z r 2

z2 dm.

dLz

Как видно из рис. 1.62, r2 x2 d 2 , r

2 y2

d

2

,

r2

z2

d 2 это квад-

x

y

z

раты расстояний от материальной точки до осей x, y, z. Интегрирование по-

лученной системы уравнений, придем к выражениям для проекций вектора

момента импульса всего тела:

Lx

LyLz

x dx2dm y xydm z xzdm;

x yxdm y d y2dm z yzdm;

x zxdm y zydm z dz2dm.

88

Величины dx2dm Jxx , dy2 dm J yy , dz2dm Jzz есть моменты инерции тела относительно осей x, y, z, а величины

xydm J xy ; xzdm J xz ; yxdm J yx ;yzdm J yz ; zxdm J zx ; zydm J zy

называют центробежными моментами инерции.

Совокупность всех этих величин, записанную в виде матрицы, называют тензором инерции тела:

ˆ		J xx	J xy	J xz
J	J yx		J yy	J yz .
		J zx	J zy
				J zz

Компоненты Jxx , J yy , Jzz являются диагональными элементами тензора,

остальные недиагональными. Величины, расположенные симметрично относительно диагонали, попарно равны: Jxy J yx , Jxz Jzx , J yz Jzy . Такой тен-

зор называется симметричным.

Матрицу-столбец вектора L можно записать как произведение матрицы момента инерции на матрицу-столбец вектора :

L			J
	x				xx
Ly			J yx
L				J zx
	z

J xy J yy J zy

J

J

J

J xz

x

xx x

xy y

xz

z

J yz

y

J yx x J yy y J yz z

J zz

J

J

J

zz

z

zx x

zy y

z

или

ˆ

L J .

Момент импульса тела L весьма сложно зависит от распределения масс в теле. Его направление в общем случае не совпадает с направлением угловой скорости вращения .

Если оси координат x, y, z направить вдоль главных осей инерции тела, то центробежные моменты инерции будут равны нулю, и тензор инерции приводится к диагональному виду: