128

Длиной волны называют минимальное расстояние между двумя точками среды в направлении распространения волны, колеблющимся с разностью фаз равной 2 радиан.

Запишем фазы колебаний для двух точек среды с координатами x1 и x2 и определим разность этих фаз, вычитая одно уравнение из другого:

t

kx

1

1

2

t

kx

2

.

2

k(x x )

1

2

1

Если расстояние между точками x2 x1

равно длине волны , то раз-

ность фаз колебаний в этих точках равна 2 ,

т. е. 2 k . Тогда волновое

число

k

2

.

С другой стороны, k

, тогда

2

. Отсюда выразим длину волны:

v

v

2

v . Учитывая, что

2

T и T

1

, получим:

vT ;

v

;

v .

2.2.2. Волновое уравнение

Аналогично основному уравнению динамики, которое описывает все возможные движения материальной точки, для волновых процессов существует волновое уравнение, являющееся обобщенным выражением волн независимо от их конкретного вида. Это дифференциальное уравнение в частных производных, связывающее изменения функций, характеризующих волну, во времени и пространстве. Рассмотрим это на примере плоской волны, описываемой уравнением:

s Acos( t kx) .

(2.20)

129

Найдем первую и вторую частные производные колеблющейся величины s по времени t :

	s	A sin( t kx) ,
	t
	2s	A 2 cos( t kx) .		(2.21)
	t2
	Сравнивая (2.20) и (2.21), получим:
		2s	2s .	(2.22)
		t2

Теперь найдем первую и вторую частные производные колеблющейся величины s по координате x :

s	Ak sin( t kx),
x	,

2s Ak 2 cos( t kx).

x2

Сравнивая (2.20) и (2.23), запишем:

2s k 2s . (2.24)

x2

С учетом того, что k v , уравнение (2.24) принимает вид:

так как 2s 2s (см. уравнение (2.22)), тоt2

2s 1 2s .

x2 v2 t2

(2.23)

	2s	2s	1	, а,
	x2		v2

(2.25)

Это и есть одномерное волновое уравнение. Оно играет важную роль в теории волновых процессов. Если мы, исходя из законов механики, при изучении некоторого явления придем к уравнению (2.25), то сразу можно утверждать, что мы имеем дело с волновым процессом, скорость распространения v которого легко найти из сопоставления полученного уравнения с (2.25).

130

В общем случае характеристики волн зависят от трех пространственных координат, и волновое уравнение записывается в следующей форме:

2s

2s

2s

1 2s

.

x2

y2

z2

v2 t2

Применяя оператор Лапласа

2

2

2

, запишем это уравне-

x2

y2

z2

ние в более коротком виде:

s 1 2s .

v2 t2

			2.2.3. Энергия волны
Энергия одной колеблющейся частицы равна W								kA2		, где коэффици-
						1			2
ент жесткости k m 2		, m	масса одной частицы,			0	циклическая частота
1	0	1
собственных колебаний этой частицы. Тогда W1				m			2 A2		. Определим энер-
					1	0
						2

гию колеблющихся частиц среды в единице объема, так называемую плотность энергии волны w . Плотность энергии волны равна произведению энергии одной частицы на концентрацию этих частиц n (число частиц в единице

объема). То есть w nW1		nm 2 A2		, а, учитывая, что произведение nm1 равно
		1	0
			2

плотности среды , получим:

2 A2 w 0 .

2

Поток энергии это энергия, переносимая волной в единицу време-

ни dWdt . Поток энергии измеряется в ваттах [Ф]=1 Дж/c= 1 Вт.

Плотность потока энергии U это поток энергии, переносимый волной через единицу площади, перпендикулярной направлению распростране-

ния волны: U ddS . Если энергия переносится равномерно по всей площади,

				131
то U		. Плотность потока энергии измеряется в ваттах на квадратный
	S
метр:	U			1	Вт	.
					м2

Через площадку S в единицу времени передается энергия колеблющихся точек среды, удаленных от площадки на расстояние меньшее или равное скорости распространения волны v (рис. 2.19). Передаваемая энергия равна энергии волны в объеме прямоугольного паралелепипеда

площадью основания S и длиной ребра

S

wSv,

v

где w объемная плотность энергии волны,

Sv объем

Рис. 2.19.	паралелепипеда. Тогда плотность потока энергии будет рав-
	на U	wSv	. После сокращения на S	получим:
		S

U wv .

Направление скорости распространения волны совпадает с направлением передачи энергии, что позволяет записать последнее равенство в векторной форме:

U wv .

Таким образом, плотность потока энергии U это векторная величина, совпадающая по направлению со скоростью распространения волны.

Интенсивность волны I есть усредненное значение плотности потока энергии по времени I U или I wv . Так как плотность энергии волны прямо пропорциональна квадрату амплитуды колебаний, то и интенсивность волны прямо пропорциональна квадрату амплитуды колебаний I A2 .

2.2.4. Интерференция волн

Интерференцией волн называют явление наложения волн в пространстве, в результате которого происходит перераспределение энергии результирующей волны в пространстве. В некоторых точках среды амплитуда результирующих колебаний принимает максимальное значение, в других мини-

132

мальное. Наиболее устойчивая интерференционная картина наблюдается при наложении когерентных волн.

Волны называют когерентными, если для каждой точки волнового поля разность фаз дошедших колебаний не изменяется с течением времени, т. е. остается величиной постоянной. Из этого определения следует, что когерентными волнами могут лишь волны с одной и той же частотой.

Рассмотрим случай, когда одна волна s1 A1 cos( 1t k1r1) с частотой 1

проходит	до	точки наблюдения M			путь r1 а	другая волна
S	r1		s2 A2 cos( 2t k2r2 )		с частотой 2	проходит путь
1
		M	r2	(рис. 2.20). При наложении в точке M фазы со-
			ставляющих колебаний соответственно равны
	r2
					1 1t k1r1,
S2
					2 2t k2r2.
Рис. 2.20.				Тогда разность фаз накладываемых колеба-
ний 1 2	( 1	2 )t k2r2		k1r1 . Если накладываемые волны обладают раз-

ными частотами, эта разность фаз зависит от времени и не остаѐтся величиной постоянной, т. е. такие волны не будут когерентными. При наложении волн с одной и той же частотой 1 2 и волновым числом k2 k1 k разность фаз 1 2 k(r2 r1 ) . Теперь эта разность фаз не зависит от времени и остается величиной постоянной, т. е. такие волны будут когерентными. Величину r2 r1 называют разностью хода двух волн. Разность фаз накладываемых колебаний 1 2 связана с разностью хода соотношением

k или 2 .

2.2.4.1. Условие максимума и минимума

Максимум интенсивности результирующей волны возникает в тех точках, в которых разность фаз слагаемых колебаний равна четному числу (в этом случае говорят, что колебания приходят в одной фазе), т. е.

2m ,

						133
	где m			произвольное целое число (m = 0, 1, 2, …). С учетом того, что
		2		, запишем:	2	2m . Сократив на 2 и выразив разность хо-

да , получим условие интерференционного максимума:

max m 2m 2 .

При наложении когерентных волн колебания усиливают друг друга, когда в разности хода укладывается целое число длин волн или четное число полуволн.

Минимум интенсивности будет в тех точках, в которых складываемые

колебания отличаются по фазе на нечетное число								(колебания приходят в
противофазе).			Следовательно,				(2m 1) .	С учетом того, что
	2	, запишем:		2	(2m 1) или
						min	(2m 1) .
							2

Минимумы интенсивности результирующей волны находятся в тех точках среды, для которых в разности хода слагаемых волн укладывается нечетное число полуволн.

2.2.4.2. Стоячие волны

Частным случаем интерференции волн является образование стоячей волны. Стоячие волны возникают при наложении бегущей и отраженной волны от границы раздела двух сред. Например, на упругом натянутом шнуре, один конец которого закреплен, а другой приводится в колебательное движение. В этом случае происходит отражение от закрепленного конца шнура. Если конец шнура не будет закреплен, т. е. будет свободным, а другой конец шнура привести в колебательное движение, то и в этом случае будет наблюдаться стоячая волна, отраженная волна возникает при отражении от свободного конца шнура. Запишем уравнения бегущей и отраженной волн. Для этого поместим начало координат в точку, в которой волна испытывает отражение. Если бегущая волна распространяется против оси x , то ее уравнение будет иметь вид:

s1 Acos( t kx) .

134

Физические условия отражения волны от закрепленного конца шнура и свободного отличны, но амплитуда отраженной волны в обоих случаях равна амплитуде падающей, так как энергия волны не может передаваться далее. Если обозначить изменение фазы волны при отражении через , то уравнение отраженной волны записывается в виде:

s2 Acos( t kx ) .

Оно описывает волну, распространяющуюся в направлении оси x , поэтому знак у kx изменился на противоположный.

Сложение падающей и отраженной волн приводит к следующему результату:

	s s1 s2		A[cos( t kx) cos( t kx )].
Применив к этому уравнению тригонометрическое тождество
	cos cos 2cos cos						,
					2	2
получим уравнение стоячей волны:
		s					(2.26)
			2Acos kx	cos t		.
				2		2
Множитель			не зависит от времени и дает амплитуду стоячей
	2Acos kx
		2

волны:
Aст	2A
			cos kx		,
				2

являющуюся периодической функцией координаты x .

Точки, в которых амплитуда стоячей волны Aст 0 , называются узлами стоячей волны, а точки, в которых амплитуда стоячей волны максимальна ( Aст 2A ), называются пучностями стоячей волны.

При отражении волн от более плотной среды (с большим волновым со-

противлением) в точке отражения (х = 0) получается узел, т. е.	cos		0 и
		2
. Таким образом, фаза колебаний скачком изменяется на	радиан, а

135

уравнение стоячей волны после подстановки в (2.26) и применения тригонометрических формул приведения имеет вид:

s 2Asin kxsin t .

При отражении от менее плотной среды на границе раздела сред полу-

чается пучность, т. е. cos 2 1 и 0. Таким образом, при отражении от

среды с меньшим волновым сопротивлением фаза колебаний не изменяется, а уравнение стоячей волны принимает вид:

s 2Acos kxcos t .

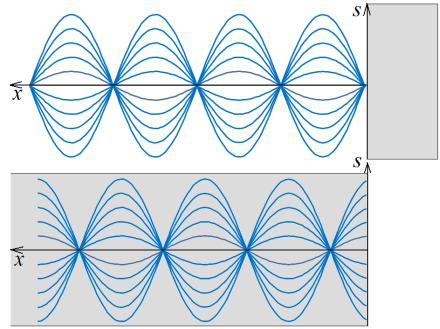
Графики стоячих волн при отражении от более плотной и менее плотной среды приведены на рис. 2.21. Более плотная среда закрашена. Как видим из рисунка, расстояние между узлами или между пучностями равно половине

Рис. 2.21.

волны 2 , а между узлом и пучностью четверти волны 4 . Там, где был узел

при отражении от более плотной среды, стала пучность при отражении от менее плотной среды и наоборот. Все точки среды между двумя соседними узлами будут колебаться в одной фазе, но с разными амплитудами. При перехо-