109
3)			При разности фаз				sin 1, cos 0 и уравнение (2.6) перехо-
					2
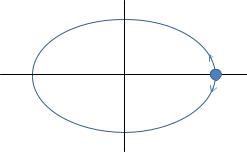
дит			в		уравнение эллипса симметричного относительно осей координат:
2					2
	x			y		1. Исследуем направление движение тела по этому эллипсу. Поло-
	2				2
	A			B

жение тела в момент времени t 0 находим из уравнений (2.2) и (2.3). Если

2 , то

x Acos t
		t		Asin t	(2.7)
y Acos
			2

Если 2 , то

x Acos t
					(2.8)
		t		Asin t
y Acos
			2

y

B
		2
	A
		2

	В момент времени t 0 в обоих случаях ко-
	леблющееся	тело имеет координаты
x	x A, y 0.	При разности фаз в по-
		2

следующий момент времени координата y становится отрицательной. Движение совершается по часовой стрелке (рис. 2.9). При

		разности фаз			в последующий мо-
	Рис. 2.9.			2

мент времени координата y становится положительной. Следовательно, движение совершается против часовой стрелки.

2.1.4. Скорость и ускорение при гармонических колебаниях

Рассмотрим материальную точку, совершающую гармоническое колебание по закону

x Acos( t ) .

(2.9)

110

Определим закон, по которому изменяются скорость и ускорение этой точки. Взяв производную колеблющейся величины x по времени t , найдем скорость движения точки в проекции на ось х:

vx dxdt A sin( t ) .

Применив тригонометрическую формулу приведения, запишем

vx		t
	A cos			,
			2

где A амплитуда скорости колеблющейся точки. Сравнивая (2.9) и

видим, что скорость опережает колеблющуюся величину по фазе на

2

ан.

(2.10)

(2.11)

(2.11),

ради-

Найдем уравнение изменения ускорения как первую производную скорости по времени (или как вторую производную от колеблющейся величины x по времени t ). В проекции на ось х

	a			dvx				d 2 x	A 2 cos( t )	(2.12)
		x
				dt				dt2
									или
				a	x	A 2 cos( t ) ,				(2.13)
где A 2	амплитуда ускорения. Сравнивая (2.9) и (2.13), приходим к выводу,
что ускорение опережает колеблющуюся величину по фазе на радиан.

2.1.5. Дифференциальное уравнение свободных гармонических колебаний

Определим силу, действующую на тело, совершающее свободные гармонические колебания. Для этого применим второй закон Ньютона Fx max .

Сравнивая (2.9) и (2.12), запишем

a	x	2 x ,	(2.14)

тогда сила будет равна:	F m 2 x .
	x

111

То есть сила, действующая на тело, прямо пропорциональна его смещению x от положения равновесия. По такому же закону изменяется упругая сила при растяжении и сжатии пружины на величину x : Fx kx . Для пружины k называют коэффициентом упругости. Для тела, совершающего гармонические колебания, величину k m 2 называют коэффициентом квази-

упругой силы или коэффициентом жесткости, а силу, действующую на тело,

записывают в виде

Fx kx .

Запишем в уравнении (2.14) ускорение как вторую производную колеб-

	лющейся величины x по времени t :	d 2 x	2 x или	d 2 x	2 x 0 . Для соб-
		dt2		dt2

ственных колебаний циклическую частоту обозначают с индексом нуль, тогда

d 2 x 2 x 0 . dt2 0

Это уравнение называют дифференциальным уравнением свободных гармонических колебаний. Его также можно записать в следующем виде:

x 02 x 0 .

2.1.6.Маятники

2.1.6.1.Пружинный маятник

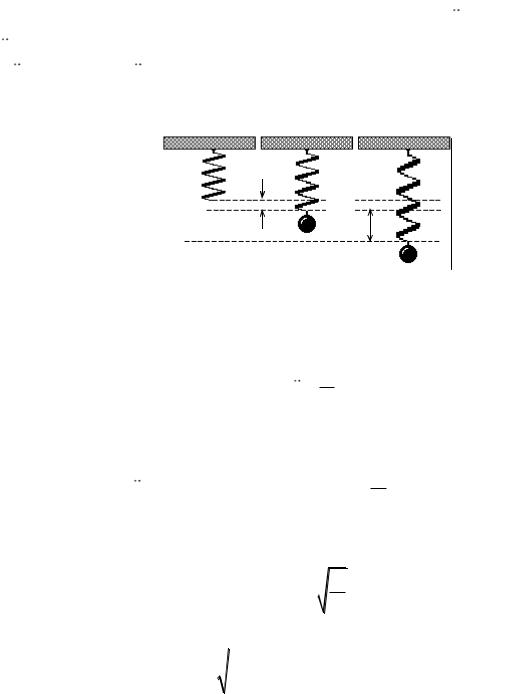
Пусть на пружине жесткостью k подвешено тело массой m (рис. 2.10). Массу пружины предполагаем настолько малой, чтобы при колебаниях ею можно было пренебречь. Такая система называется пружинным маятником. Поместим начало отсчета оси x в точку, соответствующую равновесному положению тела в состоянии покоя. В этом положении благодаря действию силы тяжести пружина растянута на величину x0 , определяемую соотношением

mg kx0 .

(2.15)

112

При смещении тела на величину x из положения равновесия проекция силы, действующей на тело со стороны пружины, равна Fx k(x x0 ) . Тогда второй закон Ньютона в проекции на ось х имеет вид mx mg k(x x0 ) , где

x ускорение тела. С учетом (2.15) это уравнение можно переписать в виде mx kx , или mx kx 0. Разделив обе части уравнения на массу m , получим

		0
х0	х

х

Рис. 2.10.

x mk x 0 .

Сравнивая это уравнение с дифференциальным уравнением гармониче-

ских колебаний x 02 x 0 , найдем, что 02 mk . Циклическая частота собст-

венных колебаний пружинного маятника

0 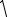mk ,

а период колебаний T 2		m		.
0		k

2.1.6.2. Физический и математический маятники

Уравнение движения колебательной системы можно получить не только из уравнений динамики, но и из закона сохранения энергии. Рассмотрим это на примере физического маятника.

113

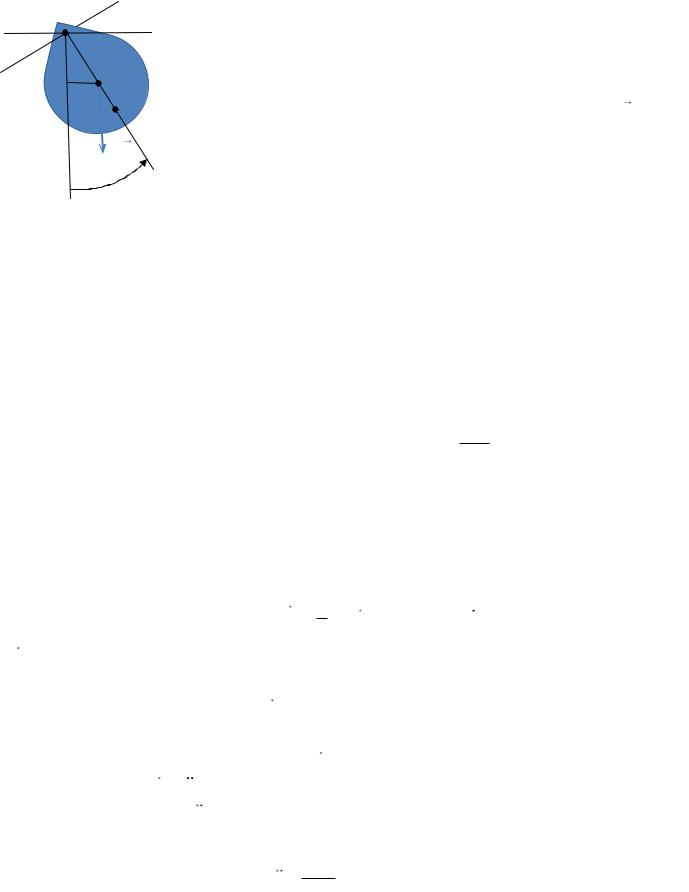
О	WП	0	Под физическим маятником понимают твердое те-
			ло, совершающее под действием силы тяжести колебания
h	a		вокруг неподвижной горизонтальной оси, не проходящей
A	С		через его центр масс. Обозначим буквой C центр масс
	О		твердого тела, к которому приложена сила тяжести	mg
	mg		(рис. 2.11).
			Отклонив маятник от положения равновесия,	мы
			сообщаем ему потенциальную энергию. Выберем за ну-
			левой уровень потенциальной энергии уровень горизон-
Рис. 2.11.			тальной оси колебаний. Тогда потенциальная энергия
			маятника будет равна Wп mgh , где h – глубина по-

гружения центра масс C маятника под нулевой уровень. Глубину погружения h определим из прямоугольного треугольника OAC : h a cos , где a – расстояние от центра масс C до оси колебаний O , – угол отклонения маятника от положения равновесия. Тогда Wп mga cos .

В процессе колебаний потенциальная энергия маятника Wп переходит в кинетическую энергию вращательного движения Wk I 2 2 , где I – момент

инерции маятника относительно оси колебаний, – угловая скорость поворота вокруг этой оси. Если не учитывать силы трения и силы сопротивления, то полная механическая энергия маятника остается величиной постоянной,

		I 2
W W W			mga cos const., а производная полной механической
k	п	2

энергии по времени равна нулю W 2I 2 (mga sin ) 0 . Учитывая, что, после сокращений получим

I mgasin 0 .

Производная угловой скорости равна второй производной угла поворота по времени . Для малых углов поворота , выраженных в радианах, sin . Тогда I mga 0 , и, после деления на момент инерции I , получим:

mga 0 .

I

114

Сравнивая это уравнение с дифференциальным уравнением гармонических колебаний x 02 x 0 , видим, что при малых углах отклонения колеба-

ния будут гармоническими, а	2			mga				. Циклическая частота собственных
	0
					I
колебаний физического маятника
							mga		,
			0					I
а период этих колебаний T0 2			I		.
		mga

Математическим маятником называют систему, состоящую из невесомой и нерастяжимой нити, на которой подвешено тело, которое можно считать материальной точкой. Хорошим приближением к математическому маятнику служит небольшой тяжелый шарик, подвешенный на длинной тонкой нити. Обозначим длину нити подвеса через . Математический маятник – это частный случай физического маятника, момент инерции которого равен моменту инерции материальной точки I m 2 , – длина нити.

При малых углах отклонения от положения равновесия математический

маятник совершает гармонические колебания, период которых	T0	2	m	2	.
			mg

Сократив на m и , получим период колебаний математического маятника

T0 2 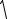g .

Приведенной длиной физического маятника называют длину такого математического маятника, период колебаний которого совпадает с периодом

физического маятника 2	пр	2		I			. Отсюда приведенная длина физи-
	g			mga
ческого маятника
					I			.
			пр
					ma