120

2.1.8.3. Добротность. Энергия затухающих колебаний

Для характеристики колебательной системы часто используется также

	величина Q		N , называемая добротностью колебательной системы и

пропорциональная числу колебаний N , совершенных за время релаксации. Энергия колеблющейся системы пропорциональна квадрату амплитуды

колебаний:

W

kA2

.

Учитывая,

что

A A e t ,

получим

2

0

W

k

A0e t 2

W0e 2 t , где W0

kA02

энергия колебательной системы в на-

2

2

чальный момент времени. Как видим, энергия затухающих колебаний изменяется по экспоненциальному закону, а скорость ее изменения со временем

равна

dW

2 W e 2 t 2 W , т. е. энергия убывает со скоростью равной

dt

0

2βW.

Найдем убыль энергии

за

время,

равное

периоду колебаний:

W

dW

T 2 WT . Если

учесть, что

T ,

то W 2W , тогда

dt

W , а добротность колебательной системы

2W

W

Q

2

.

W

Добротность колебательной системы с точностью до множителя 2 равна отношению энергии, запасенной в системе в данный момент, к убыли этой энергии за период колебаний.

При достаточно большом затухании ( 0 ) система совершает апериодическое движение: выведенная из положения равновесия, она возвращается в это положение, не совершая колебаний.

2.1.9. Вынужденные колебания. Резонанс

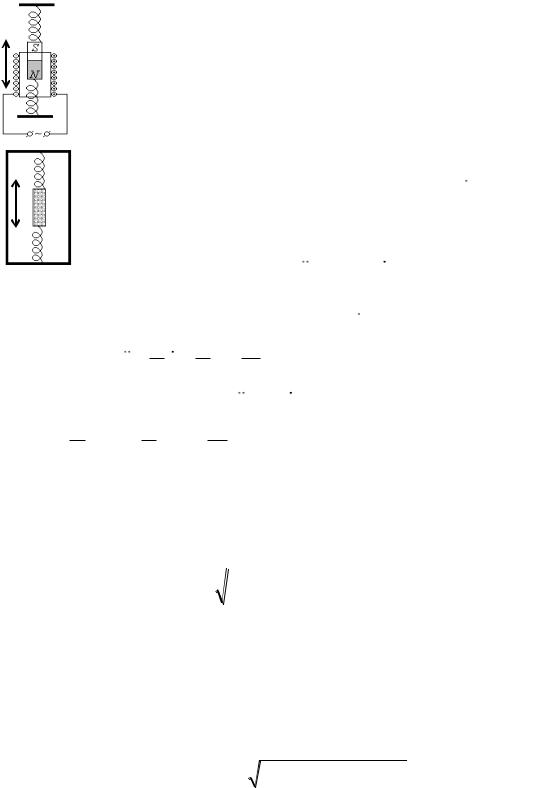
Рассмотрим колебательную систему, совершающую движение под действием внешней вынуждающей силы, изменяющейся по гармоническому закону. Установкой для наблюдения вынужденных колебаний может служить постоянный магнит, подвешенный внутри катушки на двух вертикально рас-

121

положенных пружинах (рис. 2.15 а). При прохождении переменного тока через катушку возникает переменное магнитное поле, действующее на постоян- а ный магнит с силой, изменяющейся по гармоническому закону.

Переменную силу можно создать и другим способом, если пружинный маятник закрепить в рамке, колеблющейся в вертикальном направлении (рис. 2.15 б). Тогда в системе отсчета, связанной с рамкой, на маятник будет действовать переменная сила инерции. Кроме внешней вынуждающей силы F0 cos t , изме-

б	няющейся с частотой , на маятник действуют квазиупругая си-
	ла Fупр kx и сила сопротивления Fсопр rx . Запишем уравне-
	ние динамики (второй закон Ньютона) для этого тела:
	mx kx rx F0 cos t .
Рис. 2.15.	Перенесем слагаемые kx и rx в левую часть и, после деления

на m , получим x mr x mk x Fm0 cos t или

x 2 x 02 x f0 cos t,

где 2 mr , 02 mk , f0 Fm0 . Полученное уравнение есть дифференциальное

уравнение вынужденных колебаний, решение которого при установившихся колебаниях записывается в виде:

	x		f0			cos t 0	.
		02 2		2 4 2 2

Установившиеся вынужденные колебания представляют собой гармонические колебания с частотой равной частоте вынуждающей силы . Амплитуда вынужденных колебаний

A			f0			(2.19)
	( 2		2 )2	4 2 2
0

зависит и от амплитуды вынуждающей силы F0 = f0m, и от частоты ее воздействия .

m 02

F0

		122
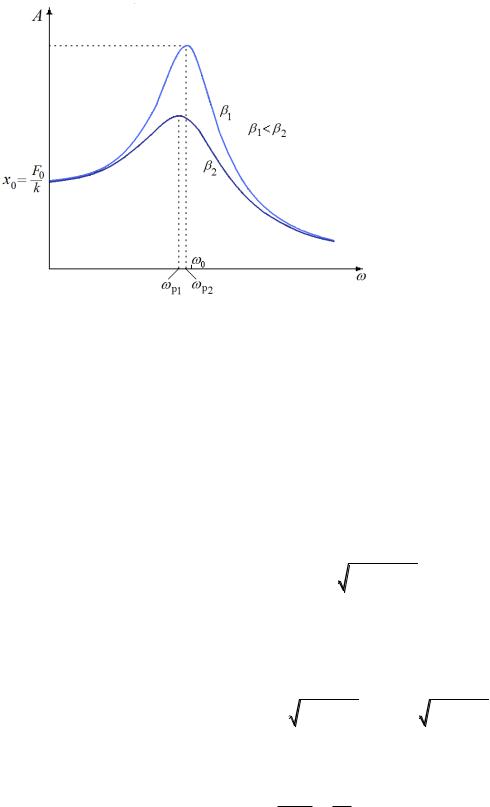
		Изменение частоты внеш-
		него воздействия приводит к из-
		менению амплитуды вынужден-
		ных колебаний. На рисунке 2.16
		показаны два графика зависимо-
		сти A(ω) при разных коэффици-
		ентах затухания 1	и 2 . При
		некоторой частоте	внешнего
		воздействия ω = ωр	амплитуда
		вынужденных колебаний при-
		нимает максимальное значение.
		Это явление называется резо-
	Рис. 2.16.	нансом. Определим резонансную
		частоту. Амплитуда	колебаний

максимальна, когда минимально подкоренное выражение 02 2 2 4 2 2

в знаменателе формулы для амплитуды (2.19). Взяв производную по и при-

равняв	ее к нулю, найдем резонансную частоту. Производная равна
4 02	2 8 2 , тогда
	4 02 р2 р 8 2 р 0
					и
		р		2 2 2 .
				0

Подставляя резонансную частоту в формулу для амплитуды, определим резонансную амплитуду:

Aр			f0				F0					.
		2 2					2m
				2					2	2
		0					0

Если частота внешнего воздействия 0, все кривые приходят к од-

ному и тому же значению x0 Fk0 , равному смещению системы из по-

ложения равновесия под действием постоянной силы, равной амплитудному значению вынуждающей силы F0 . Если частота , амплитуда вынужденных колебаний стремится к нулю A 0 .

123

При малом коэффициенте затухания, когда

0 , резонансная ампли-

туда

Aр

F0

F0

F0

.

2m 2

2

2m 0

1

2

2m 0

0

2

0

Умножим числитель и знаменатель на

, тогда

A

F0 0

. Учиты-

2m 2

0

р

0

вая, что

F0

x , получим

A

0

x

. Выразим циклическую частоту

че-

m 2

0

р

2

0

0

0

рез период колебаний:

2

,

тогда

A

x . Так как T есть лога-

T

0

T

р

0

рифмический декремент затухания,

следовательно, A

x , и отношение

р

0

Aр

Q определяет добротность колебательной системы. То есть доброт-

x

0

ность можно определить по графику зависимости амплитуды А вынужденных колебаний от частоты изменения вынуждающей силы (рис. 2.16) как:

Q Aр . x0

Колебания в системе отстают по фазе от воздействия вынуждающей силы на величину

			arctg	2		.
		0		2	2
				0

Отставание фазы вынужденных колебаний 0 от фазы вынуждающей силы различно в зависимости от частоты внешнего воздействия. Построим график зависимости 0 от от-

носительной частоты 0 (рис. 2.17). Для этого

выразим 0 в единицах :0

Рис. 2.17.