16

мя, называемое периодом вращения Т. Если в единицу времени (1 с) совершается ν оборотов, то период Т = 1/ν. Иначе число оборотов в единицу времени ν называют частотой вращения. Угловая скорость при равномерном вращении

t . Угловой путь за один оборот равен 2 радиан, тогда

2 2 .

T

1.1.4.Равномерное движение

Взависимости от того, как изменяются со временем скорость и ускорение материальной точки, ее движение может быть разделено на несколько видов. Простейшим является случай движения с постоянной по модулю ско-

ростью – равномерное движение.

Рассмотрим равномерное движение материальной точки с постоянной по модулю скоростью v const. по произвольной траектории. Из определения

	модуля скорости v	ds	следует, что элементарный путь ds, который матери-
		dt

альная точка проходит за время dt, находится как:

ds vdt .

Интегрируя, получим закон зависимости пройденного пути от времени наблюдения t:

s ds vdt s vt C.

Константу интегрирования C определим из начальных условий. Если в начале наблюдения при t = 0 путь материальной точки s s0 , тогда C s0 , а закон зависимости пути от времени наблюдения принимает вид:

s s0 vt.

Если в момент времени t = 0 пройденный путь s0 0 , тогда

s vt .

17

Равномерное движение не означает движения без ускорения, поскольку при криволинейном равномерном движении материальная точка обладает нормальным ускорением an . Равна нулю только тангенциальная компонента ускорения, поскольку скорость не меняется по величине. Для равномерного движения

a a

dv

.

n

dt

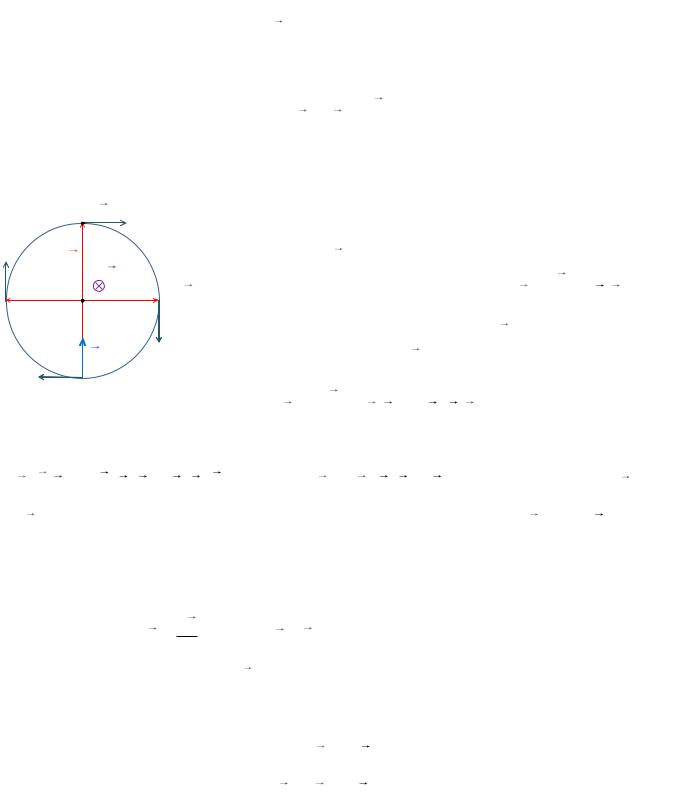
Рассмотрим равномерное

движение материальной точки по

v

окружности (рис. 1.10). Расположим начало координат в

центре этой окружности. В случае равномерного движе-

r

ния радиус-вектор r

прецессирует с угловой скоростью

и,

v

dr

, r .

согласно

уравнению прецессии,

dt

Вектор скорости материальной точки v также прецес-

an

сирует с угловой скоростью . Тогда вектор нормально-

го ускорения a

dv

,v , r . Применяя свой-

Рис. 1.10.

n

dt

ство

двойного

векторного

произведения

a b,c

b a c c a b , получим an r r 2. Так как векторы r

и взаимно перпендикулярны, первое слагаемое равно нулю, и an 2r . Пусть материальная точка движется равномерно по прямолинейной

траектории. Тогда вектор мгновенной скорости остается постоянным не только по модулю, но и по направлению. Согласно определению вектора мгно-

венной скорости v drdt . Тогда dr vdt . Интегрируя это выражение, найдѐм

зависимость радиус-вектора r движущейся материальной точки от времени наблюдения:

r dr

r vdt vt C.

Константу интегрирования C определим из начальных условий: если в начале наблюдения при t = 0 положение материальной точки определялось

18

радиус-вектором r0 (рис. 1.11), то C r0 , а зависимость радиус-вектора от времени принимает вид:

y		r r0 vt .
	vt	x x0 vxt
		В проекциях на оси координат	y y		v t.
r0
				0	y

	r	Ось x обычно проводят по траектории пря-
		молинейного движения, тогда пройденный мате-
		риальной точкой путь
		x

Рис. 1.11.	s x x0	vt.

1.1.5.Движение с постоянной тангенциальной составляющей

вектора ускорения aτ.

Определим зависимость модуля скорости от времени наблюдения, ис-

пользуя определение тангенциальной составляющей ускорения a ddtv . За

промежуток времени dt изменение модуля скорости dv a dt . Интегрируя, получим:

vdv

va dt a t C.

Константу интегрирования C определим из начальных условий: если в момент начала наблюдения при t = 0 материальная точка обладала скоростью, по модулю равной v0 , тогда C = v0 , а зависимость модуля скорости от времени наблюдения:

v v0 a t .

(1.2)

График этой зависимости показан на рисунке 1.12.

Аналогично определим зависимость пройденного пути от времени на-

блюдения. Из определения модуля скорости v dsdt выразим элементарный путь ds vdt . Интегрируя, получим:

				19
	v						s ds
	v	B				s vdt (v0 a t)dt
		A	a t				s v0t	a t	2	C.
	v
			C					2
	0
			D	Константу интегрирования определим из на-
	O	t	t
				чальных условий: если в момент времени t = 0 путь
		Рис. 1.12.		s = 0, тогда C = 0, а зависимость пути от времени
				принимает вид:
				s v0t	a t2
							.			(1.3)
						2

К такому же результату можно прийти, используя график зависимости скорости от времени v v0 a t . Путь, пройденный материальной точкой за время t, соответствует площади под графиком скорости. На рис. 1.12 эта площадь выделена цветом. Видно, что она равна сумме площадей прямоугольника OACD и треугольника АВС. Площадь прямоугольника соответствует v0t ,

		a t 2	. Таким образом, s v0t	a t2
	площадь треугольника				.
		2		2

Всю заштрихованную площадь можно также представить как площадь трапеции OABD, равную произведению полусуммы оснований v и v0 на вы-

соту t, тогда
	s v v0 .					(1.4)
				2
Из (1.2) выразим время,	t v v0			, и подставим его в (1.4), тогда
		a
	v v		v v			v2 v2
s	0			0	и s	0 .
	2		a			2a
1.1.6.	Равноускоренное движение

Движение называют равноускоренным, если оно происходит с постоянным вектором полного ускорения a const. Если тангенциальная составляю-

20

щая ускорения при этом не остаѐтся постоянной, то формулы для скорости и пути, полученные в предыдущем параграфе, не будут справедливы.

Примером такого движения может служить движение тела в однородном поле тяготения Земли или движение заряженной частицы в однородном электрическом поле плоского конденсатора.

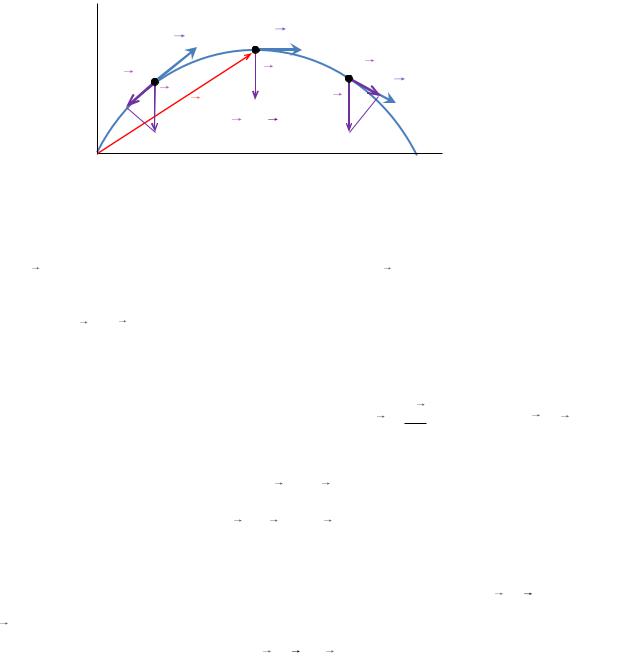
На рисунке 1.13 показана траектория движения камня, брошенного под углом к горизонту в поле тяготения Земли. Выберем оси координат таким образом, чтобы вектор скорости при движении тела лежал в плоскости xy.

y

		v	B	v
					C a v
a	A			a
	a		r		a
			a g

x

Рис. 1.13.

Во всех точках траектории камень обладает постоянным полным ускорением a , равным ускорению свободного падения g , а нормальная и тангенциальная составляющие полного ускорения не остаются постоянными. В точке А векторы a и v направлены противоположно и a 0 . В точке В a 0 ,

в точке С a 0 .

Определим зависимость вектора скорости от времени наблюдения. Ис-

ходя из определения вектора полного ускорения a ddtv , запишем dv adt .

Интегрируя, получим:

vdv

va dt at C.

Константу интегрирования С определим из начальных условий: пусть в начале наблюдения при t = 0 материальная точка имела скорость v = v0 , тогда C = v0 , а зависимость вектора скорости от времени принимает вид:

v = v0 at.

Проецируя каждый вектор на оси координат, получим

21

vx v0 x axtvy v0 y ayt ,

тогда модуль скорости v vx2 v2y .

Аналогично определим зависимость радиус-вектора r материальной точки от времени наблюдения. Из определения вектора скорости v = drdt за-

пишем dr vdt . Интегрируя, получим:

r dr

r vdt v0 at dt

r v0t at2 C. 2

Константу интегрирования определим из начальных условий: пусть в начальный момент отсчета времени t = 0 материальная точка имела радиусвектор r r0 , тогдa C r0 , а зависимость радиус-вектора от времени принимает вид:

r r	+ v t	at2	.	(1.5)
0	0	2

Если в момент времени t = 0 радиус-вектор r0 0 (точка начинает дви-

жение из начала координат), тогда r v0t at2 . 2

Для определения положения материальной точки в любой момент времени спроецируем каждый вектор, входящий в уравнение (1.5), на оси координат:

				axt2
x x0		v0 xt
				2
							,	(1.6)
					a t2
y y		v	t
					y
	0	0 y
				2
где координата x rx есть проекция радиус-вектора на ось Ох,								координата

y ry – проекция радиус-вектора на ось Оу.