40

где – коэффициент трения скольжения, зависящий от природы и состояния соприкасающихся поверхностей (в частности, от их шероховатости); Fn – модуль силы нормального давления, прижимающей трущиеся поверхности друг к другу. Согласно третьему закону Ньютона по величине эта сила равна силе реакции опоры N, тогда сила трения скольжения Fтр N . Сила Fтр направ-

лена в сторону, противоположную направлению движения данного тела относительно другого по касательной к трущимся поверхностям.

Сила сопротивления среды действует на тело при его движении в газе или жидкости. Эта сила зависит от вектора скорости тела v относительно среды и направлена противоположно ему: F kv , где k – положительный коэффициент, характерный для данного тела и данной среды. Этот коэффициент зависит, вообще говоря, от скорости v, однако при малых скоростях во многих случаях его можно считать постоянным.

1.5.4. Кинетическая энергия

Энергию, которой обладают движущиеся тела, называют кинетической энергией Wк.

Пусть частица массы m движется под действием некоторой силы F (в общем случае сила F может быть результирующей всех сил – как консервативных, так и неконсервативных). Найдем элементарную работу, которую совершает эта сила на элементарном перемещении dr . Имея в виду, что

F m ddtv и ds vdt , запишем величину элементарной работы как

A F ds

A mvdv d mv2 .2

Отсюда видно, что работа результирующей силы F идет на приращение некоторой величины (стоящей в скобках), которую и называют кинетической энергией:

Wmv2 .

к2

Изменение кинетической энергии материальной точки при перемещении из положения 1 в положение 2 равно алгебраической сумме работ всех

41

сил (как консервативных, так и неконсервативных), действующих на этом участке:

Wк 2 Wк1 A12 .

1.5.5.Потенциальная энергия

То обстоятельство, что работа консервативных сил зависит только от начального и конечного положений материальной точки в силовом поле, дает возможность ввести понятие потенциальной энергии. Потенциальная энергия является функцией координат точек силового поля. Силы поля, перемещая материальную точку, совершают работу равную уменьшению потенциальной энергии. В этом случае работа сил поля не зависит от вида траектории движения тела: A dWп или dWп A , следовательно,

dWп F dr.

(1.7)

При конечном перемещении из положения 1 в положение 2:

Wп 2 Wп1 A12 .

Потенциальная энергия материальной точки в силовом поле зависит от вида силового поля. Чтобы записать формулу потенциальной энергии материальной точки в каком-либо силовом поле, необходимо проинтегрировать выражение (1.7):

Wп F dr.

Неопределенный интеграл находится с точностью до постоянной интегрирования С. Эта постоянная определяется выбором точки силового поля, в которой потенциальная энергия условно принимается равной нулю.

1.5.5.1.Потенциальная энергия тела в гравитационном поле Земли

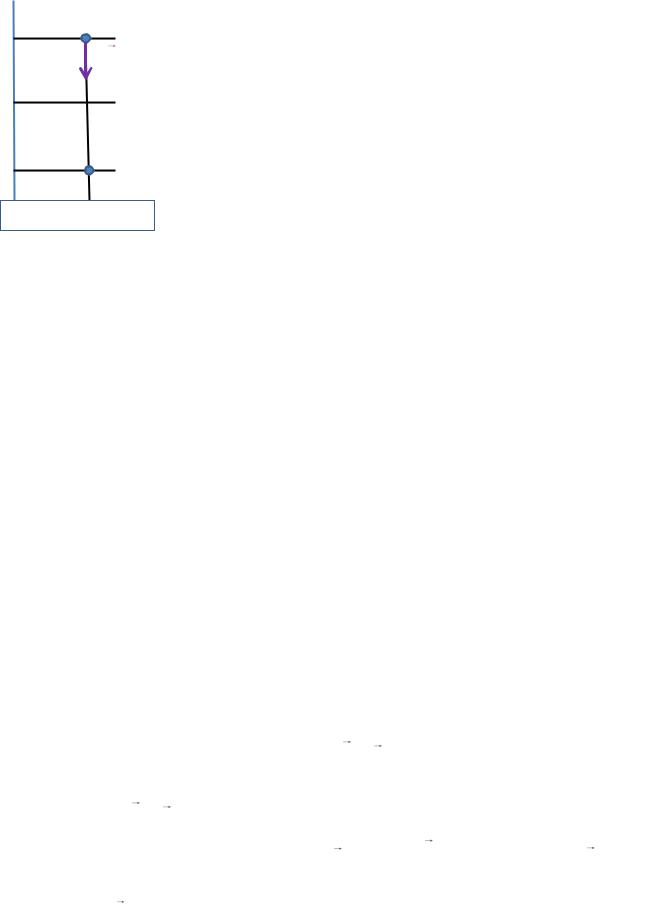
Рассмотрим потенциальную энергию тела, поднятого над поверхностью Земли на относительно небольшую высоту h << R, где R – радиус Земли. Тогда гравитационное поле Земли можно считать однородным. Сила тяжести mg , перемещая тело из 1-го состояния во 2-е, совершает работу А, равную произведению модулей силы и перемещения. Перемещение равно разности

y1	1	mg	h
y0			0
y2	2		-h

Рис. 1.26.

42

координат у1 и у2 (см. рис. 1.26). В свою очередь эта работа равна уменьшению потенциальной энергии:

А Wп1 Wп2 mg( y1 y2 ) .

Раскрыв скобки, запишем:

Wп1 Wп2 mgy1 mgy2 .

Из этого равенства следует, что зависимость потенциальной энергии от координаты y имеет вид:

Wп mgy C .

Значение постоянной С не влияет на разность значений потенциальной функции Wп в 1-ом и 2-ом состояниях. Оно определяется выбором точки, в которой потенциальная энергия условно принимается равной нулю, допустим в точке с координатой y y0 . Тогда 0 mgy0 C и C mgy0 . Потенциальная энергия тела в однородном гравитационном поле Земли

Wп mgy mgy0 mg( y y0 ) .

Для тела, находящегося выше уровня y0 , потенциальная энергия положительна: Wп mgh , где h y y0 – высота подъема тела над уровнем y0 . Для тела, находящегося ниже уровня y0 , потенциальная энергия отрицательна:Wп mgh , где h y y0 , h – глубина опускания тела под уровень y0 .

Теперь примем во внимание неоднородность гравитационного поля Земли. По определению потенциальной энергии

Wп F dr .

	Учитывая, что F dr Fr (r)dr , получим Wп Fr (r)dr .
	Для гравитационного поля Земли: F G			Mm		r	. Проекция силы F	на
				r2 r
	радиус-вектор r : F (r) G	Mm	, тогда
	r	r2

			43
		Mm		dr	Mm
Wп G		r2 dr GMm r2 G			r	C.
В бесконечно удаленной точке ( r ) значение потенциальной энергии
примем равным нулю. Исходя из этого, определим постоянную интегрирова-
ния С: 0 GMm C , т. е. С = 0. Тогда потенциальная энергия тела в гравита-
ционном поле Земли всегда отрицательна:
		W G Mm .						(1.8)
		п	r
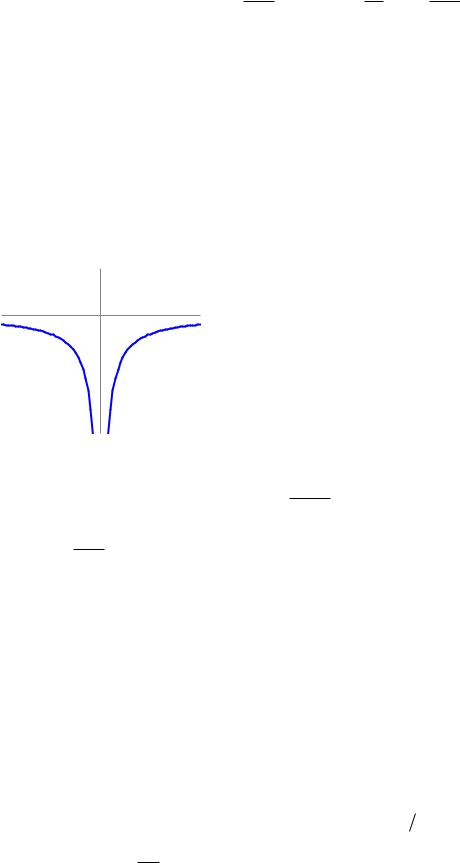
WП	Значение потенциальной энергии с ростом рас-
r	стояния r		увеличивается (рис. 1.27).
0		Покажем, что формула (1.8) не противоре-
	чит выражению для потенциальной энергии тела
	в	однородном		гравитационном			поле	Земли:
	Wп mgh . Найдем по формуле (1.8) потенциаль-
	ную энергию тела, поднятого над поверхностью
Рис. 1.27.	Земли на относительно небольшую высоту h<<R):

W G Mm , на поверхности Земли

п	R h

Wп0 G MmR . Тогда

Wп Wп0

G

Mm

G

Mm

G

Mm

G

Mm

R h

R

R

R h

или

1

1

h

Wп Wп0

GMm

GMm

.

R

R

h

R(R h)

Вынесем в знаменателе R за скобки и получим:

W W	mG	M		h	.
		R2
п п0				(1 h R)

Учитывая, что G RM2 g – ускорение свободного падения и h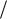 R 0 , запишем

44

Wп Wп0 mgh .

1.5.5.2.Потенциальная энергия упругих сил

Пусть закрепленная одним концом упругая пружина расположена вдоль оси х. Выберем начало координат так, чтобы в недеформированном состоянии координата свободного конца пружины была равна нулю. При растяжении или сжатии пружины эта координата принимает значение х. По определению потенциальной энергии Wп F dr Fxdx . Согласно закону Гука

Fx kx , и

kx2

Wп kxdx 2 C .

Примем, что в недеформированном состоянии (x = 0) пружина имеет потенциальную энергию равную нулю, тогда постоянная интегрирования C также равна нулю

( 0 k 0 C, C 0 ). Потенциальная энергия упругих сил определится выра-

2

жением:

Wп kx22 .

Графиком зависимости потенциальной энергии пружины от величины деформации х является парабола.

1.5.5.3. Градиент скалярного поля

Скалярным полем называют область пространства, каждая точка которого характеризуется некоторой скалярной величиной, например, температурой, освещенностью или значением потенциальной энергии материальной точки в силовом поле.

F

Поверхностью уровня скалярного поля называют совокупность точек пространства, в которых скалярная величина имеет одно и то же значение. Например, поверхностью уровня потенциальной энергии тела в гравитационном поле Земли является сфера. На рис. 1.28

Рис. 1.28.

45

несколько таких поверхностей показаны пунктиром. Потенциальная энергия тела в гравитационном поле Земли определяется формулой Wп G Mmr , и

Wп const., когда r const.

При перемещении тела по поверхности уровня потенциальной энергии работа сил поля равна нулю, так как во всех точках поверхности Wп const , то есть F ds 0. А это означает, что проекция вектора силы на любое направ-

WП	WП		n
WП	n
				P s
	P0
			s

Рис. 1.29.

ление вдоль поверхности уровня равна нулю F 0 . Следовательно, вектор силы поля перпендикулярен к поверхности уровня потенциальной энергии.

Рассмотрим некоторое скалярное поле (рис. 1.29). При перемещении по направлению вектора s на величину s, мы переходим из точки P0, в которой потенциальная энергия равна Wп, в точку P, где потенциальная энергия имеет значение Wп+ Wп. Производной скалярного поля по направлению вектора s (частной производной) называют величину

Wп lim Wп .

s s 0 s

Эта величина характеризует изменение скалярного поля при перемещении на единицу длины в заданном направлении. В направлении нормали n к поверхности уровня изменение потенциальной энергии на единицу длины

принимает максимальное значение. Из рисунка 1.29 видно, что s n , n cos

– кратчайшее расстояние между поверхностями уровня, угол между век-

торами n и s . Тогда и	Wп	Wп cos .
	s	n

Введем понятие вектора градиента скалярного поля:

grad Wп ddnWп n ,

где n – единичный вектор, направленный в сторону максимального увеличения скалярного поля. Таким образом, градиент скалярного поля – это вектор, по модулю равный изменению скалярной величины (в данном случае потен-

46

циальной энергии) при перемещении на единицу длины в направлении нормали к поверхности уровня. Вектор градиента направлен перпендикулярно поверхности уровня в сторону возрастания скалярной величины.

1.5.5.4.Связь силы и потенциальной энергии

Каждой точке потенциального поля соответствует, с одной стороны, некоторое значение вектора силы F , действующей на тело, и, с другой стороны, некоторое значение потенциальной энергии Wп. Следовательно, между силой и потенциальной энергией должна существовать определенная связь.

При перемещении тела по нормали к поверхности уровня вдоль вектора градиента на величину dn совершается работа Fndn dWп . Отсюда видно, что проекция силы на направление градиента потенциальной энергии отрица-

тельна и по модулю равна этому градиенту Fn dWdnп .

Если учесть, что и вектор силы и вектор градиента направлены перпендикулярно к поверхности уровня, получим

F grad Wп ,

то есть вектор силы противоположен вектору градиента потенциальной энергии.

Потенциальная энергия может изменяться не только при перемещении вдоль нормали к поверхности уровня, но также и при перемещениях вдоль других направлений. Для любого направления в пространстве, в частности и для направлений декартовых координатных осей х, у, z:

F	Wп , F		Wп , F		Wп	.
x	x	y	y	z	z

Эти формулы определяют величины проекций вектора силы на координатные оси. Если известны все проекции, оказывается определенным и сам вектор силы:

		W	W	W
	F	п i	п j	п	k .
				z
		x	y

47

Сила равна градиенту потенциальной энергии, взятому с обратным знаком F grad Wп , тогда градиент потенциальной энергии в прямоугольных декартовых координатах имеет вид:

grad W Wп i Wп j Wп k .
п	x	y	z

Введѐм понятие оператора. Оператор, действующий над пространствами функций, это правило, согласно которому одна функция преобразуется в другую. Многие операции векторного анализа могут быть записаны в сокращѐнной и удобной форме с помощью символического оператора Гамильтона «набла» , обозначаемого знаком :

		i		j		k .
			y
	x				z

Оператор «набла» действует на те поля, что стоят от него справа, и не действует на поля, стоящие от него слева. В этом операторе соединены дифференциальные и векторные свойства. Будем понимать формальное ум-

	ножение		на функцию W	как частную производную	Wп , а в рамках век-
		x
			п		x

торной алгебры формальные операции над оператором будем проводить так, как если бы он был вектором. Если умножить вектор на скалярную

функцию		потенциальной				энергии	Wп	,	то	получится
W	Wп i Wп		j	Wп	k . Это вектор градиента потенциальной энергии.
п	x	y		z

В удобной и сокращенной форме его можно записать как grad Wп Wп , а вектор силы в виде:

F Wп .

Пример 1. Рассчитать градиент скалярного поля расстояния точек пространства до начала координат (градиент модуля радиус-вектора r ).

Решение:

48

В прямоугольной декартовой системе координат r x2 y2 z2 , тогда

r

r

i

r

j

r

k .

Взяв частные производные:

r

x2 y2 z2

x

y

z

,

x

x

r

2x

x

,

r

y

,

r

z

, получим, r

x

i

y

j

z

k , или

x

2 x2 y2 z2

r

y r

z

r

r

r

r

r 1r xi yj zk . Выражение, стоящее в скобках, представляет собой ра-

диус-вектор точки поля r xi yj zk , тогда

r rr .

Приходим к выводу: градиент скалярного поля расстояния точек пространства до начала координат есть безразмерный единичный вектор в направлении радиус-вектора точки поля.

Пример 2. Потенциальная энергия тела в поле гравитации планеты рав-

на Wп G Mmr . Используя связь силы поля с градиентом потенциальной энергии, определить вектор силы гравитации.

Решение:

		Mm
F Wп ,	F G			, где GMm постоянная величина r - переменная.
		r

Оператор набла проявляет дифференциальные свойства, и его действие очень

похоже			на			операцию		нахождения	дифференциала		функции
	Mm		G	Mm						d
d G							dr , только вместо символа дифференциала				ставится
					2
	r			r

	Mm			Mm
символ оператора «набла» . Тогда F G			G			r . Учитывая,
					2
	r			r

что r rr , окончательно получим:

F G Mm r . r2 r

Пример 3. Потенциальная энергия тела в поле тяготения Земли равна Wп mgy const . Определить вектор силы, действующий на тело.

						49
	Решение:
			W	W	W
	F Wп ,	F	п i	п j	п	k	,	F mgj . Орт оси y вектор j
					z
			x	y

направлен вертикально вверх (от поверхности Земли), тогда gj g есть вектор ускорения свободного падения, а вектор силы, действующий на тело, будет равен

F mg .

Наглядно картины силовых полей, соответствующие примерам 2 и 3, приведены на рис. 1.30. Также на этом рисунке показаны направления действущих сил и векторов градиента потенциальной энергии.

	y
	WП	WП dWП
WП n F	dy n		WП
	F
a	dr
		б
	Рис. 1.30.
Пример 4. Потенциальная энергия упругих сил равна W				kx2	. Найти проек-
		п	2

цию упругих сил на ось x.

Решение: F	Wп , F kx .
x	x	x

1.5.5.5. Потенциальная энергия взаимодействия