Математика для економістів Заоч. 2010 ч

x

0

x0

x0 + x

x

	Нехай f(x) визначена на деякому проміжку (a, b). Тоді tg					f	тангенс кута
						x
	нахилу січної МР до графіку функції.
	lim tg	lim	f	f (x0 ) tg	,
			x
	x 0	x 0

де - кут нахилу дотичної до графіку функції f(x) в точці (x0, f(x0)).

Кут між кривими може бути визначений як кут між дотичними, проведеними до

цих кривих в будь-якій точці.
Рівняння дотичної до кривої: y			y0	f (x0 )(x				x0 )
Рівняння нормалі до кривої: y			y0	1			(x	x0 ) .
					f (x0 )
Фізичний зміст похідної функції f(t), де t- час, а f(t)- закон руху (зміни
координат) – миттєва швидкість руху.
Відповідно, друга похідна функції – швидкість зміни швидкості, тобто
прискорення.
Односторонні похідні функції в точці
Означення. Правою (лівою) похідною функції f(x) в точці х = х0 називається
праве (ліве) значення границі відношення					f	при умові, що це співвідношення існує.
					x
f (x0 ) lim	f							f (x0 ) lim	f
	x								x
x 0								x 0

Якщо функція f(x) має похідну в деякій х = х0, то вона має в цій точці односторонні похідні. Однак, обернене твердження невірне. По-перше функція може мати розрив в точці х0, а по-друге, навіть якщо функція неперервна в точці х0, вона може бути в ній не диференційованою.

Наприклад: f(x)= x - має в точці х=0 і ліву і праву похідну, неперервна в цій точці,

однак, не має в ній похідної.

Теорема. (Необхідна умова існування похідної). Якщо функція f(x) має похідну в точці х0, то вона неперервна в цій точці.

Ця умова не є достатньою.

Основні правила диференціювання

Позначимо f(x) = u, g(x) = v- функції, диференційовані в точці х.

1) (u

v) = u

v ;

2) (u v) = u v + u v;

3)

u

u v

v u

, якщо v

0 ;

v

v2

Похідні основних елементарних функцій

1) С

= 0;

9)

sin x

cos x

2) (xm)

= mxm-1;

10)

cos x

sin x

3)

1

11)

tgx

1

x

cos2 x

2 x

1

1

12)

ctgx

1

4)

sin

2

x

x

x 2

5)

e x

e x

13)

arcsin x

1

1

x 2

6)

a x

a x ln a

14)

arccosx

1

1 x 2

7)

ln x

1

15)

arctgx

1

x

1

x2

8)

loga x

1

16)

arcctgx

1

x ln a

1

x2

Похідна складної функції

Теорема. Нехай y = f(x); u = g(x), причому область значень функції u входить в область визначення функції f.

Тоді y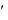f (u) u.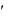

Логарифмічне диференціювання

ln x, при x

0

Розглянемо функцію y

ln

x

ln(

x),

при

x

0 .

Тоді (ln x ) =

1

, так як

ln x

1

;

(ln(

x))

(

x)

1

.

х

x

x

x

Враховуючи отриманий результат, можна записати:

g(x)

						f (x)	.
			ln	f (x)
		f (x)				f (x)
	Відношення		називається логарифмічною похідною функції f(x).
		f (x)

Метод логарифмічного диференціювання полягає в тому, що спочатку знаходять логарифмічну похідну функції, а потім похідну самої функції за формулою:

f (x) (ln f (x) ) f (x) .

Похідна показниково-степеневої функції

Функція називається показниковою, якщо незалежна змінна входить в показник степеня, і степеневою, якщо змінна є основою. Якщо ж і основа і показник степеня

залежать від змінної, то така функція буде показноково-степеневою.

Нехай u=f(x) и v=g(x) – функції, які мають похідні в точці х, f(x)>0.

Знайдемо похідну функції y=uv. Логарифмуючи, отримаємо:

lny = vlnu

		y	v ln u			v	u
		y					u
	y		u v v	u		v ln u
				u
	Звідки отримаємо:
	u v		vuv 1u u v v ln u .

Похідна обернених функцій

Нехай необхідно знайти похідну функції у = f(x) за умови, що обернена їй функція x = g(y) має похідну, відмінну від нуля у відповідній точці.

Для рішення цієї задачі диференціюємо функцію x 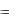по x :

1 g ( y) y ;

Так як g (y) 0	y	1		;
		g ( y)
			dy		1				,
			dx				dx
							dy

тобто похідна оберненої функції обернена по величині похідної даній функції.

Наприклад. Знайти формулу для похідної функції arctg.

Функція arctg є функцією, оберненою до функції tg, тобто її похідна може бути знайдена наступним чином:

y

tgx;

x

arctgy;

Відомо, що y

(tgx)

1

;

cos2 x

По наведеній вище формулі отримаємо:

y

1

;

d (arctgy)

1

.

d (arctgy) / dx

dy

1/ cos2 x

Так як

1

1 tg 2 x

1

y 2 ; то

можна

записати

кінцеву формулу для похідної

cos2 x

арктангенса:

(arctgy)

1

.

1

y 2

Таким чином отримані всі формули для похідних арксинуса, арккосинуса і

інших обернених функцій, наведених в таблиці похідних.

Диференціал функції

Нехай функція y= f(x) має похідну в точці х:

			lim	y		f (x) .
				x
			x 0
Тоді можна записати:	y	f (x)	, де			0, при х 0.
	x
Отже:	y f (x)		x	x .

Величина x - нескінченно мала більш високого порядку, ніж f (x) x, тобто f (x) x-

головна частина приросту	у.
Означення. Диференціалом функції f(x) в точці х називається головна лінійна
частина приросту функції.
Позначається dy або df(x).
Із означення слідує, що dy = f (x) x або
			dy = f (x)dx.
Можна також записати: f	(x)	dy	.

dx

Геометричний зміст диференціалу

y

f(x)

K

dy

M y L

x

x + x

x

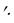З трикутника MKL: KL = dy = tg x = y x.

Таким чином, диференціал функції f(x) в точці х дорівнює приросту ординати дотичної до графіка цієї функції в розглядаємій точці.

Властивості диференціала

Якщо u = f(x) і v = g(x)- функції, диференційовані в точці х, то безпосередньо із означення диференціала слідують наступні властивості:

1) d(u v) = (u v) dx = u dx v dx = du dv

2)d(uv) = (uv) dx = (u v + v u)dx = vdu + udv

3)d(Cu) = Cdu

4) d	u		vdu udv
	v		v2

Диференціал складної функції

Інваріантна форма запису диференціалу

Нехай y = f(x), x = g(t), тобто у - складна функція.

Тоді	dy = f (x)g (t)dt = f (x)dx.

Форма запису диференціала dy не залежить від того, чи буде х незалежною змінною або функцією будь-якої іншої змінної, у зв‟язку з чим ця форма запису називається інваріантною формою запису диференціала.

Однак, якщо х - незалежна змінна, то dx = x, але якщо х залежить від t, то

хdx.

Таким чином, форма запису dy = f (x) x не є інваріантною.

Розкриття невизначеностей

Правило Лопіталя.

(Лопіталь (1661-1704) – французький математик)

До невизначеностей відносять наступні співвідношення:

0	;		; 0; 0 ; 1 ;	.
0

Теорема (правило Лопіталя). Якщо функції f(x) і g(x) диференційовані в околі точки а, неперервні в точці а, g (x) відмінна від нуля в околі а і f(a) = g(a) = 0, то границя відношення функцій при х а дорівнює границі відношення їх похідних, якщо ця границя (скінчена або нескінченна) існує.

lim f (x)

x a g(x)

lim f (x) .

x a g (x)

Наприклад. Знайти границю lim	x2 1		ln x	.
x 1	e	x	e

Як видно, при спробі безпосереднього обчислення границі отримаємо невизначеність

виду 00 . Функції, які входять в чисельник і знаменник дробу задовольняють вимогам теореми Лопіталя:

f (x) = 2x +

1

;

g (x) = ex;

х

2x

1

f (x)

2 1

3

lim

x

.

g (x)

e x

e

e

x 1

Якщо при розв‟язуванні прикладу після застосування правила Лопіталя спроба обчислити границю знову приводить до невизначеності, то правило Лопіталя може бути застосовано другий раз, третій і т.д. доки не буде отримано результату. Це можливо лише в тому випадку, коли знов отримані функції в свою чергу задовольняють вимогам теореми Лопіталя.

			x
Наприклад. Знайти границю lim		xe 2				.
	x		e		x
x

		x		1
					x) ;	g (x) 1 e x ;
	f (x) e 2 (1
				2

			1		x		1			x				x		x		1		x
								e							e				e			(4 x) ;					g (x) e x ;
		f (x)		e 2						2						2				2
			2				2							4			4
	1							1				x											1
f (x)		;	g (x)						e 2 ;											lim							0 .
	4						2																	x
																				x
																							2e 2
															Формула Маклорена

Одним із основних принципів математики є зображення складного через більш

простіше. Формула Маклорена є реалізацією цього принципу. Будь-які функції,

диференційовані достатню кількість разів в точці x 0 , можуть бути зображені у

вигляді многочленів деякого степеня. Останні є більш простими елементарними функціями, над якими зручно виконувати арифметичні дії, обчислювати значення в

будь-якій точці і т.д. Отже, функція						f (x) , яка має (n				1) похідну в точці x 0 , може
бути зображена за формулою Маклорена разом із залишковим членом:
f (x) f (0)	f '(0)	x	f ''(0)	x2			f (n) (0)	xn	O(x) .
	1!		2!				n!
Ця формула дає можливість зобразити функцію										f (x) у вигляді многочлена. Ця

формула широко використовується для наближених обчислень значень різних функцій; при цьому похибка обчислень оцінюється по залишковому члену розкладення O(x) .

Приклади

x 2 e x2

1. Знайти похідну функції y

.

x 2 1

Розв'язок.

y

(2xex2

x 2 2xex2 )(x 2 1) (2x)x 2 e x2

2x3e x2

2x5 e x2

2xex2

2x3e x2

2x3e x2

(x 2

1)2

(x 2 1)

2

2. Знайти

2xex2 (x 4

1 x 2 )

.

(x 2

1)2

похідну функції y

ln tg

x

x

.

2

sin x

Розв'язок.

y

1

1

1

sin x

x cos x

1

sin x

x cos x

sin x

sin x

x cos x

tg

x

cos

2

x

2

sin2 x

2sin

x

cos

x

sin2 x

sin2 x

2

2

2

2

3. Знайти

x cos x

sin2 x

похідну функції y

arctg

2x4

.

1

x8

y

1

8x3 (1 x8 ) ( 8x7 )2x 4

(1 x8 )2 (8x3 8x11

16x11 ) 8x3

8x11

1

4x8

(1 x8 )2

(1 x8 )2 (1 x8 )2

(1 x8 )2

(1

x8 )2

4. Знайти

8x3 (1

x8 )

8x3

(1 x8 )2

1

x8

похідну функції y

x2 e x2

ln x

y

x

2

e

x2

ln x

x

2

e

x2 1

2xe

x2

x

2

e

x2

2x ln x

xe

x2

2xe

x2

(1

x

2

) ln x xe

x2

x

5. Знайти

xex2 (1 2 ln x 2x 2 ln x)

похідну функції

f (x)

(x 2

3x) x cos x .

Розв'язок.

По

формулі

показниково-степеневої

функції

отримаємо:

u

x 2

3x;

v x cos x;

Похідні цих функцій: u

2x 3;

v

cos x

xsin x;

Отже:

f

(x)

x cos x

(x 2

3x) x cos x 1 (2x

3)

(x 2

3x) x cos x (cos x

x sin x) ln(x 2

3x) .

6. Продиференціювати вказані функції:

а) f (x)

ln(cos

x 1) ,

Розв'язок.

1

1

tg

x

1

,

f

(x)

sin

x

1

cos

x

1

2

x

1

2

x

1

	b)	x		5 sin 2t					3sin 3t,	:
		y 3 cos2t							2 cos3t
	Розв' язок.
	xt	10 cos2t					9 cos3t,
	yt	6 sin 2t					6 sin 3t			6 sin 2t sin 3t ,
	f	x	dy			yt		;
			dx			xt
	f	x		6 sin 2t					sin 3t	.
			10 cos2t						9 cos3t

с) x2 xy				y2ex	0,
	2x y xy 2 yy ex ex y2 0,
	2x y ex y2					y x 2 yex ,
Розв' язок :
y		2x	y	ex y	2	.
		x	2 yex

7. Розкласти функцію по формулі Маклорена: f (x) ex .

Розв'язок. Оскільки має вигляд:

e(n) (x) ex , f (n) (0) e0 1 то для будь-якого n , формула Маклорена

			x		x2		x3		xn
ex	1									o(xn ) .
		1!			2!	3!			n!
Ця формула використовується для					обчислення				числа e з будь-якою необхідною

точністю. Звідси при x 1 отримаємо наближене значення числа e 2,71882818 .

Завдання

1. Знайти похідні функції вигляду у=хn, у= ах, у=loga x (у=lnх).

В. 1

В. 2

1.

y 1 2x 30 , y ?

1. y 1 x2 10 , y ?

2. y

x3

2x

, y ?

2. y x3

102 x 3 , y ?

e x

3.

y

x2 log3 x,

y ?

3.

y

ln 2 x,

y

?

x

1

4.

y

t 3

1 t,

y (0) ?

4.

y

,

y (2) ?

x

1

В. 3

В. 4

1.	y 1 x 20 , y ?														1.	y x2					1 4 , y ?
2.	y e x 1 , y ?														2. y				1 e3x , y ?
3.	y			x		1			,	y		?			3.	y		log			x3					1 ,		y	?
				log2 x															3
4.	y	1				x2				5		1		, y ?	4.	y			1	x2			,				y (0) ?
											x2
																			1	x2
		В. 5															В. 6
1.	y x3						x 6 , y ?								1.	y 5x2					3 7 , y ?
2.	y 23x , y ?														2.	y 3x 23x , y ?
3.	y ln x 2								4x , y ?						3.	y		ln x			, y ?
																	1		x2
4.	y		2			x		,		y (1)		?			4.	y			3				x2				,	y (2)	?
		1				x2											5		x		5

2. Знайти похідні тригонометричних функцій і обернених тригонометричних

функцій.

В. 1

В. 2

1.

y

2sin x

,

y

?

1.

y

sin 3x

,

y ?

2sin2 x

cos x

cos2x

x

2.

y

tg

,

y

?

2.

y

ctg3 1 x2 ,

y

?

2

3.

y

(arcsin x)2 ,

y

?

3.

y

arcsin x

, y

?

arccosx

4.

y

x

arctgx,

y ?

4.

y

arctgx3 ,

y

?

1 x2

В. 3

В. 4