
Математика для економістів Заоч. 2010 ч
.1.pdf
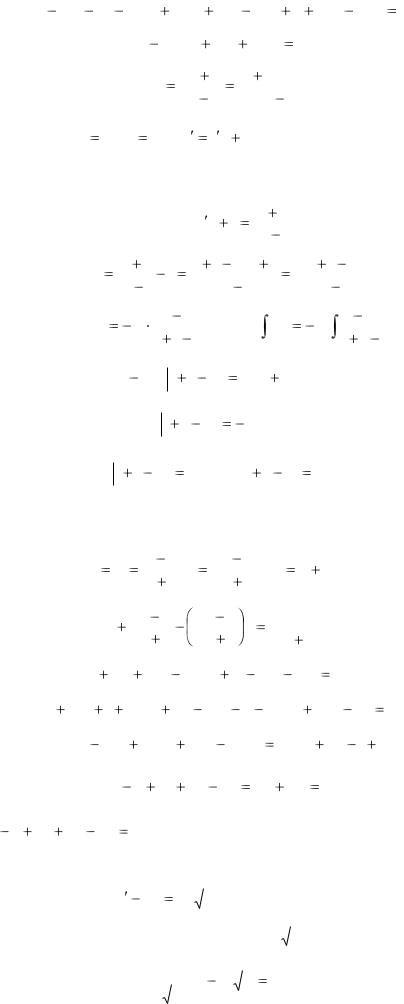
(u 1/ 5 |
|
2v |
14/ 5 |
|
|
3)dv |
|
|
(2u |
2 / 5 |
|
|
|
v |
7 / 5 1)du |
0; |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
(u |
2v)dv (2u |
v)du |
|
0; |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dv |
|
|
|
2u |
|
|
v |
|
|
|
2 |
|
v / u |
|
; |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
du |
|
|
|
2v |
|
|
u |
|
|
|
2v / u 1 |
|
|
|
|
|
|
||||||||||||||
Замінимо змінну |
|
v |
|
|
t; |
v |
ut; |
v |
|
|
t u |
|
t; |
|
при |
підстановці |
у вираз, записаний |
|||||||||||||||||||||||||
|
u |
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
вище, маємо: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t u |
|
|
t |
|
2 |
|
|
t |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2t |
1 |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Розділимо змінні: |
dt |
|
u |
2 |
|
|
|
t |
|
t |
2 |
|
|
t |
|
|
2t 2 |
|
|
|
t |
|
2(1 t |
|
t 2 ) |
; |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
du |
2t |
1 |
|
|
|
|
|
|
|
|
|
2t |
|
1 |
|
|
|
|
|
|
|
|
|
2t |
1 |
|
|
||||||||||||||
|
|
|
|
du |
|
|
1 |
|
|
|
1 |
2t |
|
|
dt; |
|
|
|
|
|
du |
|
|
|
1 |
|
|
(1 2t)dt |
; |
|||||||||||||
|
|
|
|
|
u |
|
2 1 t t 2 |
|
|
|
|
|
u |
|
|
2 1 t t 2 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
ln1 |
t |
|
|
|
|
|
ln |
u |
|
|
ln C |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ln1 |
t |
|
|
|
|
|
2 ln |
C u |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln1 t |
|
|
t |
2 |
|
|
ln |
|
C2 |
|
; |
|
1 |
|
t |
|
t |
2 |
C2 |
; |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
u 2 |
|
|
|
|
|
|
u 2 |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Переходимо тепер до початкової функції у і змінної х.
|
t |
|
v |
|
|
y 7 / 5 5y 7 |
; u x 1/ 5; |
|||||||||||||||||||||||
|
|
u |
|
|
x |
1/ 5 |
|
|
|
|
5x |
1 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
1 |
|
5y |
7 |
|
|
|
|
|
5y |
7 |
|
2 |
|
|
25C2 |
|
; |
|||||||||||
|
|
|
5x 1 |
|
|
|
|
5x 1 |
|
|
(5x 1)2 |
|||||||||||||||||||
|
(5x |
1)2 |
|
(5 y 7)(5x 1) |
|
(5 y |
7)2 |
|
25C2 |
|||||||||||||||||||||
25x 2 |
10x |
1 25xy |
|
5 y |
|
|
35x |
7 |
25y 2 |
70y 49 25C2 |
||||||||||||||||||||
|
25x 2 |
25x |
25xy |
|
|
|
75y |
|
25y 2 25C2 |
49 1 7 |
||||||||||||||||||||
|
|
x2 |
x xy 3y y 2 |
|
C2 |
55 |
C; |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
25 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Отже, вираз x 2 x xy |
3y |
y 2 |
C є загальним інтегралом заданого диференціального |
|||||||||||||||||||||||||||
рівняння. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8. Розв‟язати рівняння xy |
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
4 y |
|
|
|
|
y. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Розв'язок. Розділимо обидві частини рівняння на x |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
y. |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
dy |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
x. |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
y dx |
|
x |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
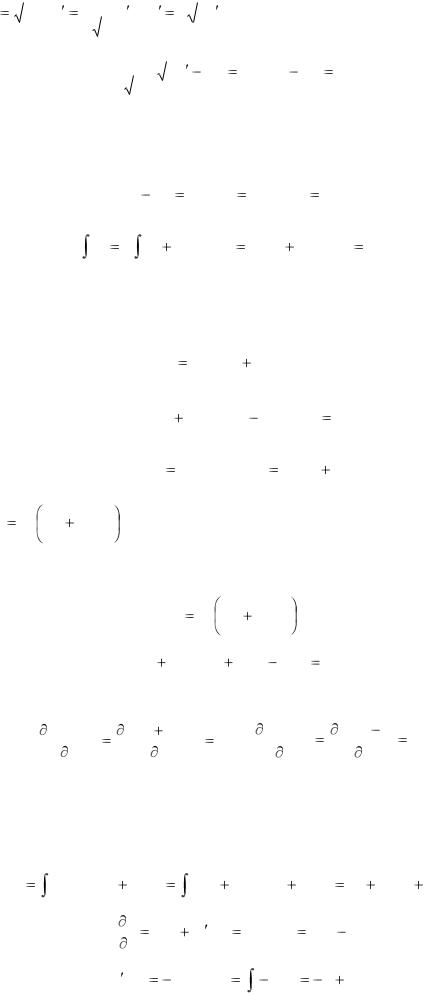
Покладемо z |
|
|
|
1 |
|
|
|
|
|
|
y; z |
|
|
|
y ; y 2 y z ; |
||||||
|
|
|
|
|
||||||
|
|
|
|
|
||||||
|
|
|
||||||||
|
2 |
|
|
y |
||||||
1 |
|
|
|
|
4 |
z x; |
dz 2z |
|
x |
|
|||
|
2 y z |
; |
|||||||||||
|
|
|
|
|
|
|
|
|
|||||
|
y |
x |
dx x |
2 |
|
||||||||
Отримали лінійне неоднорідне диференціальне рівняння. Розглянемо відповідне йому лінійне однорідне рівняння:
|
|
dz |
|
|
2z |
0; |
|
dz |
|
2z |
; |
dz 2dx |
; |
||||
|
|
dx |
|
|
x |
|
dx |
|
x |
z |
|
|
x |
||||
|
|
|
|
|
|
|
|
|
|||||||||
dz |
2 |
|
dx |
C ; |
ln z |
2 ln x |
ln C; |
z |
Cx 2 ; |
||||||||
|
|
|
|
|
|
||||||||||||
z |
|
|
x |
1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Вважатимемо, що C=C(x) і підставляємо отриманий результат в лінійне неоднорідне рівняння, з урахуванням того, що
|
dz |
|
2xC(x) x |
2 |
dC(x) |
; |
|
|
||||||||
|
dx |
|
|
|
dx |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2xC(x) x |
2 dC(x) 2x2C(x) |
x |
; |
|||||||||||||
|
|
dx |
|
|
|
x |
|
|
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
dC(x) |
|
|
1 |
|
; |
C(x) |
|
1 |
ln x C2 ; |
|||||||
dx |
|
|
|
2 |
||||||||||||
|
2x |
|
|
|
|
|
|
|
|
|||||||
Отримаємо: z x2 C |
|
1 |
ln x ; |
|
2 |
2 |
|||
|
|
|||
|
|
|
Застосовуючи зворотну підстановку, отримаємо кінцеву відповідь:
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
y x 4 C |
|
1 |
ln x |
|
|
|
|
|
|
2 |
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
9. Розв‟язати рівняння (3x 2 10xy)dx |
(5x 2 1)dy |
0 |
|
|||||||
Розв'язок. Перевіримо умову тотальності: |
|
|
|
|
|
|
||||
|
M (x, y) |
|
(3x 2 10xy) |
10x; |
N (x, y) |
|
(5x2 1) |
10x. |
||
|
y |
|
y |
|
x |
|
x |
|||
|
|
|
|
|
|
|
||||
Умова тотальності виконується, отже, диференціальне рівняння є рівнянням в повних диференціалах.
Визначимо функцію u.
u M (x, y)dx C( y) |
(3x2 |
10xy)dx C( y) x3 5x2 y C( y); |
|||
|
u |
5x2 C ( y) N (x, y) 5x2 1; |
|||
|
|
|
|||
|
y |
||||
|
|
|
|
||
C ( y) |
|
1; C( y) |
( 1)dy y C1 ; |
||

Отже, u x3 5x 2 y
Знаходимо загальний інтеграл заданого диференціального рівняння:
u x3 |
5x |
2 y y C С |
;. |
|
|
|
1 |
2 |
|
x3 |
5x 2 y y C. |
|
|
|
Завдання
1. Розв‟язати диференціальне рівняння:
а) xy' |
y y2 |
y 1 2 ; |
|
б) |
|
dy |
|
y |
|
x |
; в) |
y' 3y e 2 x ; |
|||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
dx x |
|
y |
|
|
|
|
|||||
г) y' |
yx |
exp( |
x2 / 2) ; д) |
x2 dy |
(xy y 2 )dx . |
|
|
|
|
||||||||||||
|
2.Знайти частинний розв‟язок рівняння, , який задовольняє початкову умову: |
||||||||||||||||||||
а) xy' |
1 |
y 2 , y(1)=0; б) yy' |
x |
0 |
, y |
|
x 0 |
1, в) y' |
1 |
y2 |
, y(0)=1; |
||||||||||
|
|||||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
1 |
x2 |
|||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
2x4 , у(2)=8. |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
г) y |
xy' |
, y(1) |
|
5 ; д) xy' |
2 y |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Питання для самоконтролю
11.Яке диференціальне рівняння називається звичайним?
12.Що називається диференціальним рівнянням першого порядку?
13.Що називається розв‟язком диференціального рівняння?
14.Дати означення загального та частинного розв‟язків диференціального рівняння першого порядку.
15.Сформулювати теорему Коші про існування та єдність розв‟язку рівняння першого порядку.
16.Дати означення рівняння з відокремлюваними змінними. Як воно розв‟язується?
17.Дати означення лінійного рівняння першого порядку та викласти метод його інтегрування.
18.Навести рівняння, звідні до лінійних та викласти методи їх інтегрування.
19.Дати означення рівняння Бернуллі. Як воно розв‟язується?
20.Які методи розв‟язування лінійних рівнянь ви знаєте?
Тема 13. Економічна динаміка та її моделювання: диференціальні та
різницеві рівняння

Мета заняття. Вивчення теми надасть студентам можливість знати диференціальні рівняння другого і вищих порядків, їх види та методи розв‟язування.
А також вивчити комплексні числа.
План заняття
1.Комплексні числа.
2.Диференціальні рівняння вищих порядків. Означення.
3.Рівняння, що допускають зниження порядку.
4.Лінійні однорідні диференціальні рівняння зі сталими коефіцієнтами.
5.Лінійні неоднорідні диференціальні рівняння зі спеціальною правою частиною.
Методичні рекомендації до практичного заняття
Комплексні числа |
|
|||||
Означення. Комплексним числом z називається вираз z |
a ib , де a і b – дійсні |
|||||
числа, i – уявна одиниця, яка визначається співвідношенням: |
|
|||||
i2 |
|
|
|
|
|
|
1; |
i |
1. |
|
|||
При цьому число a називається дійсною частиною числа z (a=Rez), а b- уявною |
||||||
частиною (b = Im z). |
|
|
|
|
|
|
Означення. Числа z a ib і z a |
ib називаються комплексно – спряженими. |
|||||
Означення. Два комплексних |
числа |
z1 |
a1 ib1 і z2 |
a2 ib2 називаються |
||
рівними, якщо відповідно рівні їх дійсні і уявні частини: |
|
|||||
a1 |
a2 ; |
b1 |
|
b2 ; |
|
|
Означення. Комплексне число дорівнює нулю, якщо відповідно дорівнюють нулю дійсна і уявна частини.
a b 0.
Диференціальні рівняння вищих порядків
Означення. Диференціальним рівнянням порядку n називається рівняння виду:
F (x, y, y ,..., y (n) ) 0
В деяких випадках це рівняння можна розв‟язати відносно y(n):
y (n) |
f (x, y, y ,..., y (n 1) ). |

Так само як і рівняння першого порядку, рівняння вищих порядків мають
нескінченну кількість розв‟язків. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Означення. Розв‟язок y |
(x) |
задовольняє початковим умовам x |
, y |
, y |
,..., y(n 1) , |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
0 |
|
0 |
якщо (x |
) |
y |
, |
(x |
) |
y |
, .... |
, |
|
(n 1) (x |
) |
y(n 1) . |
|
|
|
|
|
|
||
0 |
|
0 |
|
0 |
|
0 |
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
Означення. |
Знаходження |
|
розв‟язку |
рівняння F (x, y, y ,..., y (n) ) |
0 , |
що |
||||||||||||||
задовольняє початковим умовам x |
, y |
, y |
,..., y(n 1) , називається розв’язком задачі Коші. |
|||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
0 |
0 |
|
|
0 |
|
|
|
|
|
|
Теорема Коші. (Теорема про необхідні і достатні умови існування розв‟язку |
||||||||||||||||||||
задачі Коші). Якщо функція (n-1)–й змінних виду |
f (x, y, y ,..., y (n 1) ) в деякій області D |
|||||||||||||||||||
(n-1)- вимірного простору неперервна і має неперервні частинні похідні по y, y ,..., y (n 1)
, |
то якою б не була точка ( x |
, y |
0 |
, y |
0 |
,..., y(n 1) ) в цій області, існує єдиний розв’язок |
|
|
0 |
|
|
|
0 |
||
y |
(x) рівняння y (n) f (x, y, y ,..., y (n 1) ) , |
визначеного в деякому інтервалі, який |
|||||
містить точку х0, який задовольняє початковим умовам x0 , y0 , y0 ,..., y0(n 1) .
Диференціальні рівняння вищих порядків, розв‟язок яких може бути знайдено аналітично, можна розділити на декілька основних типів.
Рівняння, що допускають пониження порядку Пониження порядку диференціального рівняння – основний метод розв‟язку
рівнянь вищих порядків. Цей метод дає можливість порівняно легко знаходити розв‟язок, однак, він застосовується далеко не до всіх рівнянь. Розглянемо випадки,
коли можливе зниження порядку.
Рівняння виду y(n) = f(x)
Якщо f(x) – функція неперервна на деякому проміжку a<x<b, то розв‟язок може бути знайдено послідовним інтегруванням:
y(n 1) 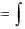 f (x)dx C1 ;
f (x)dx C1 ;
y(n 2) |
f (x)dx C dx C |
2 |
dx f (x)dx C x C |
; |
|
|
1 |
1 |
2 |
|
|
…………………………………………………………….
y |
dx dx.... f (x)dx C1 |
x n 1 |
|
C2 |
x n |
2 |
|
... Cn . |
(n 1)! |
|
(n |
2)! |
|||||
Рівняння, які не містять явно шуканої функції і їх похідних до порядку k – 1
включно
Це рівняння виду: F (x, y (k ) , y (k 1) ,..., y (n) ) 0.

В рівняннях такого типу можливе зниження порядку на k одиниць. Для цього роблять заміну змінної:
y (k ) z; |
y (k 1) z ; ... y (n) z (n k ) . |
Тоді отримаємо: F (x, z, z ,..., z (n k ) ) |
0. |
Тепер припустимо, що отримане диференціальне рівняння проінтегровано і сукупність його рішень виражається співвідношенням:
z 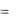 (x, C1 , C2 ,..., Cn k ).
(x, C1 , C2 ,..., Cn k ).
Роблячи зворотну підстановку, маємо:
y(k ) (x,C ,C |
,..., C |
n k |
) |
1 2 |
|
|
Інтегруючи отримане співвідношення послідовно k раз, отримаємо кінцеву відповідь:
y 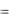 (x, C1 , C2 ,..., Cn ).
(x, C1 , C2 ,..., Cn ).
Рівняння, яке не містить явно незалежної змінної
Це рівняння виду F ( y, y ,..., y (n) ) |
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Порядок таких рівнянь може бути понижено на одиницю за допомогою заміни |
|||||||||||||||||||||||||
змінних y p. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
dy |
dy |
dy |
|
dp |
p; |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
dx |
dy |
dx |
|
dy |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
dp |
p |
|
|
|
|
|
|
2 |
|||
|
dy |
|
dy |
|
dy |
|
dy |
|
|
|
|
|
|
|
d 2 p |
|
dp |
||||||||
y |
|
|
|
|
|
p |
|
|
dy |
|
|
p |
|
p 2 |
p; і т.д. |
||||||||||
dx |
|
dy |
|
dx |
|
dy |
|
|
|
|
dy |
|
|
|
dy2 |
dy |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Підставляючи ці значення в початкове диференціальне рівняння, отримаємо:
F y, p, |
dp |
,..., |
d n 1 p |
0 |
|
|
|||
1 |
dy |
|
dyn 1 |
|
|
|
|
||
Якщо це рівняння проінтегрувати, і |
Ф( y, p, C1 , C2 ,..., Cn 1 ) 0 - сукупність його |
|||
рішень, то для розв‟язку даного диференціального рівняння лишається розв‟язати рівняння першого порядку:
Ф( y, y , C1 , C2 ,..., Cn 1 ) 0.
Лінійні диференціальні рівняння вищих порядків
Означення. Лінійним диференціальним рівнянням n – го порядку називається будь-яке рівняння першого степеня відносно функції у і її похідних y , y ,..., y (n) виду:
,..., y (n) виду:

p |
0 |
y(n) |
p y(n 1) |
p |
2 |
y(n 2) |
... p |
n 1 |
y |
p |
n |
y f (x); |
|
|
1 |
|
|
|
|
|
|
де p0, p1, …,pn – функції від х або постійні величини, причому p0 0.
Ліву частину цього рівняння позначимо L(y).
p |
y(n) |
p y(n 1) |
p |
2 |
y(n 2) ... p |
n 1 |
y |
p |
n |
y |
L( y); |
|
0 |
|
1 |
|
|
|
|
|
|
|
|||
Означення. Якщо f(x) = 0, то рівняння L(y) = 0 називається лінійним |
||||||||||||
однорідним рівнянням, якщо f(x) |
0, |
то рівняння L(y) = |
f(x) називається лінійним |
|||||||||
неоднорідним рівнянням, якщо всі коефіцієнти p0, p1, p2, … pn – постійні числа, то рівняння L(y) = f(x) називається лінійним диференціальним рівнянням вищого порядку з постійними коефіцієнтами.
Загальний розв‟язок лінійного однорідного диференціального рівняння другого порядку
Теорема. Якщо задано рівняння виду y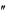 p1 (x) y
p1 (x) y p2 (x) y 0 і відомий один ненульовий розв’язок у = у1, то загальний розв’язок може бути знайдено за формулою:
p2 (x) y 0 і відомий один ненульовий розв’язок у = у1, то загальний розв’язок може бути знайдено за формулою:
y C |
|
y |
1 |
e |
p1 |
( x)dx |
dx C y . |
|
2 |
|
|
|
|||||
|
1 |
y 2 |
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
Лінійні однорідні диференціальні рівняння з постійними коефіцієнтами
Розв‟язок |
диференціального |
|
рівняння |
виду |
y(n) a y |
(n 1) ... a |
n |
y 0 або, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
скорочено, L(y) |
0 будемо шукати у вигляді y |
ekx , де k = const. |
|
|
|
||||||||||||
Так як y |
kekx ; |
y |
k 2 ekx ; ... |
|
y (n) |
k n ekx , |
то |
|
|
|
|
|
|
|
|
||
|
|
|
|
L(ekx ) |
ekx (k n |
a k n 1 ... |
a |
n |
). |
|
|
|
|||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
При цьому многочлен F(k) |
k n |
a k n 1 ... |
a |
n |
називається характеристичним |
||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
многочленом диференціального рівняння. |
|
|
|
|
|
|
|
|
|
|
|
||||||
Для того, |
щоб функція y |
ekx |
була розв‟язком початкового диференціального |
||||||||||||||
рівняння, необхідно і достатньо, щоб |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
L(ekx ) |
0; |
тобто ekx F (k) |
0. |
|
|
|
|||||||
Так як ekx |
0, то |
F(k) |
0 |
- |
це |
рівняння |
називається |
характеристичним |
|||||||||
рівнянням. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Алгебраїчне рівняння степеня n, характеристичне рівняння k n a k n 1 |
... a |
n |
0 |
1 |
|
|
має n коренів. Кожному кореню характеристичного рівняння ki відповідає розв‟язок диференціального рівняння.
В залежності від коефіцієнтів k характеристичне рівняння може мати або n
різних дійсних коренів, або серед дійсних коренів можуть бути кратні корені, можуть бути комплексно – спряжені корени, як різні, так і кратні.
Сформулюємо загальне правило знаходження розв‟язку лінійного однорідного диференціального рівняння з постійними коефіцієнтами.
1)записуємо характеристичне рівняння і знаходимо його корені.
2)знаходимо частинні розв‟язки диференціального рівняння, причому:
a) кожному дійсному кореню відповідає розв‟язок ekx;
б) кожному дійсному кореню кратності m ставиться у відповідність m
розв‟язків:
ekx ; xekx ; ... x m 1ekx .
в) |
кожній парі |
комплексно |
– |
спряжених |
коренів |
i характеристичного |
|||
рівняння ставиться у відповідність два розв‟язки: |
|
|
|
||||||
|
e x cos |
x і |
e x sin x . |
|
|
|
|
|
|
г) |
кожній |
парі |
m – кратних комплексно – спряжених коренів |
i |
|||||
характеристичного рівняння ставиться у відповідність 2m розв‟язків: |
|
||||||||
|
|
e x cos x, |
xe x cos |
x, |
... xm 1e x cos |
x, |
|
|
|
|
|
e x sin |
x, |
xe x sin |
x, |
...xm 1e x sin x. |
|
|
|
3) записуємо лінійну комбінацію знайдених розв‟язків.
Ця лінійна комбінація і буде загальним розв‟язком початкового лінійного однорідного диференціального рівняння з постійними коефіцієнтами.
Лінійні неоднорідні диференціальні рівняння з постійними коефіцієнтами Рівняння з правою частиною спеціального виду
Розрізняють наступні випадки:
I. Права частина лінійного неоднорідного диференціального рівняння має
вигляд:
|
|
|
f (x) P(x)e x , |
де P(x) A xm |
A xm 1 ... |
A |
- многочлен степеня m. |
0 |
1 |
m |
|

Тоді частинний розв‟язок шукається у вигляді:
y x r e x Q(x) ,
де Q(x)- многочлен того ж степеня, що і P(x), але з невизначеними коефіцієнтами, а r
– число, яке показує скільки раз число є коренем характеристичного рівняння для
відповідного лінійного однорідного диференціального рівняння (див. приклади).
II. Права частина лінійного неоднорідного диференціального рівняння має
вигляд:
f (x) e x P1 (x) cos x P2 (x) sin x ,
де Р1(х) і Р2(х) – многочлени степеня m1 і m2 відповідно.
Тоді частинний розв‟язок неоднорідного рівняння буде має вигляд:
y x r e x Q (x) cos x Q |
(x) sin x |
|
1 |
2 |
|
де число r показує скільки раз число |
i є коренем характеристичного рівняння для |
|
відповідного однорідного рівняння, а Q1(x) і Q2(x) – многочлени степеня не вище m,
де m- більша із степенів m1 і m2.
Відмітимо, що якщо права частина рівняння є комбінацією виразів розглянутих вище видів, то розв‟язок знаходиться як комбінація розв‟язків допоміжних рівнянь,
кожне з яких має праву частину, яка відповідає виразу, що входить в комбінацію.
Тобто, |
якщо рівняння має вигляд: L( y) |
|
|
f1 (x) f2 (x) , |
то частинний розв‟язок |
|||||||||||||||||||||||
цього рівняння буде |
y y1 |
y2 , |
|
де |
у1 і у2 – частинні розв‟язки допоміжних рівнянь |
|||||||||||||||||||||||
(див. приклади) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
L( y) |
|
f1 (x) и L( y) |
|
|
f2 (x) . |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Приклади |
|
|
|
|
|
|
||||||||||
1. |
Розв‟язати |
рівняння |
y |
|
|
e2 x |
|
з |
|
початковими |
умовами x0=0; y0=1; |
|||||||||||||||||
y0 1; |
y0 |
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
e |
2 x |
dx |
C |
|
1 |
e |
2 x |
C ; |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
y |
|
|
1 |
e |
2 x |
|
C |
dx |
|
1 |
e |
2 x |
C x |
C |
; |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
4 |
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
y |
1 |
|
e |
2 x |
C x C |
|
1 |
e |
2 x |
|
|
|
1 |
C x |
2 |
C |
x C |
; |
|||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
4 |
|
|
|
|
1 |
|
|
|
8 |
|
|
|
|
|
|
2 |
1 |
|
2 |
3 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Підставимо початкові умови:
