Математика для економістів Заоч. 2010 ч

Так само застосовуються методи підстановки (заміни змінної), метод інтегрування частинами, ті ж самі прийоми знаходження первісних для тригонометричних, ірраціональних і трансцендентних функцій. Особливістю є лише те, що при застосуванні цих прийомів потрібно розповсюджувати перетворення не лише на підінтегральну функцію, але і на границі інтегрування. Замінюючи змінну інтегрування, не забути змінити відповідно границі інтегрування.

Заміна змінних

b

Нехай задано інтеграл

f (x)dx , де f(x) – неперервна функція на відрізку [a,b] .

a

Введемо нову у відповідності з формулою x =

(t).

Тоді якщо

1)

(

) = а,

( ) = b

2)

(t) і

(t) неперервні на відрізку [ ,

]

3) f(

(t)) визначена на відрізку [ ,

], то

b

f (x)dx

f [ (t)] (t)dt

a

Тоді

F(a) .

f [

(t)]

(t)dt

F[

(t)]

F[ (

)] F[

( )]

F(b)

Інтегрування частинами

Якщо функції u

=

(x) і

v =

(x)

неперервні

на відрізку [a,b] , а також

неперервні на цьому відрізку їх похідні, то справедлива формула інтегрування частинами:

b	b	b
udv uv		vdu.
a	a	a

Наближене обчислення визначеного інтегралу Існує велика кількість функцій, інтеграл від яких не може бути виражено через

елементарні функції. Для знаходження інтегралів від таких функцій застосовують різноманітні наближені методи, суть яких полягає в тому, що підінтегральна функція замінюється “близькою” до неї функцією, інтеграл від якої виражається через елементарні функції.

Формула парабол

(формула Сімпсона або квадратурна формула)

(Томас Сімпсон (1710-1761)- англійський математик)

Розділимо відрізок інтегрування [a,b] на парне число відрізків (2m). Площа криволінійної трапеції, обмеженої графіком функції f(x) замінимо на площу криволінійної трапеції, обмеженої параболою другого степеня з віссю симетрії,

паралельній осі Оу і яка проходить через точки кривої, зі значеннями f(x0), f(x1), f(x2).

Для кожної пари відрізків побудуємо таку параболу. Рівняння цих парабол мають вид Ax2 +Bx + C, де коефіцієнти А, В, С можуть бути легко знайдені за трьома точками перетину параболи з початковою кривою.

у

0 х0 х1 х2 х3 х4 х

								y	0	Ax 2				Bx	0	C
												0
								y		Ax 2				Bx C
								1				1		1
								y	2	Ax 2				Bx	2	C
												2
Позначимо 2h x2		x0 .
x2				3	B x		2		Cx		x
S ( Ax 2 Bx C)dx A x												2
		3			2
x	0										x0
Якщо взяти х0 = -h, x1 = 0, x2 = h, то S													h	(2Ah 2		6C) .
													3

Тоді рівняння значень функції мають вигляд:

y0 Ah 2 Bh C y1 C

y2 Ah 2 Bh C

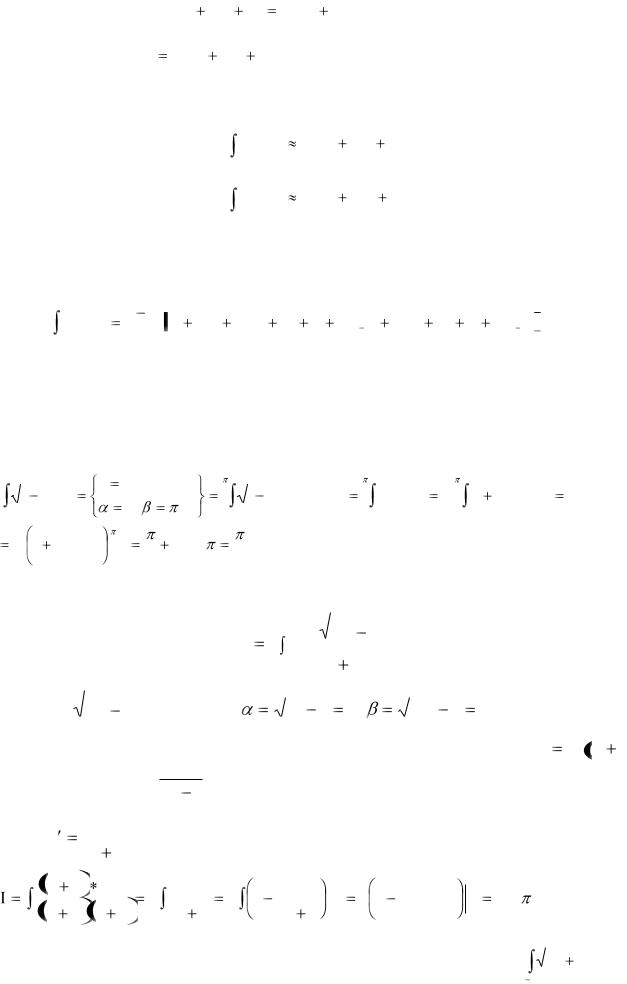
З урахуванням цього: y

0

4y

y

2

2Ah2

6C .

1

Звідки маємо:

S

h

( y

4 y

y

)

0

2

3

1

Тоді

x2

h

f (x)dx

( y

4 y

y

)

0

2

3

1

x0

x2

h

f (x)dx

( y

4 y3

y4 )

3

2

x2

.......... .......... .......... .......... .......

Додаючи ці вирази, отримаємо формулу Сімпсона:

b

b a

f (x)dx

y

y

2( y

y

... y

)

4( y

y

... y

) .

0

2m

2

4

2m 2

3

2m 1

6m

1

a

Чим більше взяти число m, тем більш точне значення інтегралу буде отримано.

Приклади

1. Обчислити визначений інтеграл

1								x	sin t;						/ 2										/ 2				1		/ 2
1				x2 dx					0;				/ 2			1 sin2 t costdt									cos2 tdt						(1 cos2t)dt
																													2
0															0										0						0
	1				1				/ 2				1
				t			sin 2t							sin			.
2					2						4		4		4
									0
2. Обчислити визначений інтеграл:
																		ln5 e x e x							1
																I											dx.
																					e x			3
															0
								e x
Нехай									1 =		t,		звідки						e0		1			0,				eln 5	1		2 . Отже, якщо х

змінюється від 0 до ln5, то нова змінна t змінюється від 0 до 2. Функція x ln t 2 1,

обернена до функції t e x 1 , на відрізку [0; 2] є монотонною і неперервною разом

з похідною x			2t			на цьому відрізку. Маємо:
			t 2	1
2	t 2	1 t 2tdt				2 t 2 dt		2		4				t
						2		2 1				dt	2 t 2arctg
0	t 2	4 t 2		1		0 t 2 4		0	t 2		4			2

2

0

4 .

	8
3. Обчислити наближене значення визначеного інтеграла		x3 16dx за
	2

формулою Сімпсона, розбивши відрізок інтегрування на 10 частин.

За формулою Сімпсона отримаємо:

	8				8		2
		x3	16dx					[ y(	2)	y(8) 2[ y(0) y(2) y(4) y(6)]
	2					6	5
	4[ y(		1) y(1)				y(3)		y(5)	y(7)]].

	m			0		1				2		3	4	5	6	7	8	9	10
	x			-2		-1				0		1	2	3	4	5	6	7	8
	f(x)			2.828		3.873				4		4.123	4.899	6.557	8.944	11.874	15.232	18.95	22.98
	8						8	2
		x3		16dx					[2.828			22.978 2[4		4.899	8.944	15.232]	4[3.873	4.123	6.557
	2					6		5
	11.874				18.947]]				91.151

Точне значення цього інтеграла – 91.173.

Завдання

1. Обчислити інтеграли:

	1				xdx						1											1 e x xdx;
1.							;			2.		1					xdx;				3.
		1				x4
	0										0											0
												2 2 arcsin x
5.	13					dx			;	6.											dx; 7.	2	x cos xdx;
				4
																			2
						3	x				12					1 x						0
	2

	16		dx
4.							;
	0		x 9		x

1

2 e x dx

8. x2 ;

1

	9	x		1			e		dx			3		xdx			e	1
9.						dx; 10.					; 11.					;	12.	ln x 1 dx;
														sin 2
	4		x	1			1	x 1 ln 2 x							x			0
												4

Питання для самоконтролю

1.Що називається визначеним інтегралом?

2.Записати формулу Ньютона-Лейбніця.

3.У чому полягає геометричний зміст визначеного інтегралу?

4.Сформулювати теорему про існування визначеного інтеграла.

5.Сформулювати та довести властивості збереження знака визначеного інтеграла.

6.Сформулювати та геометрично проілюструвати теорему про оцінку інтеграла.

7.Сформулювати та геометрично проілюструвати теорему про середнє значення.

8.Сформулювати теорему про похідну від інтеграла зі змінною верхньою

межею.

9.У чому полягає метод інтегрування частинами у визначеному інтегралі.

10.У чому полягає метод заміни змінної у визначеному інтегралі?

Тема 12. Інтегральне числення

Мета заняття. Вивчення теми надасть студентам можливість знати поняття

невласних інтегралів, дослідження невласних інтегралів на збіжність та вивчити

подвійні інтеграли.

План заняття

1.Невласні інтеграли від функцій, визначених на нескінченному проміжку

(невласні інтеграли першого роду).

2.Невласні інтеграли другого роду.

3.Подвійні інтеграли.

Методичні рекомендації до практичного заняття

Невласні інтеграли першого роду

Нехай функція f(x) визначена і неперервна на інтервалі [a; ) . Тоді вона неперервна на будь-якому відрізку [a,b] .

b

Означення. Якщо існує скінчена границя lim f (x)dx , то ця границя називається

b

		a
невласним інтегралом від функції f(x) на інтервалі [a;			) .
b
Позначається: lim f (x)dx	f (x)dx .
b
a	a
Якщо ця границя існує і скінчена, то кажуть, що невласний інтеграл є збіжним.
Якщо границя не існує або нескінченна, то невласний інтеграл є розбіжним.
Аналогічно визначають	невласні	інтеграли	на проміжках ( , a], ( , ) .
Наведемо формули, які вважатимемо робочими для обчислення:
	b	b
	f (x)dx	lim f (x)dx
		a
		a

c

f (x)dx

f (x)dx

f (x)dx .

c

Ознаки порівняння

Теорема. Якщо для всіх х (x

a) виконується умова 0

f (x)

(x) і інтеграл

(x)dx збігається, то

f (x)dx також збігається і

a

a

(x)dx

f (x)dx .

a

a

Теорема. Якщо для всіх х (x a)

виконується умова

0

(x) f (x)

і інтеграл

(x)dx розбіжний, то

f (x)dx також розбіжний.

a

a

Теорема. Якщо

f (x)

dx збігається, то збігається і інтеграл

a

f (x)dx .

a

В цьому випадку інтеграл

f (x)dx називається абсолютно збіжним.

a

Невласні інтеграли другого роду

Означення. Якщо функція

f (x)

необмежена в будь-якому околі точки c

відрізка [a,b] і неперервна при a

x

c і c

x

b , то

b

c

b

f (x)dx lim

f (x)dx

lim f (x)dx .

0

0

a

a

c

Якщо границі

в правій частині

рівності

існують і

скінченні, то

невласний

інтеграл називається збіжним, в протилежному випадку – розбіжним. У випадку

c a або c	b означення відповідним чином спрощується.
		Подвійні інтеграли
Нехай у замкненій обмеженій області D площини xOy визначено неперервну
функцію z	f (x, y) .	Розіб‟ємо область D довільним чином	на	n областей Di	із
площами	S1 , S2 ,...,	Sn . У кожній i -й елементарній області	Si	виберемо довільну
точку M i (xi , yi ) , помножимо значення функції в цій точці			f (xi , yi ) на площу		Si

n

відповідної

області

і утворимо суму

цих

добутків

f (xi , yi )

Si , яка

називається

i 1

інтегральною сумою функції f (x, y)

в області D .

Означення. Подвійним інтегралом функції

f (x, y)

за областю

D називається

границя цієї функції

n

lim

f (xi , yi )

Si

f (x, y)dS ,

0 i 1

D

де

- найбільший із діаметрів елементарних областей

Si .

Функція

z

f (x, y) ,

для

якої ця границя існує і скінчена, називається інтегрованою в цій області.

У прямокутній системі координат диференціал площі

S

dxdy,

тоді подвійний

інтеграл набере вигляду:

I

f (x, y)dxdy.

D

Якщо область D , в якій розглядається подвійний інтеграл, є прямокутником з

паралельними координатним осям сторонами, які задано рівняннями x

a , x b , y

c

, y

d ( a x

b , c x

d ), то подвійний інтеграл обчислюється за однією із формул:

b

d

f (x, y)dxdy

dx

f (x, y)dy

D

a

c

або

d

b

f (x, y)dxdy

dy

f (x, y)dx .

D

c

a

Інтеграли у правих частинах цих формул називаються повторними.

Приклади

1. Обчислити визначені інтеграли:

dx

b

dx

а)

lim

lim arctgx

b

2

1 1 x

1 1

x

b

1

b

= lim arctgb

arctg1

;

2

4 4

b

b

b

б)

ex dx

lim

ex dx lim ex

lim eb e0

0

b

0

b

0

b

0	0		sin 5x
в) cos5xdx lim		cos5xdx lim
			5
a	a	a

0

a

1	lim sin 0 sin5a	1	lim sin5a
5 a		5 a

Оскільки ця границя не існує при a , то цей інтеграл розбіжний.

2. Обчислити інтеграл або довести його розбіжність.

1 dx			lim	1 dx			lim	1
	x	2		b x		2		x
			b				b

1		1
	lim 1		1	- інтеграл збіжний.
b		b
	b

3. Змінити порядок інтегрування у повторному інтегралі

1	e y
I	dy f (x, y)dx.
0	0

Тут потрібно перейти від повторного інтеграла виду:

	d	2 ( y)
f (x, y)dxdy	dy	f (x, y)dx
D	c	2 ( y)
до інтеграла виду:
	b	2 ( x)
f (x, y)dxdy	dy	f (x, y)dx .
D	a	2 ( x)

Область інтегрування D обмежена лініями: y 0, x 0, x e y або y ln x

Якщо внутрішнє інтегрування провести по у, а зовнішнє – по х, то задану область D треба розглядати як правильну в напрямі осі OY . Оскільки лінія, на якій містяться точки входу в область, задана двома різними рівняннями, то дану область треба розробити на дві частини D1 i D2 . Маємо

D1	0	y	1, 0	x	1 ;
D2	ln x	y	1,1	x	e ;

1	e	e	1
I	dy f (x, y)dy		dx f (x, y)dy .
0	0	1	ln x

Завдання

1.

Обчислити інтеграли або довести їх розбіжність:

2

3

xdx

а)

xe x 2 dx ; б)

dx

; в)

dx

; г)

dx

; д)

0

1 x2

x 1

1 x 1 2

2 x ln x

x 2 1 2

2. Змінити порядок інтегрування:

y3

0

x

1

2

2 y

1

2 x 2

а) dx f x, y dy ; б) dy f x, y dx

dy f x, y dx.; в) dx

f x, y dy.

1

x 2

0

0

1

0..

0

x

Питання для самоконтролю

1.Що називається невласним інтегралом першого роду?

2.Що називається невласним інтегралом другого роду?

3.Яке значення називають подвійним інтегралом?

4.У чому полягає геометричний зміст подвійного інтеграла?

5.Поняття повторного інтегралу.

6.Зв'язок між подвійним та повторним інтегралами.

Тема 13. Економічна динаміка та її моделювання: диференціальні та

різницеві рівняння

Мета заняття. Вивчення теми надасть студентам можливість вивчити види

диференціальних рівнянь та методи їх розв‟язання.

План заняття

1.Звичайні диференціальні рівняння.

2.Загальний розв‟язок диференціального рівняння та його властивості.

3.Диференціальні рівняння першого порядку.

4.Диференціальні рівняння з відокремлюваними змінними.

5.Лінійні диференціальні рівняння першого порядку.

Методичні рекомендації до практичного заняття

Звичайні диференціальні рівняння

Розв'язок різноманітних геометричних, фізичних а також економічних задач часто зводяться до рівнянь, які пов‟язують незалежні змінні, які характеризують ту чи іншу задачу, з деякою функцією цих змінних і похідними цієї функції різних порядків.

Означення. Диференціальним рівнянням називається рівняння, яке пов‟язує незалежні змінні, їх функції і похідні (або диференціали) цієї функції.

Означення. Якщо диференціальне рівняння має одну незалежну змінну, то воно називається звичайним диференціальним рівнянням, якщо ж незалежних змінних дві або більше, то таке диференціальне рівняння називається диференціальним рівнянням в частинних похідних.

Означення. Найвищій порядок похідних, які входять в рівняння, називається

порядком диференціального рівняння.

Наприклад.

	x3 y		8 y x 5 0 - звичайне диференціальне рівняння 1–го порядку. В
	загальному вигляді записується F(x, y, y ) 0 .
	x	d 2 y	xy	dy	x2	y - звичайне диференціальне рівняння 2–го порядку. В
		dx2		dx

загальному вигляді записується F(x, y, y , y) 0

Означення. Загальним розв’язком диференціального рівняння називається така диференційована функція y= (x, C), яка при підстановці в початкове рівняння замість невідомої функції обертає рівняння в тотожність.

Властивості загального розв‟язку

1)Так як постійна С – довільна величина, то взагалі кажучи диференціальне рівняння має нескінченну множину розв‟язків.

2)За деяких початкових умов х=х0, у(х0)=у0 існує таке значення С=С0, при якому розв‟язком диференціального рівняння є функція у= (х, С0).

Означення. Розв'язок виду у= (х, С0) називається частинним розв’язком

диференціального рівняння.

Означення. Задачею Коші (Огюстен Луі Коші (1789-1857)- французький математик) називається знаходження будь-якого частинного розв‟язку диференціального рівняння виду у= (х, С0), що початковим умовам у(х0)=у0.