Математика для економістів Заоч. 2010 ч

Другий інтеграл, що входить в цю рівність, будемо інтегрувати частинами.

dv1

udu

; u1 u; du1

du;

(u 2

s)n

Позначимо:

udu

1

v1

;

(u 2

s)n

2(n

1)(u 2

s)n 1

u 2 du

u

1

du

;

(u 2 s)n

(2n

2)(u 2

s)n 1

2n

2 (u 2 s)n 1

Для початкового інтегралу отримали:

du

1

du

u

1

du

(u 2

s)n

s (u 2

s)n 1

s(2n

2)(u 2

s)n 1

s(2n 2)

(u 2

s)n 1

du

u

2n

3

du

.

(u 2

s)n

s(2n

2)(u 2

s)n 1

s(2n

2)

(u 2

s)n 1

Отримана формула називається рекурентною. Якщо застосувати її n-1 разів, то

du

отримаємо табличний інтеграл

.

u 2

s

Повернемося тепер до інтегралу від елементарного дробу виду IV в загальному випадку.

Mx

N

Mx

N

u

2ax

b; du 2adx;

dx (4a)n

dx

u b

(ax2

bx c)n

(2ax b)2

(4ac b2 ) n

x

; s 4ac b2 ;

2a

В

M (u b)

N

(4a)n

(4a)n M

udu

2aN

Mb

du

2a

du

2a

(u 2

s)n

2a 2a (u 2 s)n

2a

(u 2

s)n

отриманій рівності перший інтеграл за допомогою підстановки t=u2+s зводиться до

табличного tdtn , а до другого інтегралу застосовується розглянута вище рекурентна формула (див. приклади).

Інтегрування раціональних функцій Інтегрування раціональних дробів

Для того, щоб проінтегрувати раціональний дріб необхідно розкласти її на елементарні дроби.

	Теорема. Якщо R(x)	Q(x)	- правильний раціональний дріб, знаменник P(x)
		P(x)

якої є добутком лінійних і квадратичних множників (відмітимо, що будь-який многочлен з дійсними коефіцієнтами може бути записано в такому виді: P(x)=(x- a) …(x-b) (x2+px+q) …(x2+rx+s) ), то цей дріб може бути розкладений на елементарні за наступною схемою:

Q(x)

A1

A2

...

A

...

B1

B2

...

B

M1 x N1

P(x)

x a (x a)2

(x a)

(x b)

(x b)2

(x b)

x2

px q

де Ai, Bi,

M 2 x N2

M x N

R1 x S1

R2 x S2

R x S

...

...

...

(x2

px q)2

(x2

px q)

x2 rx s (x2

rx s)2

(x2

rx s)

Mi, Ni, Ri, Si – деякі постійні величини.

При інтегруванні раціональних дробів застосовують розклад початкового дробу на елементарні. Для знаходження величин Ai, Bi, Mi, Ni, Ri, Si застосовують так званий

метод невизначених коефіцієнтів, суть якого полягає в тому, що для того, щоб два многочлена були тотожньо рівні, необхідно і достатньо, щоб були рівні коефіцієнти при однакових степенях х.

Застосування цього методу розглянемо на конкретному прикладі:

Обчислити інтеграл:

9x3

30x2

28x

88

dx

(x2

6x

8)(x2

4)

Так як ( x 2

6x 8)(x 2

4)

(x

2)(x 4)(x 2 4) , то

9x3

30x2

28x 88

A

B

Cx D

(x

2)(x 4)(x2 4)

x 2

x

4

x2

4

Приводячи до спільного знаменника і прирівнюючи відповідні чисельники,

отримаємо:

A(x 4)(x 2			4) B(x 2)(x 2 4) (Cx	D)(x 2	6x 8) 9x3 30x 2 28x 88
( A B C)x3			( 4A 2B 6C D)x2	(4A 4B 8C 6D)x ( 16A 8B 8D)
9x3	30x2		28x 88.
A B	C	9		C 9	A B
4A 2B		6C D 30		D 30 4A 2B 54		6A 6B
4A 4B 8C 6D 28				2A 2B 4C 3D 14
16A	8B 8D 88			2A B D 11

C	9	A	B					C 9 A	B
D 24 2A 4B								D 24 2A 4B
2A 2B 36 4A 4B 72 6A 12B 14								4A 10B 50
2A B 24 2A 4B 11								4A 5B 35
C	9	A	B	C	9	A	B	A	5
D 24 2 A 4B				D 24 2A 4B				B 3
4 A 10B 50				4A	10B		50	C	1
50	10B		5B 35	B	3			D	2

Отже:

5

3

x

2

x

2

dx

dx

dx 5 ln

x

2

3ln

x

4

dx

dx

x 2

x 4

x 2

4

x 2 4

x 2

4

1

ln(x 2

arctg

x

5 ln

x

2

3ln

x

4

4)

C.

2

2

Інтегрування деяких тригонометричних функцій

Інтеграл виду

R(sin x, cos x)dx .

Тут R – деяка раціональна функція від змінних sin x і cos x .

Інтеграли

цього

виду

обчислюються

за

допомогою

підстановки t tg

x

. Ця

2

підстановка дозволяє перетворити тригонометричну функцію в раціональну.

2tg

x

1

tg

2

x

2

2t

2

1

t

2

sin x

,

cos x

;

2

x

1

t 2

2

x

1

t 2

1

tg

1

tg

2

2

Тоді

x

2arctgt;

dx

2dt

;

1

t 2

Таким чином:

R(sin x, cos x)dx

R

2t

,

1

t 2

2

dt

r(t)dt.

t 2

t 2

t 2

1

1

1

Зазначене перетворення називається універсальною тригонометричною підстановкою.

Наприклад. Обчислити інтеграл:

2dt

dx

dt

dt

1

t 2

2

2

4 sin x

3cos x

5

2t

1

t 2

8t 3 3t 2 5 5t 2

2t 2 8t 8

4

3

5

За

1

t 2

1

t 2

dt

dt

1

C

1

C.

t 2

4t 4

(t 2)2

t

2

tg

x

2

2

допомогою цієї підстановки завжди можна перевести тригонометричну функцію в раціональну і обчислити відповідний інтеграл. До недоліків можна віднести те, що при перетворенні може утворитись достатньо складна раціональна функція.

Інтегрування деяких ірраціональних функцій

Далеко не кожна ірраціональна функція може мати інтеграл, виражений елементарними функціями. Для знаходження інтеграла від ірраціональної функції слід застосовувати підстановку, яка дозволить перетворити функцію в раціональну,

інтеграл від якої може бути знайдено, як відомо, завжди.

Розглянемо деякі підстановки для інтегрування різних типів ірраціональних функцій.

Інтеграл виду

R

x, n

ax

b

dx де n- натуральне число.

cx

d

За допомогою підстановки n

ax

b

t

функція раціоналізується.

cx

d

ax b

t n ;

x

t n

b

;

dx

t n

b

dt;

cx

d

a

ct n

a

ct n

t n

t n

Тоді

R x, n

ax

b

dx

R

b

, t

b

dt

r(t)dt.

cx

d

a

ct n

a

ct n

Наприклад. Обчислити інтеграл:

dx

2dx

dx

2t 3 dt

t 2 dt

4 1

2x

t;

dt

;

2

3

2t 3

t 2

t 1

1 2x

4 1 2x

4 4

t

1 2x

2 t

t

dt

2 tdt

2

t

dt

t 2 2 1

1

dt

t 2

2t 2 ln

t

1

C

t

1

t

1

t

1

1 2x 241 2x 2 ln 41 2x 1 C.

Якщо до складу ірраціональної функції входять корені різних степенів, то в якості нової змінної доцільно взяти корені степеня, що дорівнює найменшому спільному кратному степенів корнів, що входять у вираз. Проілюструємо це на прикладі.

Наприклад. Обчислити інтеграл:

3 x 1

4 x 1

dx

12 x 1 t; x 1 t12 ;

(x

1) 1

6 x

1

dx

12t11dt;

12

t 3

dt

t 2

dt

12

t

t

dt

t 2

1

t 2

1

t 2 1

12

dt

6t 2

12t

6 ln(t 2 1)

12arctgt

C

1 t 2

12arctg12 x

1

C.

(t 4

t 3 )12t11dt

12

t 3

t 2

dt

t12 (1

t 2 )

t 2

1

1

1

dt

12 tdt 12

tdt

12 dt

t 2

1

t 2

1

66

x

1

1212 x

1 6 ln(6

x

1

1)

Інтеграли виду R x, ax2 bx c dx .

Існує декілька способів інтегрування такого роду функцій. В залежності від виду виразу, що стоїть під знаком кореня, обирають той чи інший спосіб.

Як відомо, квадратний трьохчлен шляхом виділення повного квадрату може бути зведений до вигляду:

u2 m2 .

Таким чином, інтеграл зводиться до одного з трьох видів:

1)R(u, m2 u 2 )du;

2)R(u, m2 u 2 )du;

3) R(u, u 2 m2 )du;

1 спосіб. Тригонометрична підстановка.

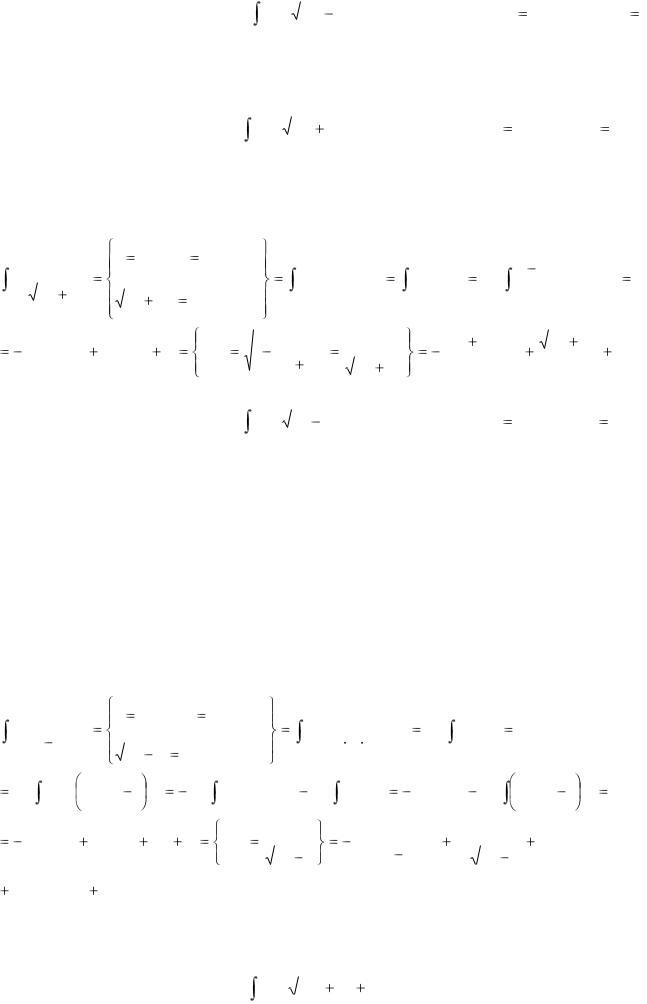
Теорема. Інтеграл виду

R(u,

m2

u 2 )du

підстановкою u

msint

або u

mcost

зводиться до інтегралу від раціональної функції відносно

sin x

або

cos x

(див.

приклади)

Теорема. Інтеграл виду

R(u,

m2

u 2 )du підстановкою u

mtgt або u

mctgt

зводиться до інтегралу від раціональної функції відносно sin x і cos x .

Наприклад.

x

atgt; dx

a

dt;

cos3 tdt

sin2 t)d sin t

dx

cos2 t

a costdt

1

(1

a

cos2 ta4tg 4ta

a 4 sin4 t

a 4

sin4 t

x 4 a 2 x 2

2

2

a

x

;

cost

1

1

C

sin t

1

a 2

x

(a 2 x 2 )3 / 2

a 2

x 2

C.

3a 4 sin3 t

a 4 sin t

a 2

x 2

a 2

x 2

3a 4 x3

a 4 x

m

m

Теорема. Інтеграл виду

R(u,

u 2

m2 )du підстановкою u

або u

sin t

cost

зводиться до інтегралу від раціональної функції відносно sint або cost .

Наприклад.

						dx							x			2			; dx			2 sin t	dt;						2 sin t costdt							1
																cost						cos2 t																				ctg 4tdt
	x(x 2					4)5 / 2																					cos2					t 2		25 tg 5t		32
															x 2	4			2tgt;
		1				ctg 2t				1					1 dt					1		ctg 2td (ctgt)						1				ctg 2tdt					1		ctg 3t					1			1				1 dt
32								sin2											32							32										96								32			sin2
													t																																					t
			1			ctg 3t					1		ctgt				t		C			ctgt		2										1										1
96										32						32																12(x 2 4)3 / 2
																									x 2	4															16			x 2		4
		1		arccos			2				C.
32							x
		2 спосіб. Підстановки Ейлера.
1) Якщо а>0, то інтеграл виду																							R(x,			ax2						bx		c )dx раціоналізується підстановкою

					ax2 bx c t		x a .
2) Якщо a<0 і c>0, то інтеграл виду							R(x, ax2 bx c )dx раціоналізується
підстановкою ax2 bx c tx c .

3) Якщо a<0 , а підкорений вираз розкладається на дійсні множники a(x–x1)(x–x2), то інтеграл виду R(x, ax2 bx c )dx раціоналізується підстановкою ax2 bx c t(x x1 )

.

3 спосіб. Метод невизначених коефіцієнтів.

Розглянемо інтеграли наступних трьох типів:

P(x)dx

dx

I.

;

II . P(x) ax2 bx cdx;

III .

;

ax2 bx

)n ax2 bx c

c

(x

де P(x) – многочлен, n – натуральне число.

Причому інтеграли II і III типів можуть бути легко зведені до виду інтегралу I

типу.

Надалі виконується наступне перетворення:

	P(x)dx						dx
			Q(x) ax2 bx c						;
	ax2 bx c						ax2 bx c

в цьому виразу Q(x) - деякий многочлен, степінь якого нижче степеня многочлена

P(x), а - деяка постійна величина.

Для знаходження невизначених коефіцієнтів многочлена Q(x), степінь якого нижче степеня многочлена P(x), диференціюють обидві частини отриманого виразу,

потім множать на ax2 bx c і, порівнюючи коефіцієнти при однакових степенях х,

визначають і коефіцієнти многочлена Q(x).

Приклади

Обчислити інтеграли: 1.

(x

2

2sin x 1)dx

x

2

dx

2

sin xdx dx

1

x

3

2cos x

x C;

3

2.

x2

sin xdx

u

x2 ; dv

sin xdx;

x2

cos x

cos x

2xdx

du

2xdx;

v

cos x

u

x; dv

cos xdx;

x2

cos x

2 x sin x

sin xdx

x2 cos x 2x sin x 2 cos x C. 3.

du

dx;

v

sin x

e2 x cos xdx

u e2 x ; du 2e2 x dx;

e2 x

sin x

sin x

2e2 x dx

dv

cos xdx; v

sin x

u e2 x ; du 2e2 x dx;

e2 x sin x 2

e2 x cos x

cos x 2e2 x dx e2 x sin x

dv

sin xdx;

v

cos x;

2e2 x cos x

4

cos xe2 x dx

5

e2 x cos xdx

e2 x (sin x 2 cos x)

e2 x

cos xdx

e2 x

(sin x

2 cos x) C.

5

4.

u

x 2 ;

dv

e5 x dx;

1

1

x 2 e5 x

2

x

2

e

5 x

dx

e

5 x

e

5 x

x

2

e

5 x

2xdx

xe

5 x

dx

du

2xdx;

v

;

5

5

5

5

5

u

x;

dv

e5 x dx;

x 2 e5 x

2 xe5 x

1

x 2 e5 x 2xe5 x

2

1

e

5 x

dx

e

5 x

dx

e5 x

du dx; v

;

5

5 5

5

5

25

25

5

x 2 e5 x

2xe5 x

2e5 x

e5 x

x 2

2x

2

.

5

25

125

5

5

25

5.

dx

dx

dx d (x 1)

d (x 1)

x 1 t

x2

2x 8

x2

2x 1 9

9 (x 1)2

dt

arcsin

t

C

arcsin

x 1

C.

32

t 2

3

3

6.

u

ln x;

dv

1

dx;

ln x

x3

ln x

1

1

ln x

1 dx

ln x

dx

dx

x3

1

1

2x 2

2x 2

x

2x 2

2 x3

2x 2

du

dx;

v

;

7.

x

2x 2

1

1

x 2

C

ln x

1

C.

2

2

2x 2

4x 2

u

ln x;

dv

xdx;

x 2

x 2

1

x 2

ln x 1

x 2

ln x x 2

x ln xdx

dx

xdx

C

1

x

2

ln x

du

dx; v

;

2

2 x

2

2

2

4

8.

x

2

x 2

(2 ln x

1)

C.

4

dx

dt

1

1

2tdt

dt

C. 9.

x

t;

2

2arctgt C

2arctg x

dx

2t

(t 2

1)t

t 2

1

(x

1) x

2

x

dx

dx

1

dx

1

arctg

x

3

C.

x2

6x 25

(x 3)2

16 16

x 3

2

16

4

1

4

10.

5x

3

dx

5x

3

dx

u

x

3; du

dx;

5u 15

3

du

5

udu

x2 6x 40

(x 3)2

x u 3;

u 2

u 2 49

49

49

11.

18

du

5

ln

u 2

49

18

ln

u

7

C

5

ln

x2

6x 40

9

ln

x

4

C.

u 2

49 2

14

u 7

2

7

x 10

3x

4

dx

3x

4

dx

u

x 3; du

x u 3;

7 x 2

6x

16 (x 3)2

udu

du

13arcsin

u

3

13

3

16 u 2

16

u 2

16 u 2

4

13arcsin

x

3

3

7

x 2

6x

C.

4

dx;	3u 9		4		du
	16		u 2

C

12.

		3x		5			dx
(x 2			4x 7)2
3			udu			11
		(u 2		3)2
3				11u
	2t			6(u 2		3)
				3
	2(x 2			4x		7)

							3x			5						dx				u	x			2;			du		dx;		3u		6	5		du
			((x					2)2		3)2										x	u			2;							(u 2		3)2
			du								t				u 2			3;			3			dt			11			u			1			du
(u 2							3)2				dt					2udu;					2			t 2				3	2(u 2 3)				3 2		u 2 3		13.
11							arctg			u					C
6			3							3
			11(x					2)								11				arctg		x		2			C.
		6(x 2						4x		7)
																6 3								3

	6x5 8x4	25x3	20x2	76x 7	dx
	3x3	4x2	17x	6

Так як дріб неправильний, то попередньо необхідно виділити цілу частину:

6x5 – 8x4 – 25x3 + 20x2 –							76x – 7	3x3 – 4x2 – 17x + 6
6x5 – 8x4 – 34x3 + 12x2								2x2 + 3
			9x3 + 8x2 – 76x - 7
			9x3 – 12x2 – 51x +18
			20x2 – 25x – 25

2x

2

3

20x2

25x 25

dx

2x

2

dx 3dx 5

4x2

5x 5

dx

2

x

3

3x

3x3 4x2

17x 6

3x3 4x2

17x 6

3

5

4x2

5x

5

dx

3x3

4x2

17x 6

Розкладемо знаменник отриманого дробу на множники. Видно, що при х = 3

знаменник дробу перетворюється в нуль. Тоді:

		3x3 – 4x2 – 17x + 6									x - 3
	3x3 – 9x2										3x2 + 5x - 2
				5x2		– 17x
				5x2		– 15x
							- 2x	+ 6
							-2x	+ 6
								0

Таким чином 3x3–4x2 –17x+6 =(x–3)(3x2 +5x–2)=(x–3)(x+2)(3x–1). Тоді:

4x 2

5x

5

A

B

C

,

(x

3)(x

2)(3x

1)

x 3

x 2

3x

1

A(x 2)(3x

1) B(x

3)(3x 1)

C(x

3)(x

2)

4x 2 5x 5 ,

Для того, щоб обійти при знаходженні невизначених коефіцієнтів розкриття дужок, групіровки і розв‟язку системи рівнянь (яка в деяких випадках може виявитись достатньо великою) застосовують так званий метод довільних значень.