Математика для економістів Заоч. 2010 ч

24.Що називається замкненою обмеженою областю?

25.Сформулювати властивості функції z = f(x, y), неперервної у замкненій обмеженій області.

26.Дати означення частинної похідної функції двох змінних по одній з них.

З‟ясувати її геометричний зміст.

27.Дати означення повного диференціала функції двох змінних та вказати формулу для його знаходження. Узагальнити цю формулу для функції n змінних.

28.Як застосовується повний диференціал функції для наближеного обчислення її значень?

Тема 10. Диференційованість функцій багатьох змінних

Мета заняття. Вивчення теми надасть студентам можливість знати методологію обчислення похідної складної та заданої неявно функції, похідної за напрямом. Також вивчити поняття градієнту функції та його властивості, поверхні та лінії рівня, зокрема, поняття лінії та поверхні байдужості в економічній теорії споживання.

План заняття

1.Похідна складної та заданої неявно функції.

2.Градієнт, властивості градієнта.

3.Похідна за напрямом.

4.Лінії рівня. Поверхні рівня.

5.Лінії та поверхні байдужості в економічній теорії.

Методичні рекомендації до практичного заняття

Похідна складної функції

1. Випадок однієї незалежної змінної. Якщо z f (x, y) є диференційованою функцією аргументів x і y , які в свою чергу є диференційованими функціями незалежної змінної t :

x	(t) , y (t) ,
то похідна складної функції z f ( (t),	(t)) може бути обчислена за формулою

dz

z dx

z

dy

.

dt

x dt

y dt

2.

Випадок багатьох незалежних змінних. Якщо z

f (x, y) є складна функція

багатьох змінних, наприклад

z

f (x, y) , де

x

(u,v) ,

y

(u, v) , де u і v - незалежні

змінні,

f , ,

- диференційовані функції,

то частинні похідні z f (x, y) по u

і v

виражаються так:

dz

z x

z

y

,

dz

z x

z

y

.

du

x

u

y u

dv

x v

y v

Диференціювання неявних функцій

Якщо рівняння f (x, y)

0 ,

де f (x, y) -

диференційована функція змінних x

і y ,

визначає y

як функцію від

x , то похідна цієї неявно заданої функції за умови, що

f y' (x, y)

0 , може бути обчислена за формулою

dy

f x' (x, y)

.

dx

f

' (x, y)

y

Частинні похідні вищих порядків

Якщо функція f (x, y) визначена в деякій області D, то її частинні похідні

f x (x, y) і f y (x, y) також будуть визначені в цій області або її частині. Будемо називати

ці похідні частинними похідними першого порядку.

Похідні цих функцій будуть частинними похідними другого порядку:

	2 z		f xx	(x, y);	2 z		f yy	(x, y);
	x2				y 2
	2 z		f xy	(x, y);	2 z		f yx (x, y);
	x y				y x

Продовжуючи диференціювати отримані рівності, отримаємо частинні похідні більш високих порядків.

Означення. Частинні похідні виду

мішаними похідними.

	2 z	;	2 z	;	3 z	;	3 z	і т.д. називаються
	x y		y x		x y x		x y y

Теорема. Якщо функція f (x, y) і її частинні похідні f x , f y , f xy , f yx визначені і

неперервні в точці М(х,у) і її околі, то вірне співвідношення:

2 f		2 f	.
x y		y x

Тобто частинні похідні вищих порядків не залежать від порядку диференціювання.

Аналогічно визначаються диференціали вищих порядків.

dz f x (x, y)dx f y (x, y)dy

d 2 z

d f

x

(x, y)dx f

y

(x, y)dy

f

x

2 (x, y)(dx)2 2 f

xy

(x, y)dxdy

f

2 (x, y)(dy)2

y

d

3 z f

x

3 (x, y)(dx)3

3 f

2

y

(x, y)(dx)2 dy 3 f

xy

2 (x, y)dx(dy)2

f

3 (x, y)(dy)3

x

y

………………….

Похідна за напрямом

Розглянемо функцію u(x, y, z)

в точці М(x,y,z) і точці М1(x+ x,y+

y, z+ z).

Проведемо через точки М і М1

вектор S . Кути нахилу цього вектора до напряму

координатних осей х, у, z

позначимо

відповідно

,

, .

Косинуси

цих кутів

називаються напрямними косинусами вектора S .

Відстань між точками М і М1 на векторі S

позначимо

S.

S

x2

y 2

z 2 .

Графічно це виглядає наступним чином:

z

M

S M1

S

y

x

Надалі припустимо, що функція u(x, y, z) неперервна і має неперервні частинні похідні по змінним х, у и z. Тоді має місце наступний вираз:

u

u

x

u

y

u

z

x 2 y

3 z ,

1

x

y

z

де величини 1, 2, 3 – нескінченно малі при

S

0 .

З геометричних міркувань очевидно:

x

cos

;

y

cos

;

z

cos

;

S

S

S

Таким чином, наведені вище рівності можуть бути записані наступним чином:

u

u

cos

u

cos

u

cos

cos

cos

cos ;

1

2

2

S

x

y

z

u

lim

u

u

cos

u

cos

u

cos

s

S

y

S 0

x

z

Відмітимо, що величина s є скалярною. Вона лише визначає напрямок вектора

S.

Зцього рівняння слідує наступне означення:

	Означення. Границя lim	u	називається похідною функції u(x,y,z) за напрямом
		S
	S 0

вектора S в точці з координатами (x,y,z). (див. приклад 1)

Градієнт

Означення. Якщо в деякій області D задана функція u=u(x,y,z) і деякий вектор,

проекції якого на координатні осі дорівнюють значенням функції u у відповідній

точці

u

;

u

;

u

, то цей вектор називається градієнтом функції u:

x

y

z

u

u

u

gradu

i

j

k .

x

dy

z

При цьому кажуть, що в області D задано поле градієнтів.

Лінії рівня

f (x, y)

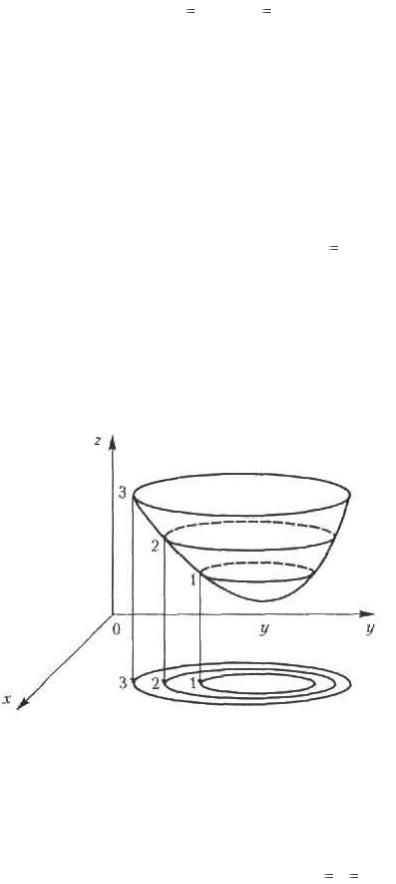
Означення. Лінією рівня функції двох змінних z називається плоска крива, яка утворюється при перетині графіка цієї функції площиною, паралельній координатній площині Oxy z C , де C const .

Лінії рівня, які відповідають різним значенням постійної величини C ,

проецируються на одну площину, наприклад, на координатну площину Oxy ; тоді їх зручно аналізувати і за їх допомогою досліджувати складний характер поверхні, що описується функцією z f (x, y) . Таким чином можна сказати, що лінії рівня функції z f (x, y) - це сім‟я кривих, які не перетинаються, на координатній площині Oxy , яка описується рівнянням виду

f (x, y) C .

Зазвичай беруть арифметичну прогресію чисел C , з постійною різницею h ; тоді за взаємним розташуванням ліній рівня можна отримати уявлення про форму поверхні, що описується функцією z f (x, y) . Там де функція змінюється швидше,

лінії рівня згущуються, а там, де поверхня рівна, лінії рівня розташовуються рідше

(див. рисунок):

Поверхні рівня

Означення. Поверхнею рівня функції u f (x, y, z) називається поверхня, на якій ця функція зберігає постійне значення

u f (x, y, z) c const .

Лінії та поверхні байдужості

Множина еквівалентних з точки зору споживача наборів благ створює поверхні байдужості. Кількість поверхонь байдужості нескінченна, - кожна людина має свої уподобання, що і відображають системи поверхонь байдужості. Окремий випадок поверхонь байдужості складають двопродуктові набори товарів. Для двопродуктових кошиків поверхні байдужості можуть бути зображені набором кривих, які називаються кривими байдужості або індиферентності.

Означення. Лінія байдужості – це лінія рівної корисності, всі точки якої показують множину наборів комбінацій двох благ, що забезпечують один і той же рівень корисності. Кожна крива відображає окремий рівень корисності.

Крива байдужості представляє функцію, яка є окремим випадком кардиналістської функції корисності, що має тільки дві змінних. Математично - це лінія рівня функції корисності. Лінією рівня функції корисності називається сукупність значень аргументів, для яких функція постійна:

TU = U(X, Y); U(X, Y) = const.

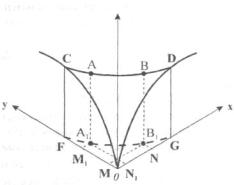
Побудуємо криву байдужості за допомогою тривимірного графіка.

На осях х та у відкладемо кількості товарів X і

Y, на осі z - сукупну корисність цих двох благ. Якби споживач мав лише одне благо

X, то сукупна корисність від його споживання зростала б по кривій 0 D , якби споживач купував лише благо Y, то сукупна корисність зростала б по кривій ОС.

Припустимо, що для кількості блага X, рівній 0G , його корисність становитиме величину DG . Така сама величина корисності для блага Y дорівнює CF для кількості

OF , отже, DG = CF . Оскільки величина корисності є однаковою, споживачу байдуже - мати 0G блага X чи OF блага У.

Так само може бути представлена множина інших комбінацій благ X і Y з

рівною корисністю, яка відповідатиме сукупній корисності кількості OF блага Y або

0G блага X. Ми одержимо ряд точок (А, В і т.д.) на кривій CD і площу корисності

CFGD для комбінацій благ ON і ОМ , ON і ОМ, і т.д. Ці комбінації благ X і Y будуть

байдужими для споживача, оскільки мають однакову корисність.

Тепер для спрощення аналізу перенесемо проекцію CD на площину Оху. Такою проекцією є пунктирна лінія FG з точками А1, В1 графіка , що відображає комбінації благ X і Y з однаковою корисністю. Це і є крива байдужості.

Рухаючись вздовж обраної кривої байдужості, споживач залишається на одному і тому ж рівні корисності, але може змінювати набір товарів у кошику.

Опуклість кривої байдужості до початку координат означає, що збільшення кількості одного товару в кошику супроводжується зменшенням кількості іншого на певну величину, тобто споживач може лише замінювати один товар іншим. Кількість одного блага, від якої споживач змушений відмовитись, щоб одержати додаткову одиницю іншого блага, називається граничною нормою заміни.

Аналіз кривих байдужості дозволяє узагальнити їх властивості:

1) Криві байдужості не можуть перетинатися, оскільки кожна крива відповідає конкретному рівню корисності. Якби криві перетиналися, це означало б,

що кошик точки перетину має не один, а декілька рівнів корисності, що суперечить припущенню щодо транзитивності уподобань споживача.

2)Криві байдужості, розташовані далі від початку координат,

відповідають наборам благ з вищим рівнем корисності, оскільки вища крива дозволяє споживачу одержувати більшу кількість обох благ порівняно з нижчою.

Споживач завжди прагне досягти найвищої з можливих кривих.

3) Криві байдужості мають від'ємний нахил, є спадними для абсолютної більшості благ. Від'ємний нахил кривої байдужості означає, що споживач повинен

відмовитись від деякої кількості одного блага, щоб мати можливість одержати додаткові одиниці іншого блага і залишитись на тому ж рівні корисності. Позитивний нахил кривої є неможливим, оскільки кошики будуть містити більшу або меншу кількість обох товарів й не належатимуть до одного набору байдужості.

4) В міру просування донизу по кривій байдужості вона стає пологішою,

випрямляється. Гранична норма заміни товару є спадною, оскільки готовність споживача до заміни товару Y товаром X зменшується з нарощуванням споживання X.

Приклади

1. Обчислити похідну функції z=x2 +y2x в точці А(1,2) за напрямом вектора АВ .

В(3, 0).

Розв'язок. Спочатку визначимо координати вектора АВ .

АВ =(3-1; 0-2) = (2; -2) = 2 i	2 j .

Визначимо модуль цього вектора:

AB = 8 22

Знаходимо частинні похідні функції z в загальному виді:

z

2x

y 2 ;

z

2 yx;

x

y

Значення цих величин в точці А :

z

6;

z

4;

x

y

Для знаходження напрямних

косинусів

вектора

АВ виконаємо наступні

перетворення:

S =

AB

2

2

i cos

j cos

i

j

AB

2

2

2

2

За величину S приймаємо довільний вектор, направлений вздовж заданого вектора,

тобто визначаючого напрямок диференціювання.

Звідси отримаємо значення напрямних косинусів вектора АВ :

								cos				=		2		;	cos	= -		2
													2						2
Отримаємо:	z		2				2					-	значення похідної заданої функції за напрямом
		6				4					2
	s		2				2
вектора АВ .
2. Знайти лінії рівня функції z														x2			y2 2x	2 y .

Розв'язок. Лінії рівня даної функції – це сім‟я кривих на площині Oxy , що описується рівнянням

x2 y2 2x 2 y C або (x 1)2 ( y 1)@ 2 C .
Остане рівняння описує сім‟ю кіл з центром в точці O1 (1,1) радіуса r	2 C .

Поверхня обертання (параболоїд), що описується заданою функцією, становиться

„крутіше” по мірі її віддалення від осі, яка визначається рівняннями x

1, y

1.

3. Знайти градієнт і його модуль функції z

xy

в точці M (0,1) .

x

y 1

Розв‟язок.

gradz

z

,

z

=

y( y 1)

,

x(x

1)

.

(x y 1)2

(x y 1)2

x y

При x

0 і y

1 отримаємо:

1,0 ,

gradz

1.

gradz

(0,1)

4. Знайти поверхні рівня функції u

x2

2x

y2

2 y

z .

Розв'язок. Відповідно означенню поверхні рівня, маємо

x2

2x y2

2 y

z

c , звідки

z (x 1)2

( y

1)2

C , де С=с+2. Отже, поверхнями рівня даної функції є параболоїди

обертання з віссю

x

1, y

1, паралельній осі Oz ,

вершини яких лежать в точках з

координатами (1,

1,

C) .

Завдання

1.

Побудувати лінії рівня функцій:

1.

z xy ;

2. z x y ;

3. z

y x2 .

2.

Знайти градієнт і його модуль для функцій в зазначених точках:

1.

z

4

x2

y2 , в точці M (1,2) ; 2. z

(x

y)2 ,

M (0,3) ; 3. u

xyz , M (3,

1,2) .

3.

Знайти частинні похідні другого порядку:

		x2		z xey , 3. z ln(x exy ) ; 4. z x2 y .
1. z			, 2.
1		2 y

Питання для самоконтролю

1.Дати означення диференційованості функції z f (x, y) .

2.Довести теорему про неперервність диференційованої функції.

3.Вивести достатні умови диференційованості функції двох змінних.

4.Що називається лінією рівня функції z f (x, y) ? Навести приклад.

5.Що називається поверхнями рівня функції u f (x, y, z) ?

Тема 11. Екстремум та умовний екстремум функції багатьох змінних

Мета заняття. Вивчення теми надасть студентам можливість набути навички дослідження функції на екстремум, знаходити найбільше та найменше значення функції в замкненій області. Вивчити поняття умовного екстремуму функції багатьох змінних і метод Лагранжа, типові оптимізаційні задачі економіки в сфері виробництва і споживання: прибуток від виробництва товарів, задача цінової дискримінації, оптимізаційний розподіл ресурсів, гранична норма заміни факторів.

План заняття

1.Екстремум функції багатьох змінних.

2.Найбільше та найменше значення функції багатьох змінних в замкненій області.

3.Умовний екстремум. Метод Лагранжа.

4.Оптимізаційні задачі економіки.

Методичні рекомендації до практичного заняття

Екстремум функції багатьох змінних

Означення. Якщо для функції z f (x, y) , визначеній в деякій області, в деякому околі точки М0(х0,у0) виконується нерівність

f (x0 , y0 ) f (x, y) ,

то точка М0 називається точкою максимуму.