Математика для економістів Заоч. 2010 ч

xOy .

Теорема Коші (теорема про існування і єдиність розв‟язку диференціального рівняння 1- го порядку). Якщо функція f(x, y) неперервна в деякій області D в

площині xOy і має в цій області неперервну частинну похідну y	f (x, y) , то якою б
не була точка (х0,у0) в області D, існує єдиний розв’язок y (x)	рівняння y f (x, y) ,

який визначений на деякому інтервалі, який містить точку х0, і приймає при х = х0

значення (х0) = у0, тобто існує єдиний розв’язок диференціального рівняння.

Означення. Інтегралом диференціального рівняння називається будь-яке рівняння, що не містить похідних, для якого дане диференціальне рівняння є наслідком.

Означення. Інтегральною кривою називається графік y= (x) розв‟язку диференціального рівняння на площині

Означення. Особовим розв’язком диференціального рівняння називається таке рішення, в усіх точках якого умова єдиності Коші не виконується, тобто в околі деякої точки (х, у) існує не менш двох інтегральних кривих.

Особові розв‟язки не залежать від постійної С.

Особові розв‟язки не можна отримати із загального розв‟язку ні за яких значеннях постійної С. Не кожне диференціальне рівняння має особові розв‟язки.

Диференціальні рівняння першого порядку.

Означення. Диференціальним рівнянням першого порядку називається співвідношення, яке пов‟язує функцію, її першу похідну і незалежну змінну, тобто співвідношення виду:

F(x, y, y ) 0

Якщо таке співвідношення привести до виду y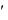f (x, y) то це диференціальне рівняння першого порядку буде називатись рівнянням, розв’язаним відносно похідної.

Перетворимо такий вираз далі:

	dy	f (x, y); dy f (x, y)dx; f (x, y)dx dy 0;
	dx

	Функцію f(x,y) запишемо у вигляді: f (x, y)	P(x, y)	, Q(x, y) 0; тоді при
		Q(x, y)
	підстановці в отримане вище рівняння маємо:
	P(x, y)dx Q(x, y)dy 0
	- диференціальна форма рівняння першого порядку.

Розглянемо типи рівнянь першого порядку і методи їх розв‟язку.

Рівняння виду y’ = f(x)

Нехай функція f(x) – визначена і неперервна на деякому інтервалі a<x<b. В

такому випадку всі

розв‟язки даного диференціального рівняння знаходяться як

y

f (x)dx

C . Якщо задані початкові умови х0 і у0, то можна визначити постійну С.

Рівняння з відокремлюваними змінними

Означення.

Диференціальне

рівняння y

f (x, y) називається рівнянням з

відокремлюваними змінними, якщо його можна записати у вигляді

y

(x) ( y) .

Таке рівняння можна зобразити також у вигляді:

y

(x) ( y)

0;

dy (x) ( y)dx

0;

dy

(x)dx 0 при ( y) 0;

( y)

Перейдемо до нових позначень

(x)

X (x);

1

Y ( y);

( y)

Отримаємо:

X (x)dx

Y( y)dy

0;

X (x)dx Y ( y)dy C .

Після знаходження відповідних інтегралів отримаємо загальний розв‟язок диференціального рівняння з відокремлюваними змінними.

Якщо задані початкові умови, то при їх підстановці в загальний розв‟язок знаходиться постійна величина С, а, відповідно, і частинний розв‟язок.

Однорідні рівняння

Означення. Функція f(x, y) називається однорідною n–го виміру відносно своїх аргументів х і у, якщо для будь-якого значення параметра t (окрім нуля) виконується тотожність:

f (tx, ty) t n f (x, y).

Означення. Диференціальне рівняння виду yf (x, y) називається однорідним,

якщо його права частина f(x,y) є однорідна функція нульового виміру відносно своїх аргументів.

Будь-яке рівняння виду P(x, y)dx Q(x, y)dy 0 є однорідним, якщо функції P(x, y)

і Q(x, y) – однорідні функції однакового виміру.

Розв'язок будь-якого однорідного рівняння оснований на зведенні цього

рівняння до рівняння з відокремлюваними змінними.

Розглянемо однорідне рівняння yf (x, y).

Так як функція f(x,y) – однорідна нульового виміру, то можна записати:

f (tx,ty) f (x, y).

	Так як параметр t довільний, припустимо, що t							1	. Отримаємо:
								x
			f (x, y)	f 1,		y
						x
	Права частина отриманої рівності залежить фактично лише від одного
	аргументу u	y	, тобто
		x
			f (x, y)	y			(u);
				x

Початкове диференціальне рівняння таким чином можна записати у вигляді: y (u)

Далі заміняємо

y = ux, y u x ux .

	u x ux	(u); u x u	(u); u	(u) u	;
				x

таким чином, отримали рівняння з відокремлюваними змінними відносно невідомої функції u :

	du		dx	;	du			dx	C .
	(u) u		x		(u)	u		x
Далі, замінивши допоміжну функцію u						на її вираз через х і у і обчисливши

інтеграли, отримаємо загальний розв‟язок однорідного диференціального рівняння.

Рівняння, які зводяться до однорідних

ax

by

c

Розглянемо рівняння виду:

y f

.

a1 x

b1 y

c1

Якщо визначник

a

b

0,

то змінні можуть бути відокремлені підстановкою

a1

b1

x u ;

y v

;

де

і

- розв‟язки системи рівнянь

ax

by

c

0 .

a1 x

b1 y

c1

0

Лінійні рівняння

Означення. Диференціальне рівняння називається лінійним відносно невідомої функції і її похідної, якщо воно може бути записано у вигляді:

y P(x) y Q(x),

при цьому, якщо права частина Q(x) дорівнює нулю, то таке рівняння називається

лінійним однорідним диференціальним рівнянням, якщо права частина Q(x) не дорівнює нулю, то таке рівняння називається лінійним неоднорідним

диференціальним рівнянням. P(x) і Q(x) - функції неперервні на деякому проміжку a<x<b.

Лінійні однорідні диференціальні рівняння Розглянемо методи знаходження загального розв‟язку лінійного однорідного

диференціального рівняння першого порядку виду

y P(x) y 0.

Для цього типу диференціальних рівнянь відокремлювання змінних не є складністю:

					dy		P(x)dx
					y
	ln	y					P(x)dx ln	C	;
		ln			y		P(x)dx;
					C
Загальний розв‟язок:	y Ce				P ( x)dx .

Лінійні неоднорідні диференціальні рівняння

Для інтегрування лінійних неоднорідних рівнянь (Q(x) 0) застосовують два

методи: метод Бернуллі і метод Лагранжа.

Метод Бернуллі

(Якоб Бернуллі (1654-1705) – швейцарський математик.)

Метод полягає в тому, що шукана функція зображується у вигляді добутку двох

	функцій y uv .
	При цьому очевидно, що y u	dv	v	du	- диференціювання частинами.
		dx		dx

Підставляючи в початкове рівняння, отримаємо:

	u		dv		v	du			P(x)uv Q(x) ,
			dx			dx
	u	dv			v		du		P(x)u Q(x) .
		dx					dx
	Так як функції u і v довільні,						то можна одну із них вибрати так, що вираз

	du	P(x)u 0 .
	dx

Таким чином, можливо отримати функцію u, проінтегрувавши, отримане співвідношення як однорідне диференціальне рівняння за описаною вище схемою:

du

P(x)dx;

du

P(x)dx;

ln

u

P(x)dx;

u

u

P( x)dx ; C 1/ C1 ;

ln

C1

ln

u

P(x)dx;

u Ce

Для знаходження другої невідомої функції v підставимо отриманий вираз для

функції u в рівняння u

dv

v

du

P(x)u Q(x)

з урахуванням того, що вираз у дужках

dx

dx

дорівнює нулю:

Сe

P( x)dx dv

Q(x);

Cdv

Q(x)e

P( x)dx

dx;

dx

Інтегруючи, можемо знайти функцію v:

Cv Q(x)e

P( x)dx

dx C1 ;

v

1

Q(x)e

P( x)dx

dx C2 ;

C

Тобто отримали другу складову добутку

y

uv . Підставляючи отриманні

значення, отримаємо:

y uv Ce

P( x)dx

1

Q(x)e

P( x)dx

dx C2 .

C

Остаточно отримаємо формулу:

y e

P( x)dx

Q(x)e P( x)dx dx

C2 , С2 – довільний коефіцієнт.

Це співвідношення може вважатися розв‟язком неоднорідного лінійного диференціального рівняння в загальному вигляді за методом Бернуллі.

Метод варіації довільної сталої Розглянемо лінійне неоднорідне диференціальне рівняння:

y P(x) y Q(x) .

Перший крок даного методу полягає у відкиданні правої частини рівняння і заміні її нулем:

y P(x) y 0

Далі знаходиться розв‟язок отриманого однорідного диференціального

рівняння:

				y	C e	P ( x)dx .
					1
Для того, щоб знайти відповідні рішення неоднорідного диференціального
рівняння, будемо вважати постійну С1					деякої функцією від х.
Тоді за правилами диференціювання добутку функцій отримаємо:
y	dy		dC1 (x)	e	P( x)dx	C1 (x)e	P( x)dx	( P(x)) .
	dx		dx

Підставимо отримане співвідношення в шукане рівняння:

dC1 (x)	e	P( x)dx	C1 (x)P(x)e	P( x)dx	P(x)C1 (x)e	P( x)dx	Q(x) ,
dx

dC1 (x) eP( x)dx Q(x);

dx

З цього рівняння визначимо змінну функцію С1(х):

dC1 (x) Q(x)e P ( x)dx dx;

Інтегруючи, отримаємо:

C1 Q(x)eP( x)dx dx C .

Підставляючи це значення в початкове рівняння, отримаємо:

y e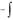P( x)dx Q(x)eP( x)dx dx C .

Таким чином, ми отримали результат, повністю співпадаючий з результатом розрахунку по методу Бернуллі.

Рівняння Бернуллі

Означення. Рівнянням Бернуллі називається рівняння виду

y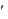 Py Q y n ,

де P і Q – функції від х або постійні числа, а n – постійне число, яке не дорівнює

1.

F(x, y).

	Для розв‟язку рівняння Бернуллі застосовують підстановку z	1	, за
		y n 1

допомогою якої, рівняння Бернуллі зводиться до лінійного.

Для цього розділимо початкове рівняння на yn.

	y	P	1	Q;
	y n		y n 1

Примінимо підстановку, враховуючи, що

z	(n 1) y n 2				y		(n 1) y	.
	y 2n
			2				y n
			z		Pz	Q
		n	1

z (n 1)Pz (n 1)Q

Тобто отримали лінійне рівняння відносно невідомої функції z.

Розв'язок цього рівняння будемо шукати у вигляді:

z e	Pdx	P dx	dx C
		Q e 1
		1

Q	(n 1)Q;	P (n 1)P.
1		1
Рівняння в повних диференціалах

Означення. Диференціальне рівняння першого порядку виду:

M (x, y)dx N(x, y)dy 0

називається рівнянням в повних диференціалах, якщо ліва частина цього рівняння являє собою повний диференціал деякої функції u

Інтегрування такого рівняння зводиться до знаходження функції u, після чого розв‟язок легко знаходиться у вигляді: du 0; u C.

Таким чином, для розв‟язку потрібно визначити:

1)в якому випадку ліва частина рівняння являє собою повний диференціал функції u;

2)як знайти цю функцію.

Якщо диференціальна форма M (x, y)dx N(x, y)dy є повним диференціалом

деякої функції u, то можна записати:

du M (x, y)dx N(x, y)dy	u	dx	u	dy.
	x		y

		u	M (x, y)
		x
	Тобто		.
		u
			N (x, y)
		y

Знайдемо мішані похідні другого порядку, продиференціювавши перше рівняння по

у, а друге – по х:

2u			M (x, y)
x	y		y
2u			N (x, y)
x	y		x

Прирівнюючи ліві частини рівнянь, отримаємо необхідну і достатню умову

того, що ліва частина диференціального рівняння є повним диференціалом. Ця умова також називається умовою тотальності:

M (x, y)		N (x, y)	.
y		x

Тепер розглянемо питання про відшукання функції u.

	Проінтегрувавши рівність	u	M (x, y) :
		x

u M (x, y)dx C( y).

Після інтегрування отримаємо не постійну величину С, а деяку функцію С(у),

так як при інтегруванні змінна у вважається постійним параметром.

Визначимо функцію С(у).

Продиференцюємо отриману рівність по у.

u	N(x, y)		M (x, y)dx C ( y).
y		y

Звідки отримаємо: C ( y) N(x, y)		M (x, y)dx.
	y

Для знаходження функції С(у) необхідно проінтегрувати наведене вище рівняння.

Визначимо функцію С(у):

C( y)	N (x, y)		M (x, y)dx dy C
		y

Підставляючи цей результат у вираз для функції u, отримаємо:

u M (x, y)dx N (x, y)		M (x, y)dx dy C.
	y

Тоді загальний інтеграл початкового диференціального рівняння буде мати вигляд:

M (x, y)dx N (x, y) y M (x, y)dx dy C.

Приклади

1. Знайти загальний розв‟язок диференціального рівняння xy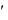 y 0.

Розв'язок. Загальний розв‟язок диференціального рівняння знаходиться за допомогою інтегрування лівої і правої частин рівняння, яке попередньо перетворимо наступним чином:

x dydx y 0 xdy ydx

dy dx

y x

Тепер інтегруємо:	dy		dx
	y		x

ln y	ln x	C0
ln y ln x		C0
ln xy	C0

xy eC0 C

yCx - це загальний розв‟язок заданого диференціального рівняння.

2.Знайти загальний розв‟язок диференціального рівняння: y y 0. Знайти особливий розв‟язок, якщо він існує.

		dy			y
		dx
	dy			dx
		y
	dy				dx
		y
ln y				x	C
y				e x	eC

y C1 e x

Дане диференціальне рівняння має також особливий розв‟язок у=0. Цей розв‟язок неможливо отримати із загального, однак при підстановці в задане рівняння отримаємо тотожність.

	3. Знайти загальний розв‟язок диференціального рівняння:				yy	2x
						cos y
	Розв'язок.	y cos y	dy	2x
			dx

y cos ydy 2xdx

y cos ydy 2xdx

Інтеграл, що стоїть в лівій частині, інтегрується частинами:

	y cos ydy	u	y; dv	cos ydy;		y sin y	sin ydy y sin y cos y
		du	dy; v	sin y
			y sin y		cos y	x 2	C
			y sin y		cos y	x 2 C	0

- це і є загальний інтеграл даного диференціального рівняння, так як шукана функція і не виражена через незалежну змінну. В цьому і полягає відмінність загального

(частинного) інтеграла від загального (частинного) розв’язку.

	3. Знайти розв‟язок диференціального рівняння				y	ln y за умови у(2) = 1.
					y
	Розв'язок.	ydx		ln y
		dy

dx	ln ydy
		y
dx		ln ydy
		y
x C	ln yd(ln y)

x C	ln2	y
	2

за умови у(2) = 1 отримаємо 2 C					ln2 1			;	2 C 0;	C 2;
						2
Отже: 2(x 2) ln2 y; або y e		2 x 4		- частинний розв‟язок.
4. Розв‟язати рівняння	y			y 2 3 .
Розв'язок.	dy			y	2	3
	dx