11.2.1. Функции расстояния

Для решения задачи кластерного анализа необходимо количественно определить понятия сходства и разнородности. Для этого вводится понятие расстояния (отдаленности) между соответствующими точками x_i и x_j. Если это расстояние достаточно мало, объекты i и j попадают в один кластер, если оно велико – в разные.

Используются следующие наиболее употребимые меры расстояния:

Евклидово расстояние: d₂(X_i, X_j) =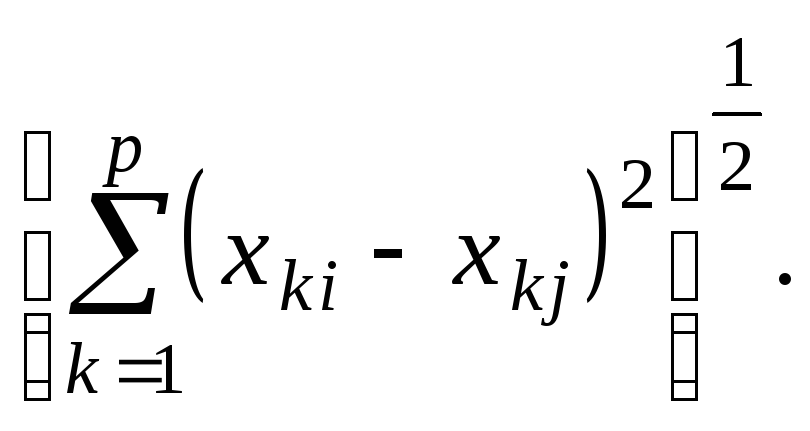(11.2)

l₁ - норма: d₁(X_i , X_j) =(11.3)

l_р - норма: d_p(X_i, X_j) =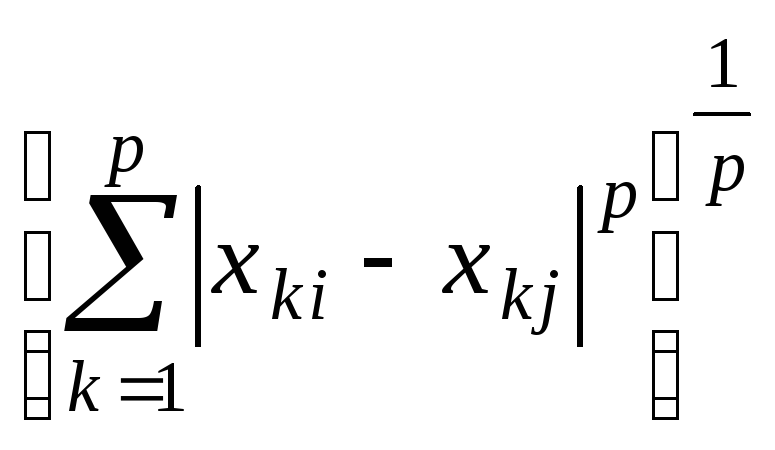(11.4)

Мера Джеффриса-Матуситы: M=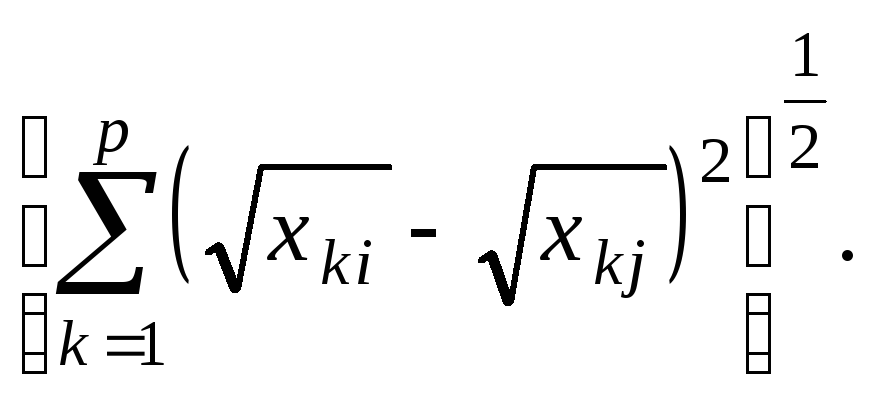 (11.5)

Коэффициент дивергенции Кларка: СD =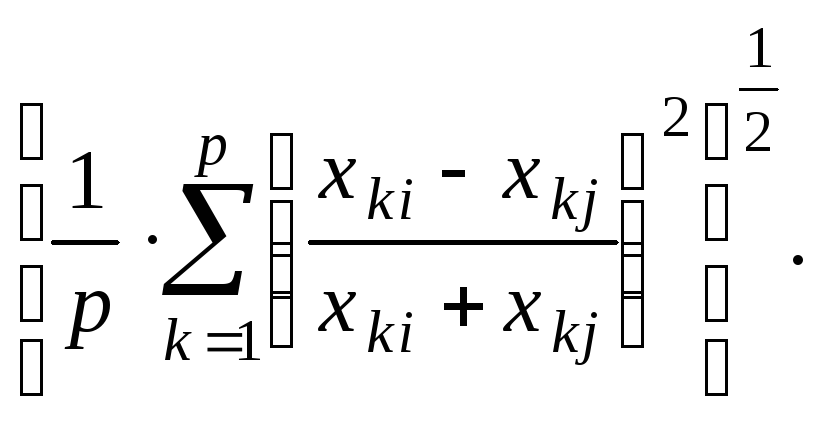(11.6)

Существуют и другие, более сложные меры расстояния, выбор которых определяется как субъективным предпочтением исследователя, так и естественным стремлением к упрощению процедуры эксперимента.

11.2.2. Меры сходства

Как правило, в качестве меры сходства используется корреляция между рядами признаков (переменных). Объекты (признаки) считаются сходными, если коэффициент корреляции близок к +1 (положительное сходство) или к –1 (отрицательное сходство), и не сходны, если r_ij близок к нулю. В качестве граничного значения для объединения переменных в один кластер используется критическое значение коэффициента корреляции, которое находится по соответствующим таблицам.

При построении векторных моделей необходимо подчеркнуть следующее: если X_i и X_j рассматривать как координаты двух точек в многомерном пространстве, то r_ij = cos q, где q - угол между двумя векторами.

11.2.3. Выбор числа кластеров

Кластеризация полным перебором

Является наиболее прямым способом решения проблемы и заключается в полном переборе всех возможных разбиений на кластеры и отыскании такого разбиения, которое ведет к оптимальному (минимальному) значению целевой функции. Такая процедура выполнима лишь в тех случаях, когда n (число объектов) и m (число кластеров) невелико, поскольку число разбиений (W) прогрессивно возрастает с увеличением n и m (напомним, что n ³ m). Число возможных разбиений при ограниченном числе объектов и кластеров приведено в табл. 11.1.

Таблица 11.1

	n = 4	n = 5	n = 6	n = 7	n = 8
m =1	1	1	1	1	1
m =2	7	15	31	63	127
m =3	6	25	90	301	966
m =4	1	10	65	350	1701

Динамическое программирование

Суть методов динамического программирования состоит в целенаправленном поиске разбиения, дающего минимальное значение величины W. При этом все разбиения, которые приводят к большему значению W, отбрасываются.

Пример:

При n = 6 и m = 3, W = 90. При этом 90 альтернатив кластеризации дают 3 формы распределения:

1: {4}, {1}, {1} – 15 возможных вариантов;

2: {3}, {2}, {1} – 60 " "

3: {2}, {2}, {2} – 15 " "

Оптимальное распределение соответствует форме 3, которая и служит основой для дальнейшего перебора вариантов:

(1, 2) (3, 4) (5, 6)

(1, 3) (2, 4) (5, 6)

(1, 4) (2, 3) (5, 6) и т. д.

В процедуре динамического программирования имеются повторения сочетаний признаков в одном и том же кластере (в нашем примере (5, 6)), что в значительной мере сокращает число вычислений.

Естественно, что такой подход несколько произволен, так как минимизация числа разбиений, по сути, не означает, что именно эти распределения являются оптимальными.