9.5.2. Свойства сильно вогнутых (выпуклых) функций

Теорема 9.13. Сильно вогнутая (выпуклая) функция является строго вогнутой (выпуклой) функцией.

Теорема 9.14. Сумма сильно вогнутой (выпуклой) и вогнутой (выпуклой) функций на выпуклом множестве будет сильно вогнутой (выпуклой) на с той же константой .

Теорема 9.15. Если сильно вогнута (выпукла) на с константой , то при любом будет сильно вогнутой (выпуклой) на с константой .

Теорема 9.16. Пусть функция непрерывна и сильно вогнута (выпукла) на выпуклом множестве , тогда ограничена сверху на этом множестве.

Доказательство. Если множество ограничено, то утверждение теоремы следует из теоремы Вейерштрасса.

Пусть – неограниченное замкнутое выпуклое множество. Возьмем произвольную точку . В силу непрерывности на для любого существует такое число , что имеет место неравенство

для всех (9.15.)

откуда для всех .

Пусть , то есть .

Тогда число . (*)

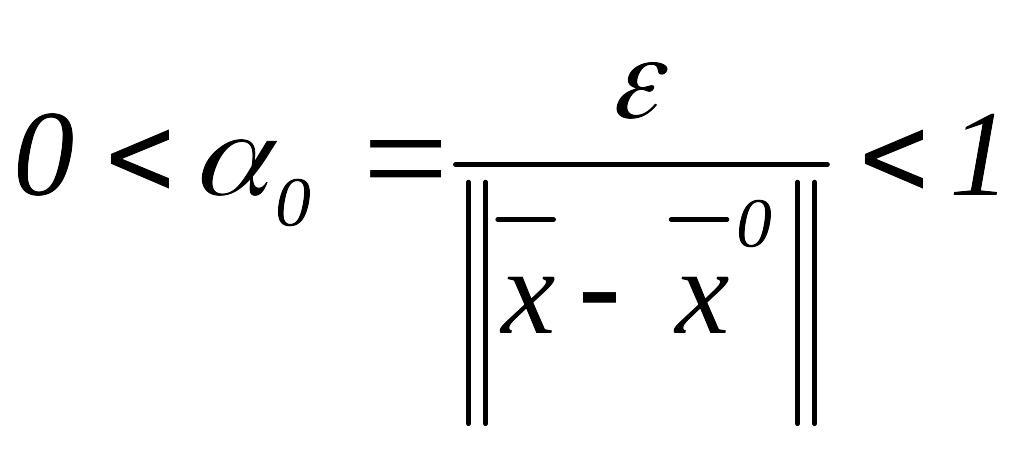Из определения сильной вогнутости при , имеем

(9.16.)

Положим, , тогда , т.е. точка , и из (1.3.2) следует, что , (9.17.)

Тогда из (9.16.) с учетом (9.17.) получим или

(9.18.)

Преобразуем неравенство (9.18.) с учетом (*)

(9.19.)

Применяя к последнему слагаемому (9.19.) неравенство будем иметь

(9.20.)

для всех .

С учетом (*) получим

(9.21.)

для всех .

Таким образом, из неравенств (9.15.) и (9.21.) следует, что функция ограничена сверху на множестве .

Теорема 9.16. Пусть функция непрерывна и сильно вогнута на выпуклом множестве , тогда , если .

Доказательство. Утверждение теоремы следует из неравенства (9.20.).

Теорема 9.17. Если функция непрерывна и сильно вогнута на выпуклом замкнутом множестве , то множество выпукло, замкнуто и ограничено для любого .

Доказательство. Рассмотрим множество , где

а) Выпуклость множества следует из теоремы 18.

б) Замкнутость следует из непрерывности функции на .

в) Множество ограничено.

Предположим, что это не так, тогда найдется последовательность такая, что при . Но тогда в силу теоремы 9.16 найдется такое , что для всех , и, следовательно, при , т.е. предположение о неограниченности является неверным.

9.5.3. Критерии сильной вогнутости (выпуклости)

Теорема 9.18. Пусть – выпуклое множество, функция . Тогда для того, чтобы была сильно вогнутой (выпуклой) на , необходимо и достаточно существование постоянной , такой, что

(9.22)

Доказательство. Необходимость. Пусть функция сильно вогнута на , тогда по определению существует постоянная , такая что

(9.23)

для любых и любого .

Преобразуем неравенство (9.23) к виду , (9.24)

Деля обе части неравенства (9.24) на и переходя к пределу при , получим (9.22):

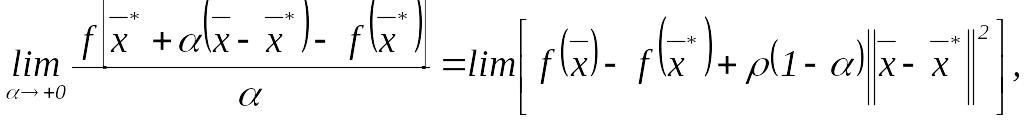или ,

где ,

или .

Достаточность. Пусть при некотором неравенство (9.22) выполнено при всех . В частности оно выполняется для точек , и , , где , , т.е. имеем

, (9.25)

(9.26)

Умножим (9.25.) на , (9.26.) – на (1- ) и сложим, в результате чего получим неравенство (1.3.10).

Теорема 9.19. Пусть – выпуклое множество, функция . Для того чтобы была сильно вогнутой (выпуклой) на , необходимо и достаточно существование постоянной , что

. (9.27)