2. Метод Ньютона

Рассмотрим разложение в ряд Тейлора в окрестностях точки :

(12.6)

Отбрасывая члены третьего порядка и выше, полагаем квадратичную аппроксимацию функции в точке :

, (12.7)

где – матрица Гессе в точке .

В качестве новой точки будем брать точку минимума квадратичной функции . Необходимым условием минимума квадратичной функции является равенство или . (12.8)

Предполагая, что матрица, обратная к , существует, получаем

или . (12.9)

Равенство (12.9) дает рекуррентную формулу для точек, генерируемых методом Ньютона. Таким образом, в методе Ньютона направление поиска задается формулой

(12.10)

т.е. направление, равное градиенту и используемое в качестве направления поиска в методе Коши, отклоняется посредством умножения на матрицу .

Пример 12.6. Найти минимум функции методом Ньютона: .

Выберем начальную точку . Тогда Так как , то , , то .

Очевидно, что оптимум квадратичной функции Ньютона находится за одну итерацию независимо от выбора начальной точки. При оптимизации неквадратичных функций метод Ньютона не является конечным. Сходимость метода Ньютона при оптимизации неквадратичных функций существенно зависит от выбора начальной точки , и теорема сходимости доказывается в предположении, что итерационный процесс начинается из точки, достаточно близкой к оптимальной. Кроме того, в методе Ньютона не гарантируется убывание функции на каждой итерации.

3. Модифицированный метод Ньютона

Метод Ньютона можно модифицировать с целью обеспечения убывания функции на каждой итерации путем осуществления одномерной оптимизации вдоль направления.

Алгоритм модифицированного метода Ньютона

Начальный этап. Выбрать – начальную точку и – параметр окончания счета, положить .

Основной этап.

1. Если , то , остановится.

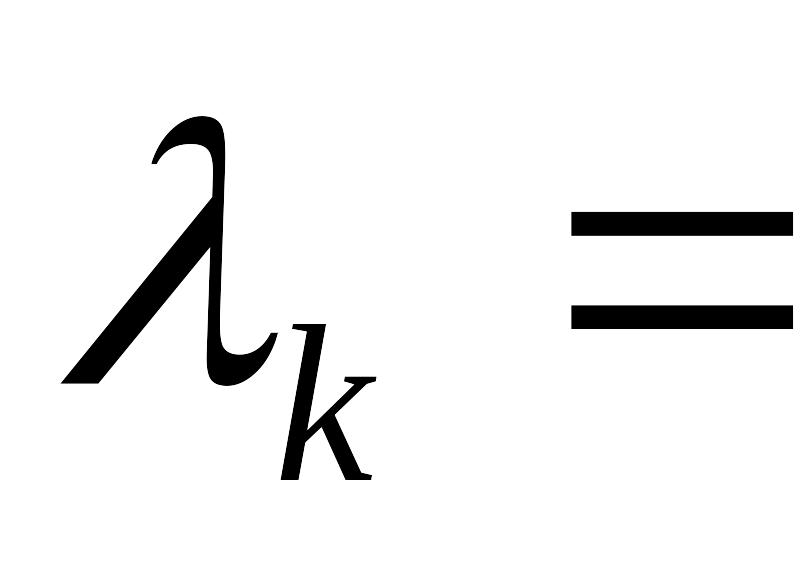
2. Положить , вычислить , , положить 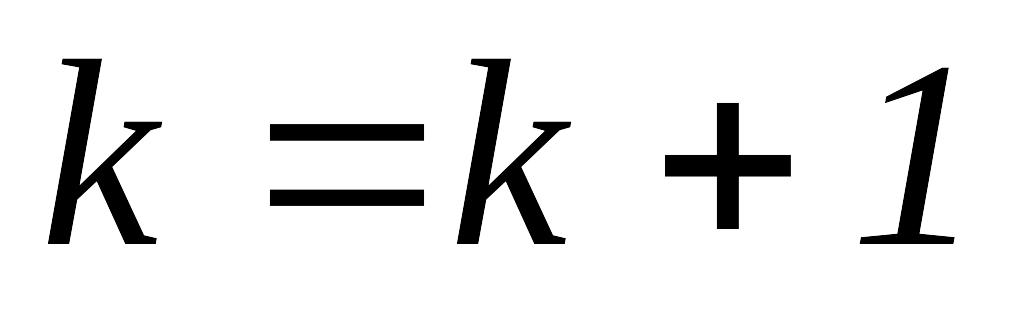и перейти к шагу 1.

Существенным недостатком метода Ньютона и его модификации является необходимость вычисления на каждой итерации матрицы и обратной к ней матрицы , что существенно увеличивает трудоемкость каждой итерации. Именно в силу этих соображений возникает необходимость создания методов, менее трудоемких, использующих значения только первых производных, но обладающих скоростью сходимости, близкой к скорости метода Ньютона. Так возникли методы квазиньютоновского типа, в которых в качестве направления спуска выбирается либо вектор , либо , где – подходящая матрица, – подходящий вектор, причем матрицы и векторы выбираются так, чтобы последовательные приближения оптимизировали квадратичную функцию за конечное число шагов.

2. Методы, использующие сопряженные направления

В данном разделе рассматриваются алгоритмы безусловной оптимизации, использующие сопряженные направления. Понятие сопряженности является очень важным при решении задач безусловной оптимизации, особенно для задач оптимизации квадратичных функций.