
- •Глава 6. Постановки задачи нелинейного программирования (знп) и основные определения…………………………...3
- •Глава 7. Задача одномерной оптимизации…………………………………….13
- •Глава 8. Графический метод решения знп…………………………………...33
- •Глава 10. Выпуклое программирование……………………………………....62
- •Глава 11. Квадратичное программирование…………………………………74
- •Глава 12. Задача безусловной оптимизации (збо)…………………………………………………………………..81
- •Глава 13. Задача условной оптимизации (зуо)……………………….……127
- •Глава 6.
- •6.1. Задача нелинейного программирования (знп) и ее постановки.
- •6.2. Основные определения.
- •6.3. Классификация знп.
- •6.4. Классическая оптимизация.
- •Глава 7. Методы одномерной оптимизации
- •Постановка задачи. Основные понятия
- •7.2. Поиск отрезка, содержащего точку максимума Алгоритм Свенна
- •Методы нулевого порядка.
- •Дихотомический поиск (метод деления отрезка пополам)
- •Метод золотого сечения
- •Метод дск-Пауэлла
- •7.4. Методы первого порядка.
- •Метод средней точки
- •Метод хорд (секущих)
- •Метод кубической аппроксимации
- •7.5. Методы второго порядка. Метод Ньютона-Рафсона
- •Итерация 1
- •Глава 8. Графический метод решения знп.
- •8.1. Алгоритм графического метода решения знп
- •8.2. Решение примеров.
- •Выпуклые и вогнутые функции
- •9.1. Определения
- •9.2. Свойства вогнутых (выпуклых) функций
- •9.3. Критерии вогнутости (выпуклости) гладких функций
- •9.4. Экстремальные свойства вогнутых (выпуклых) функций
- •9.5. Сильно вогнутые (выпуклые) функции
- •9.5.1. Определение. Примеры
- •9.5.2. Свойства сильно вогнутых (выпуклых) функций
- •9.5.3. Критерии сильной вогнутости (выпуклости)
- •9.5.4. Экстремальные свойства сильно вогнутых (выпуклых) функций
- •Глава 10. Выпуклое программирование
- •10.1. Постановка задачи
- •10.2. Функция Лагранжа. Седловая точка функции Лагранжа, условия ее существования Определение 10.1. Функция , (10.10)
- •10.3. Достаточные условия оптимальности
- •10.4. Условия регулярности выпуклого множества
- •10.5. Теорема Куна-Таккера. Общий случай
- •10.6. Теорема Куна-Таккера. Случай линейных ограничений
- •Глава 11. Квадратичное програмирование.
- •11.1. Постановка задачи квадратичного программирования (зкп)
- •11.2. Применение теории Куна-Таккера к решению зкп.
- •11.3. Решение задач.
- •Глава 12. Методы безусловной оптимизации
- •12.1. Постановка задачи
- •Алгоритм метода спуска
- •. Методы нулевого порядка (прямого поиска)
- •Метод Хука-Дживса
- •Алгоритм метода Хука-Дживса, использующий одномерный поиск
- •Метод покоординатного спуска
- •Первый вариант
- •Второй вариант
- •Методы первого и второго порядков
- •Градиентные методы. Метод скорейшего спуска – метод Коши
- •Метод Ньютона
- •Модифицированный метод Ньютона
- •Методы, использующие сопряженные направления
- •Определение сопряженных направлений
- •Оптимизация квадратичной функции. Конечная сходимость алгоритмов, использующих сопряженные направления
- •12.4.4. Метод Дэвидона-Флетчера-Пауэлла Шаг 1.Метод Дэвидона-Флетчера-Пауэлла (дфп) принадлежит к классу квазиньютоновских методов, в которых направление поиска задаётся в виде
- •Алгоритм метода дфп
- •Итерация 1
- •Шаг 2. Вычислим , тогда .
- •Шаг 2. Вычислим , тогда .
- •12.4.5. Метод сопряжённых градиентов Флетчера-Ривса
- •Алгоритм метода Флетчера-Ривса
- •Глава 13. Методы условной оптимизации
- •13.1. Постановка задачи. Классификация методов
- •Общая схема методов условной оптимизации
- •Шаг 2.Шаг 1. Выбрать ( -я итерация) – возможное направление подъёма функции в точке . Если такого направления нет, то - решение задачи. В противном случае перейти к шагу 2.
- •13.2. Методы возможных направлений
- •13.2.1. Метод Зойтендейка
- •Пример 13.2
- •Итерация 3
- •Шаг 4.Рисунок 13.6
- •13.2.2. Метод Топкиса-Вейнотта
- •Пример 13.3
- •Итерация 1
- •Шаг 5.Рисунок 13.7
- •Алгоритм метода Топкиса-Вейнотта
- •13.2.3. Метод Франка-Вульфа
- •Алгоритм метода Франка-Вульфа
- •Шаг 5. Находим шаг в направлении новой точки . Решение этой задачи (одномерной): .
- •Шаг 3. Так как , переходим к шагу 4.
- •Шаг 5. Решаем задачу: .
- •Литература
Глава 7. Методы одномерной оптимизации
Постановка задачи. Основные понятия
Задача оптимизации, в которой целевая функция задана функцией одной переменной, относится к наиболее простому типу оптимизационных задач. Тем не менее, анализ задач такого типа занимает центральное место в оптимизационных исследованиях как теоретической, так и практической направленности. Это связано с тем что, одномерные методы оптимизации часто используются для анализа подзадач, которые возникают при реализации итеративных процедур, ориентированных на решение многомерных задач оптимизации. Важность теоретических и прикладных оптимизационных задач с одной управляемой переменной обусловила разработку большого числа алгоритмов их решения. Классификация методов решения одномерных задач по существу основывается на различных предположениях и допущениях относительно природы и свойств функции [4].
Пусть
функция
![]() определена на
определена на
![]() .
Задачей одномерной оптимизации будем
называть задачу, в которой требуется
найти
.
Задачей одномерной оптимизации будем
называть задачу, в которой требуется
найти
![]() ,
.
(7.1)
,
.
(7.1)
Решением
или точкой максимума (минимума) этой
задачи назовем такую точку
![]() ,
что
,
что
![]() .
.
Методы одномерной оптимизации условно подразделяются на три группы.
- методы нулевого порядка, основанные лишь на вычислении значений самой функции
-методы первого порядка, использующие значения, как самой функции, так и ее первой производной
-методы второго порядка, использующие значения функции, ее первой и второй производной
В дальнейшем будем считать, что максимизируемая функция является унимодальной.
Определение
7.1. Функция
называется унимодальной на множестве
![]() ,
если существует единственная точка
,
если существует единственная точка
![]() ее
максимума на
и
ее
максимума на
и
![]() ,
если
,
если
![]() и
и
![]() ,если
,если
![]() для любых
для любых
![]() .
.
Другими словами, унимодальная функция монотонно возрастает слева от точки максимума и монотонно убывает справа от нее.
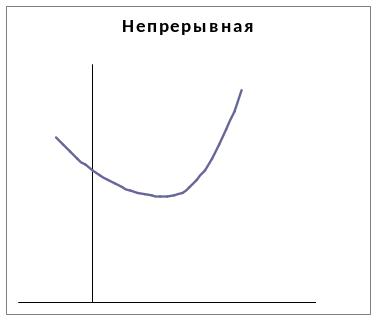
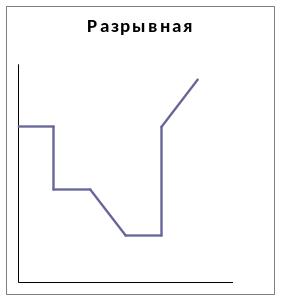
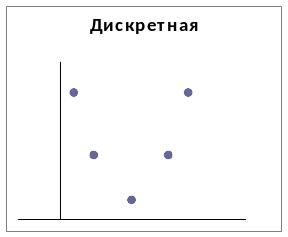
Рис. 7.1.Унимодальные функции.
Как показано на рисунке 7.1, унимодальная функция не обязательно должна быть непрерывной. Унимодальность функций является исключительно важным свойством, которое широко используется в оптимизационных исследованиях.
Фактически все одномерные методы поиска, используемые на практике, основаны на предположении, что исследуемая функция в допустимой области, по крайней мере, обладает свойством унимодальности. Полезность этого свойства определяется тем фактором, что для унимодальной функции сравнение значений в двух различных точках интервала поиска позволяет определить, в каком из заданных двумя указанными точками подынтервалов точка оптимума отсутствует [4].
Теорема 7.1.
Пусть
функция
унимодальна
на замкнутом интервале
![]() ,
а ее минимум достигается в точке
,
а ее минимум достигается в точке
![]() .
Рассмотрим точки
.
Рассмотрим точки
![]() и
и
![]() ,
расположенные в интервале таким образом,
что
,
расположенные в интервале таким образом,
что
![]() .
Сравнивая значения функции в точках
и
,
можно сделать следующие выводы:
.
Сравнивая значения функции в точках
и
,
можно сделать следующие выводы:
Если
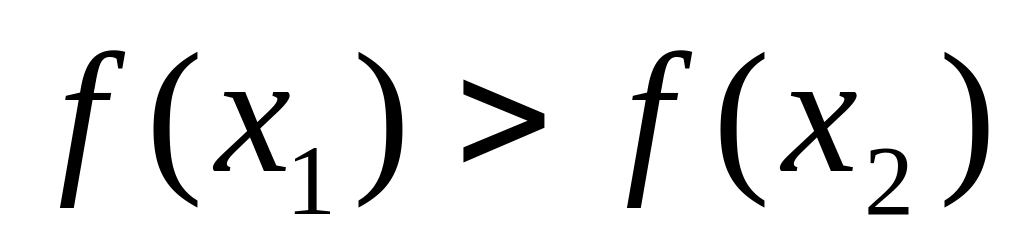 ,
то точка минимума
не лежит в интервале
,
то точка минимума
не лежит в интервале
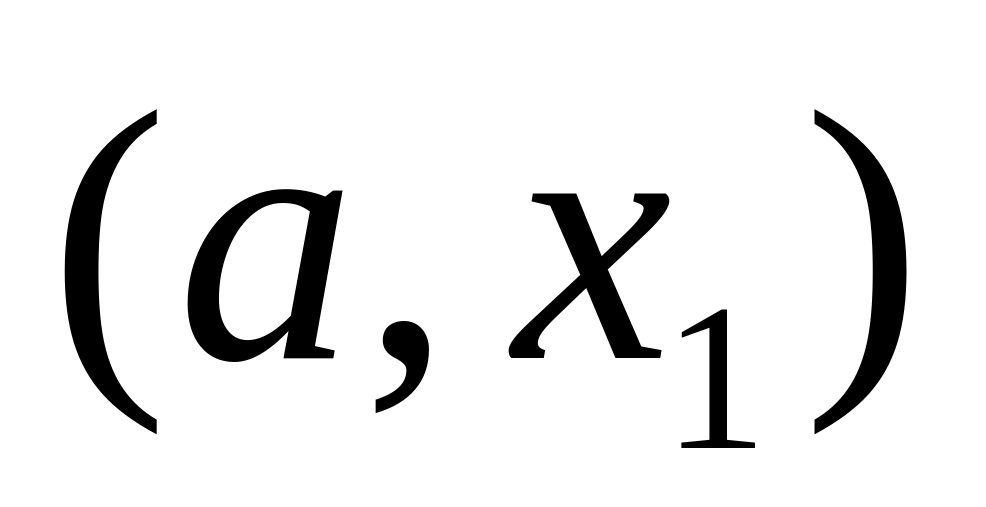 ,
т.е.
,
т.е.
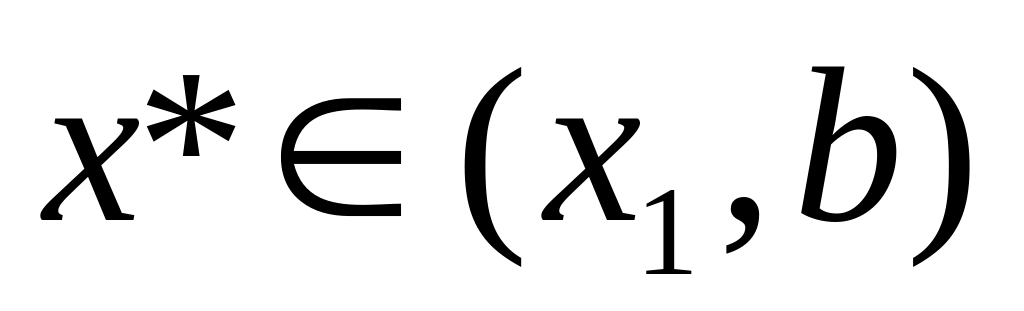
Если
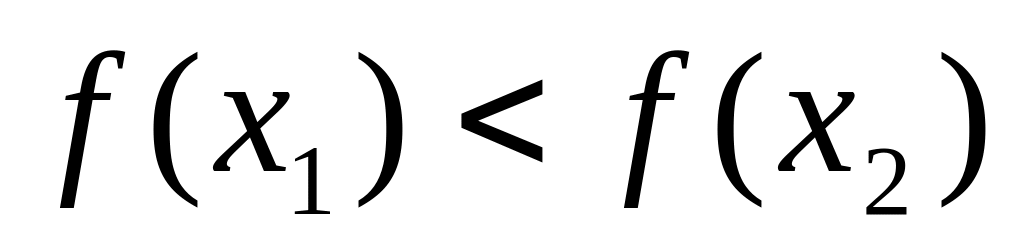 ,
то точка минимума не лежит в интервале
,
то точка минимума не лежит в интервале
 ,
т.е.
,
т.е.
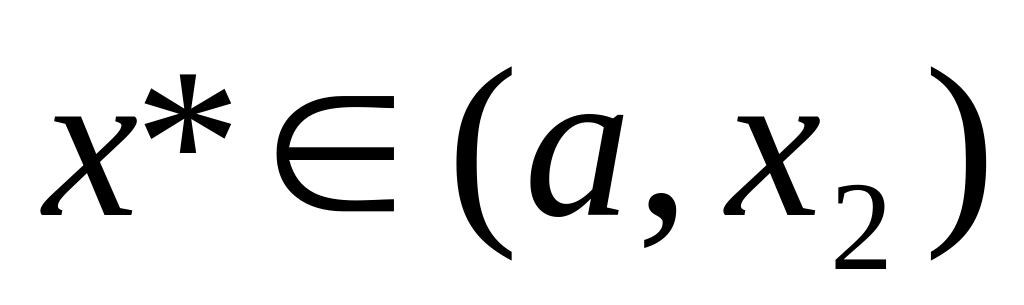
Доказательство.
Рассмотрим
случай, когда
.
Пусть утверждение теоремы неверно, т.е.
![]() .
Поскольку
.
Поскольку
![]() - точка минимума, то по определению
- точка минимума, то по определению
![]() для
всех
для
всех
![]() .
Получаем двойное неравенство:
.
Получаем двойное неравенство:
![]() при
при
![]()
Это неравенство не может выполняться, так как унимодальная функция должна быть монотонной по обе стороны от точки . Таким образом, получено противоречие, доказывающее утверждение теоремы. Аналогичные рассуждения справедливы также в случае, когда .
Примечание.
Если
![]() ,
то можно исключить оба крайних интервала
и
;
при этом точка минимума должна
располагаться в интервале
,
то можно исключить оба крайних интервала
и
;
при этом точка минимума должна
располагаться в интервале
![]() .
.
Согласно теореме, которую иногда называют правилом исключения интервалов, можно реализовать процедуру поиска, позволяющую найти точку оптимума путем последовательного исключения частей исходного ограничительного интервала. Поиск завершается, когда оставшийся подынтервал уменьшается до достаточно малых размеров. Заметим, что правило исключения интервалов, устраняет необходимость полного перебора всех допустимых точек. Несомненным достоинством поисковых методов такого рода является то, что они основаны лишь на вычислении значений функций. При этом не требуется, чтобы исследуемые функции были дифференцируемы; более того, допустимы случаи, когда функцию нельзя даже записать в аналитическом виде. Единственным требованием является возможность определения значения функции в заданных точках х с помощью прямых расчетов или имитационных экспериментов. Вообще в процессе применения рассматриваемых методов поиска можно выделить два этапа:
- этап установления границ интервала, на котором реализуется процедура поиска границ достаточно широкого интервала, содержащего точку оптимума;
- этап уменьшения интервала, на котором реализуется конечная последовательность преобразований исходного интервала с тем, чтобы уменьшить его длину до заранее установленной величины.
Отметим,
что предположение об унимодальности
функции в окрестностях точки
![]() весьма естественно, поэтому получение
информации о таком промежутке является
важным этапом процедуры оптимизации.
В разделе 7.2. данной
главы рассмотрен алгоритм первого этапа
– поиск границ отрезка, содержащего
точку максимума унимодальной функции
,
далее излагаются методы II
этапа – отыскания точки максимума на
заданном отрезке.
весьма естественно, поэтому получение
информации о таком промежутке является
важным этапом процедуры оптимизации.
В разделе 7.2. данной
главы рассмотрен алгоритм первого этапа
– поиск границ отрезка, содержащего
точку максимума унимодальной функции
,
далее излагаются методы II
этапа – отыскания точки максимума на
заданном отрезке.
