13.2.1. Метод Зойтендейка
Пусть требуется найти максимальное значение вогнутой функции :
при условиях
.
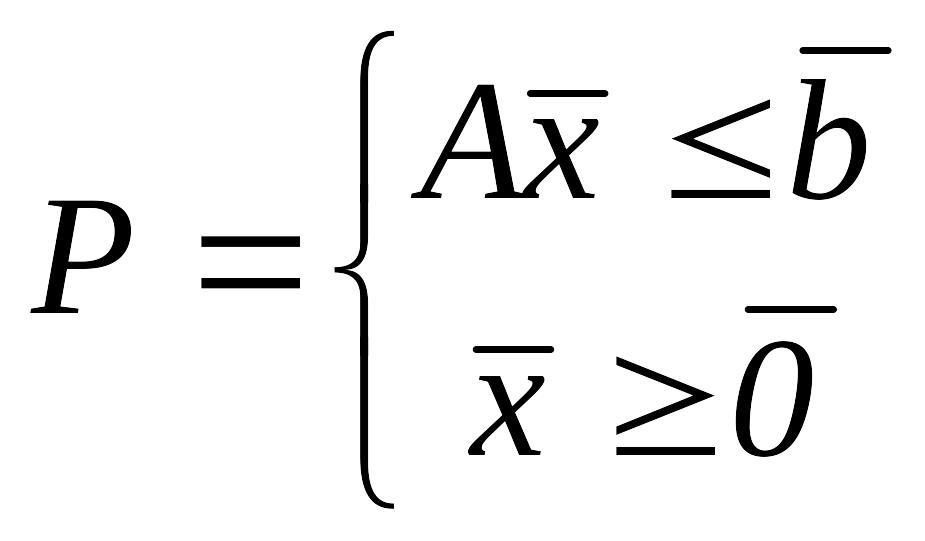(13.14)
Характерной особенностью этой задачи является то, что её система ограничений содержит только линейные неравенства.
Предположим
также для любой допустимой точки
,
что
и
,
где
и
.
Далее приводится алгоритм Зойтендейка
для случая линейных ограничений.
Алгоритм метода Зойтендейка
Начальный этап. Выбрать начальную точку , для которой
и ,
,
.
Положить .
Основной этап.
Шаг
1. Для
предполагаем, что
,
,
,
.
Шаг
2. Определить возможное направление
подъёма
,
решая следующую задачу:
(13.15)
при условиях
.
(13.16)
Шаг
3. Если
,
то
-
задача решена. В противном случае перейти
к шагу 4.
Шаг 4. Определить (шаг в направлении ), решая задачу одномерной оптимизации:
.
Шаг
5. Положить
,
заменить
на
и перейти к шагу 1.
Дадим некоторые пояснения к алгоритму.
На шаге 2 решается вспомогательная задача, являющаяся задачей линейного программирования. Конечно, надо быть уверенным в её разрешимости и, соответственно, в существовании возможного направления подъёма .
Вектор
является возможным направлением подъёма
в точке
,
если
и
.
Поскольку множество планов построенной
ЗЛП ограниченно, вспомогательная задача
всегда разрешима. А если существует
,
то
.
Причём для
:
,
следовательно,
.
Если
,
то есть возможность найти лучшую точку.
Если
,
то выбрать возможное направление подъёма
не представляется возможным.
Для
шага 4 необходимо определить величину
.
Рассмотрим неравенство:
.
Так как
,
,
то
,
.
Отсюда
и определяем
для этого неравенства.
определяется при следующих условиях:
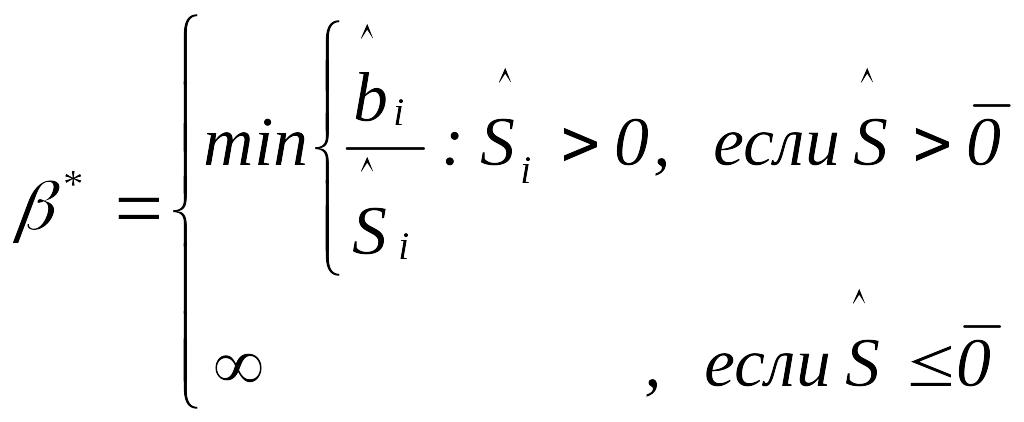(13.17)
где
,
.
Пример 13.2
.
Начальный
этап. Выбираем
начальную точку
,
для которой
,
,
,
.
.
Положить
.
Основной этап.
Итерация 1.
Шаг
1. Для
заданы
,
,
,
.
Шаг
2. 
.
Решаем задачу:
при условиях
.
При
решении этой задачи симплекс-методом
получаем
,
.
Шаг
3. Так как
,
то переходим к шагу 4.
Шаг 4. Решаем одномерную задачу:
.
Определяем (согласно 3.17):
,
т. е. решаем задачу:
.
Очевидно,
что решением является
.
Шаг
5. Положить
.
и перейти к шагу 1.
Итерация 2
Шаг
1. Для
:
,
.
Шаг
2. 
.
Решаем
задачу
при условиях:
.
Оптимальное
значение этой ЗЛП –
;
.
Шаг
3. Так как
,
переходим к шагу 4.
Шаг 4. Решаем задачу линейного поиска:
.
Определяем :
.
Таким образом, решая задачу
,
получим оптимальное значение
:
.
Шаг
5. Положить:
.
и перейти к шагу 1.
Итерация 3
Шаг
1. Для
:
,
.
Шаг
2. 
.
Решаем задачу
при условиях:
.
Решение:
,
.
Шаг
3. Так как
,
задача решена и
.
На рис. 13.6 проиллюстрирован процесс решения задачи.
